Магнитный поток. Теорема Гаусса для магнитного потока.

Потоком вектора 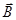(магнитным потоком) через площадку dS называется скалярная величина, равная

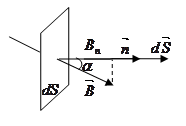
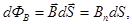
где 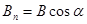- проекция 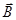на направление нормали к площадке;

a - угол между векторами 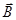и .

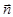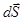- направленный элемент поверхности,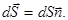

Поток вектора - алгебраическая величина,

если 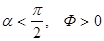- при выходе из поверхности;

если 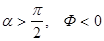- при входе в поверхность.

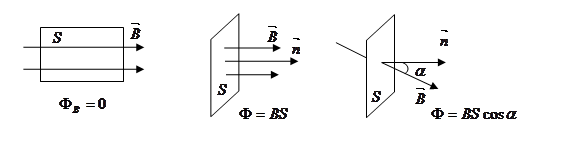
Поток вектора магнитной индукции через произвольную поверхность S равен

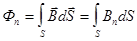
Для однородного магнитного поля =const,

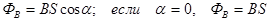
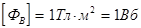
1 Вб - магнитный поток, проходящий через плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.

Магнитный поток через поверхность S численно равен количеству магнитных силовых линий, пересекающих данную поверхность.

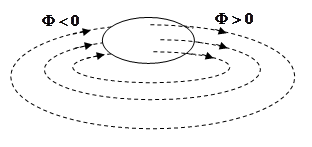
Поскольку линии магнитной индукции всегда замкнуты, для замкнутой поверхности число линий, входящих в поверхность (Ф<0) равно числу линий, выходящих из нее (Ф >0), следовательно, полный поток магнитной индукции через замкнутую поверхность равен нулю.

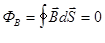- теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Эта теорема является математическим выражением того, что в природе отсутствуют магнитные заряды, на которых начинались бы или заканчивались линии магнитной индукции.