Энергия электростатического поля.

А. Энергия заряженного проводника.

Если имеется заряженный проводник, то его заряд фактически «слеплен» из одноименных элементарных зарядов, т.е. заряженный проводник обладает положительной потенциальной энергией взаимодействия этих элементарных зарядов.

Если этому проводнику сообщить одноименный с ним заряд dq, будет совершена отрицательная работа dA, на величину которой возрастет потенциальная энергия проводника

,

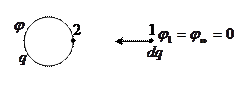
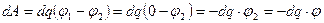где j - потенциал на поверхности проводника.

dW = -dA = dqj

При сообщении незаряженному проводнику заряда q его потенциальная энергия станет равной

,

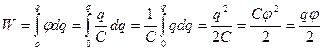т.к. .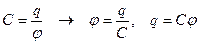

Б. Энергия заряженного конденсатора.

Полная энергия заряженного конденсатора равна той работе, которую надо совершить для его зарядки. Будем заряжать конденсатор, перенося заряженные частицы с одной пластины на другую. Пусть в результате такого переноса к какому-то моменту времени пластины приобрели заряд q, а разность потенциалов между ними стала равной

.

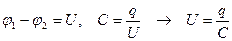Для переноса очередной порции заряда dq необходимо совершить работу

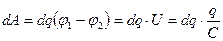
Следовательно, полная энергия, затраченная на зарядку конденсатора

от 0 до q

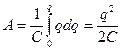
Вся эта работа пошла на увеличение потенциальной энергии:

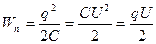(1)

Объемная плотность энергии электростатического поля

Выразим энергию электрического поля конденсатора через величины, характеризующие электрическое поле:

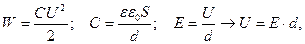
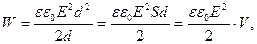(2)

где V = S d - объем, занимаемый полем.

Формула (1) связывает энергию конденсатора с зарядом на его обкладках, формула (2) - с напряженностью поля. Где же локализована энергия, что является носителем энергии - заряды или поле? Ответ вытекает из существования электромагнитных волн, распространяющихся в пространстве от передатчика к приемнику и переносящих энергию. Возможность такого переноса свидетельствует о том, что энергия локализована в поле и переносится вместе с ним. В пределах электростатики бессмысленно разделять энергию заряда и поля, поскольку постоянные во времени поля и обуславливающие их заряды не могут существовать обособленно друг от друга.

Если поле однородно (плоский конденсатор), заключенная в нем энергия распределяется в пространстве с постоянной плотностью.

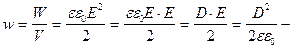объемная плотность энергии.