Внезапное расширение

В случае внезапного расширения потока жидкости местные потери напора и коэффициент сопротивления можно определить теоретически.

Рассмотрим случай, когда трубопровод малого поперечного сечения диаметром 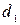резко переходит в большое сечение диаметром 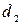. Ось х потока движущейся жидкости по горизонтальному трубопроводу соответствует ее оси. Выделим часть потока между сечениями 1-1 и 2-2 (рис. 4.17). Первое сечение находится на границе расширения трубопровода, и в этом сечении движение будем считать плавно изменяющимся. Второе сечение располагается на некотором расстоянии от первого, в котором не происходит возмущение движения в результате деформации. Эпюра скоростей в сечении 2-2 выравнивается, а поток жидкости будет также плавно изменяющимся.

Поток жидкости, выходящий из малого сечения, поступает в виде транзитной струи в большее сечение трубопровода. В месте внезапного расширения происходит отрыв потока от стенки. В месте отрыва возникает вихревая, водоворотная область, имеющая кольцевую форму. Водоворотная область не участвует в поступательном движении потока. Между водоворотной областью и струей возникает поверхность раздела. Поверхность раздела, в которой происходит интенсивное перемешивание частиц в результате пульсации и возникновение вихрей, неустойчива.

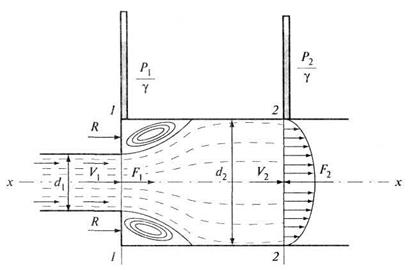
Рис. 4.17. Внезапное расширение

В результате вихреобразования на границе поверхности раздела происходит интенсивный обмен частицами жидкости с транзитной струей. Струя на длине водоворотной области приобретает вращательно-поступательное движение, т.е. появляется окружная составляющая скорости 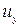. За водоворотной областью вращательное движение прекращается.

Местные гидравлические потери напора возникают между выбранными двумя сечениями в результате отрыва потока от стенок с образованием вихреобразования в виде водоворотной области.

В каждом из сечений площади, скорости и давления обозначим через 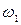, , 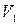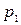(1-е сечение) и , , 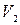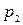(2-е сечение). Так как в сечении 2-2 плавно изменяющееся движение, то гидростатический напор в любой точке сечения постоянен 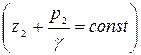. Допускаем, что в сечении 1-1 также гидростатический напор постоянен.

Для определения потерь напора используем уравнение Бернулли для сечений 1-1 и 2-2. Плоскость сравнения проходит по оси трубы:

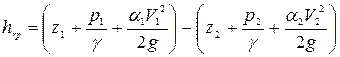, (4.117)

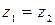принимаем коэффициенты кинетической энергии 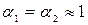, тогда

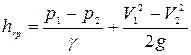. (4.118)

Применим к участку потока, находящегося между сечениями, теорему количества движения (гидравлическое уравнение количества движения). При составлении уравнения силами трения 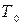со стороны стенок трубы d₂ при условии, что расстояние между сечениями 1-1 и 2-2 сравнительно мало, пренебрегаем, т.е. .

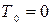Проекция силы тяжести G участка потока на направление движения по оси х .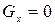

Следовательно, на участок будут действовать только силы гидростатического давления на торцевые живые сечения 1-1 и 2-2 со стороны жидкости, которые находятся перед участком и за ним. Кроме этих сил учитывается реакция вертикальной стенки R. R - сила, приходящаяся на кольцевую площадь между диаметрами труб 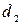и .

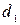Масса жидкости, протекающая через каждое сечение, за время dt

. (4.119)

Изменение количества движения за dt относительно оси х

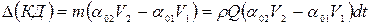. (4.120)

Принимаем коэффициенты количества движения .

Так как давление в сечении подчиняется гидростатическому закону, можно записать, что силы будут равны:

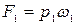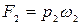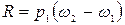; ; . (4.121)

Импульс сил на ось х по направлению движения можно записать в виде

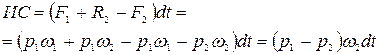(4.122)

Гидравлическое уравнение количества движения 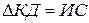. Тогда, приравнивая выражения (4.120) и (4.122), получаем

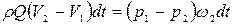. (4.123)

Имея в виду, что

,

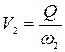находим

. (4.124)

Подставляем (4.124) в уравнение (4.118), получаем

(4.125)

или

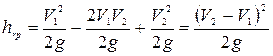. (4.126)

Полученная формула (4.126) называется формулой Борда.

Разность скоростей 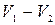носит название потерянной скорости на участке потока при внезапном расширении - . Потери напора при внезапном расширении равны скоростному напору от потерянной скорости и равны

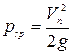. (4.127)

Согласно уравнению неразрывности 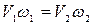, откуда средняя скорость в первом сечении .

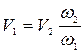Введем в формулу Борда скорость 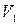через 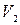и вынесем за скобки 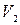, получим

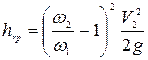. (4.l28)

Обозначим

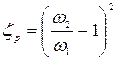. (4.129)

Тогда получим

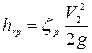, (4.130)

где 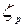- коэффициент местного сопротивления при внезапном расширении потока жидкости.

Следует отметить, что коэффициент 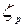был получен теоретическим путем.

Если скорость принять равной 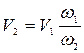, то можно аналогично получить следующую формулу:

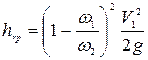, (4.131)

где коэффициент местных сопротивлений

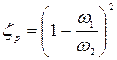. (4.132)

Рассмотрим случай, когда при внезапном расширении 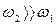, это соответствует выходу потока жидкости в резервуар или бассейн, тогда 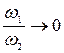и 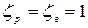( 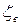- коэффициент местных потерь на выходе).

Гидравлические потери напора в этом случае будут

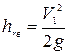. (4.133)

♦ Пример 4.4

При внезапном расширении горизонтального трубопровода средняя скорость в трубе большего диаметра равна 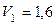м/с.

Отношение диаметров труб 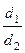. Определить разность показаний пьезометров, установленных до расширения трубопровода, и последнего, пренебрегая и учитывая потери напора (рис. 4.17).

Составим уравнение Бернулли для сечений 1-1 и 2-2. Сечение 1-1 будет находиться до расширения трубопровода, а 2-2 - после расширения. Плоскость сравнения проходит по оси трубопровода, следовательно, .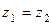

.

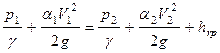Рассматриваем случай, когда потери напора 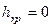. Принимаем условие, что .

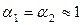Разность показаний пьезометров 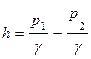, тогда .

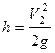Согласно уравнению неразрывности 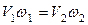, следовательно, скорость

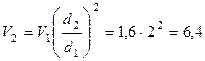м/с;

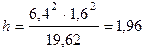м.

В случае учета потерь напора

.

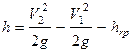Гидравлические потери вычисляются по формуле Борда (4.126):

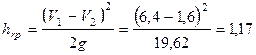м.

Разность показаний пьезометров

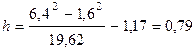м.