Внезапное к. з. синхронных генераторов

Внезапное к. з. – симметричное, происходит при работе на х. х. путем одновременного замыкания всех зажимов статора.

Процесс внезапного к. з. аналогичен к. з. трансформатора (и любой 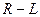цепи переменного тока), но из-за наличия вращающихся частей более сложен.

Точное аналитическое рассмотрение того процесса может быть сделано на базе уравнений Парка – Горева, из-за их сложности мы будем рассматривать процесс иначе, в 2 этапе.

1) определим начальные значения токов, положив, ;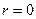

2) рассмотрим закономерности изменения этих токов.

При анализе примем следующие допущения:

1) обмотка возбуждения ( 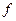) и успокоительная (y) приведены к обмотке якоря (т.е. заменены эквивалентными приведёнными 3-фазными обмотками, расположенными на якоря и образующие в зазоре такое же поле, что и реальные обмотки);

2) n – в процессе к. з. не успевает измениться, т. е. n=const

3) ;

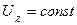4) 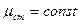, т. е. насыщение магнитной цепи не меняется;

Начальные токи к. з.

Поскольку активные сопротивления обмоток малы по сравнению с индуктивными, то на начальные токи к. з. они не влияют, а лишь вызывают затухание свободных токов. Поэтому на данном этапе будем считать, что все обмотки сверхпроводящие, т. е. r = 0.

Теорема о постоянстве потокосцепления.

Если электрическая цепь не содержит источников э.д.с., то она описывается дифференциальным уравнением:

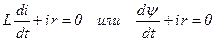
(7.2.1)

где 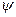− полное потокосцепление этой цепи, обусловленное потоками как собственной, так и взаимоиндукции. Если 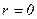, то (7.2.1) принимает вид:

, => .

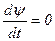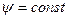(7.2.2)

Потокосцепление сверхпроводящей электрической цепи остается постоянным.

Если к такой, цепи поднести магнит, то в ней будет индуктироваться ток такой величины и знака, что создаваемое этим током потокосцепление будет полностью компенсировать 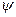, вызванное приближением магнита.

Пусть к. з. произошло на холостом ходу (синхронный генератор работает автономно).

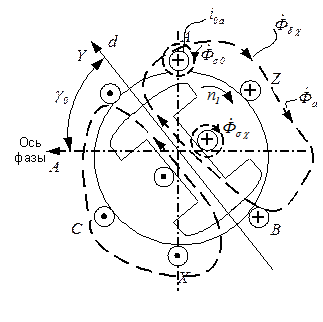
Рисунок 7.2.2 – Поле обмотки возбуждения

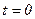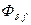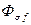Картина поля обмотки возбуждения для (начальный момент к з.) показана на рисунке (7.2.2). и − соответственно основной поток и поток рассеяния обмотки возбуждения. 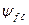− максимальное потокосцепление фазы с основным потоком возбуждения.

Вектор 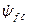(пространственный) совпадает по фазе с осью d (потоком 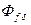). Если ось обмотки фазы совпадает с осью d , то потокосцепление фазы с 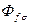максимально и равно 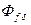. Для произвольного положения оси d 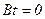потокосцепление фаз определяется проекцией фазы, т. е.

;

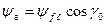(7.2.3)

;

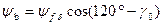(7.2.4)

.

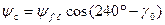(7.2.5)

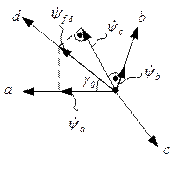
Рисунок 7.2.3 – Пространственная векторная диаграмма потокосцеплений обмотки якоря в начальный момент к.з.

Согласно упомянутой теореме при 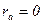для каждой фазы 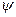должно оставаться постоянным и при 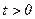. Следовательно, должны возникнуть такие токи, которые создают 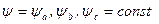(во времени). Это – только апериодические постоянные токи , , .

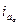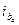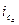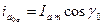,	(7.2.6)
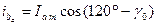.	(7.2.7)
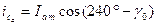.	(7.2.8)

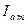− наибольшее возможное значение апериодического тока ( 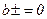ось фазы совпадает с осью d)

Рисунок 7.2.4 – Пространственная векторная диаграмма потоков обмотки якоря в начальный момент к.з.

Апериодические токи якоря создают результирующий поток 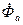неподвижный в пространстве который создаёт с обмотками 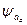, , 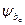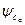− поддерживающие постоянство 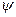. 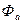совпадает по фазе с 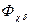. Поскольку принято, ч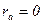то , то 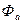неизменен во времени.

Однако ротор продолжает вращаться с синхронной скоростью, и поток 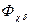создает с фазами переменные потокосцепления. Для их компенсации необходимо , чтобы в фазах якоря возникла система 3-фазных периодических токов, создающая результирующий поток 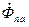, вращающийся синхронно с роторам направленный навстречу с 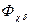. Амплитуда периодического ток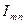а равна 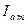. А для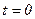 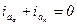(т. к. предвключенный режим х.х.)

С другой стороны периодические токи якоря можно рассматривать как переменные токи к. з. в установившемся режиме. Т. к. мы положим, что 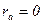, то эти токи – чисто индуктивные, создающие размагничивающий поток рассеивания, что и надо для соблюдения теоремы о постоянстве потокосцеплений.

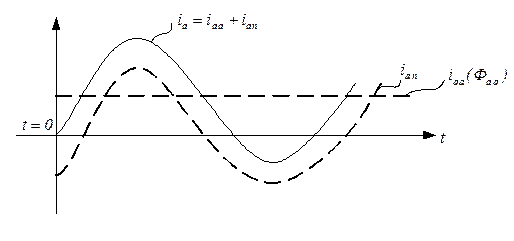
Рисунок 7.2.5 – Составляющие токов к.з. обмотки якоря

Токи в обмотках возбуждения и успокоительной.

Т. к. поток 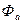неподвижен в пространстве, а ротор вращается переменный, ток основной частоты 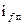и 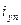. Эти токи чисто индуктивные ( 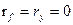) и по правилу Ленца создают поток 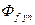вращающийся относительно ротора и неподвижный относительно статора, направленный навстречу .

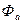Опять нарушается теорема о постоянстве 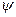для якоря и ротора. Поэтому в обмотке возбуждения в успокоительной обмотки возникают всплески токов 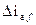и 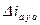направленные согласно с .

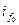Если бы не было потоков рассеяния, которые также участвуют в сохранении постоянства потокосцепления, то токи обмоток росли бы до бесконечности по схеме ( 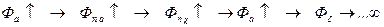) но рост токов ограничивается ростом 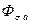и .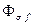

Для обмотки возбуждения и успокоительной обмотки:

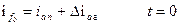,	(7.2.9)
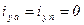.	(7.2.10)

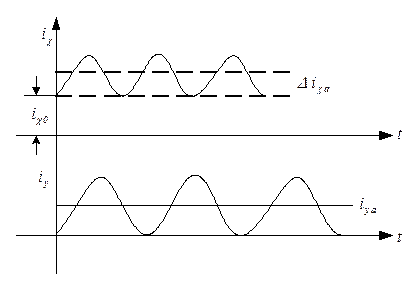
Рисунок 7.2.6 – Составляющие токов к.з. обмотки возбуждения

На самом деле 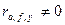и апериодические токи будут затухать.

Токи внезапного к. з.

Для расчета токов к. з. используем теорему о постоянстве потокосцепления обмоток, принимая, что в общем случае синхронный генератор имеет три обмотки: якоря, возбуждения и успокоительную. Потокосцепление любой обмотки

,

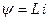(7.2.11)

где L – суммарная собственная и взаимная индуктивность обмотки.

Положим, что к. з. произошло на холостом ходу и 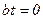ось фазы (пусть А) совпадает с осью d.

Будем также учитывать, что процесс взаимной индукции друг с другом связаны:

1) апериодические токи статора и периодические токи ротора;

2) периодические статора и апериодические ротора;

1-е уравнение определяет периодическое потокосцепление фазы статора, ось которой совпадает с осью d при t = 0.

,

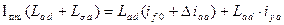(7.2.12)

Эти 3 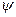должны в сумме давать ноль, т. к. постоянство начального 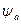обеспечивается апериодическими токами и .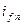

2-е уравнение для обмотки возбуждения:

,

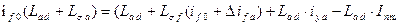(7.2.13)

3-е уравнение – для успокоительной обмотки:

.

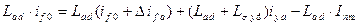(7.2.14)

Для каждой из обмоток потокосцепления самоиндукции определяется 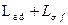, а взаимоиндукции – 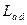. Если все уравнения умножить на 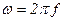, принять 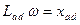; ; 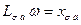; 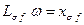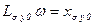. 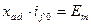− амплитуда э. д. с., индуктируемой ВОЯ током .

.

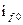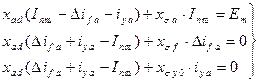(7.2.15)

Система уравнений (7.2.15) соответствует схема замещения, показанная на рисунке (7.2.7).

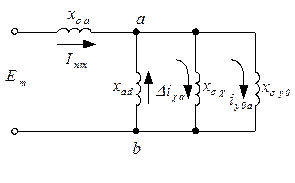
Рисунок 7.2.7 – Схема для сверхпереходного сопротивления по продольной оси

1-е уравнение – контур ;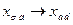

2-е − ;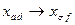

3-е − ;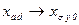

Из схемы видно, что

,

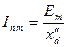(7.2.16)

т. е. определяется сопротивлением 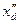равным

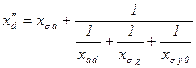
(7.2.17)

− продольное сверхпереходное индуктивное сопротивление обмотки якоря.

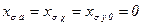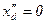Из (7.2.16) видно, что, если рассеяния нет, т. е. , то и 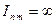, что ранее было показано физически.

Величина тока внезапного к. з. ограничивается только сопротивлениями рассеяния обмоток.

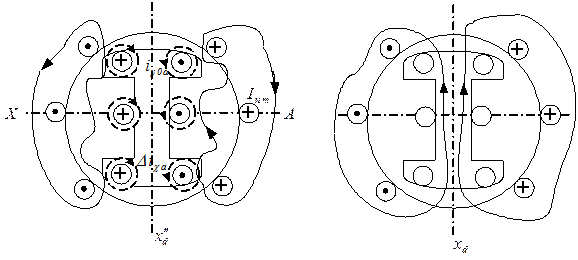
Рисунок 7.2.8 – Влияние успокоительной обмотки на распределение потоков

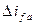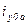Из рисунков следует также, что в результате действия токов и поток якоря через воздушный зазор вытесняется на пути потоков рассеяния обмоток ротора и из-за большего магнитного сопротивления этого пути поток якоря, создаваемый одним и тем же током сильно уменьшается.

Решение системы (7.2.15) относительно токов ветвей даёт следующие результаты: 1. направление между зажимами a и b

;

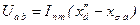(7.2.18)

2. апериодический ток в обмотках возбуждения

;

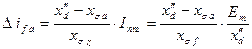(7.2.19)

3. апериодический ток в успокоительной обмотке

.

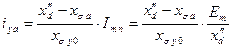(7.2.20)

Если успокоительная обмотка отсутствует, то 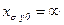, а схема упрощается.

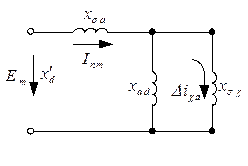
Рисунок 7.2.9 – Схема для переходного сопротивления по поперечной оси

Сопротивление этой схемы

.

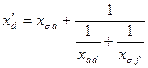(7.2.21)

называется продольным переходным индуктивным сопротивлением обмотки якоря.

Из схемы рисунок (7.2.9) видно, что 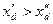, т. е. 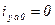и поток реакции якоря вычитается только на пути потоков рассеивания обмотки возбуждения.

Наличие успокоительной обмотки приводит к увеличению токов внезапного к. з.

Однако при этом уменьшается 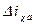. Из схемы значение периодического якоря равно:

,

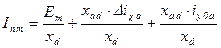(7.2.22)

т. е. периодический ток якоря имеет три составляющие:

1) установившаяся, т. е. при t = 0,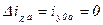

,

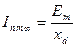(7.2.23)

2) ток, индуктируемый в якоре током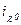

,

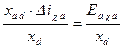(7.2.24)

3) ток индуктируемый в якоре током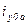

,

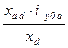(7.2.25)

Если активные сопротивления обмоток равны нулю, то

.

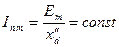(7.2.26)

На самом деле 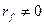, поэтому ток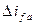и и 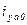затухают до 0 и 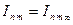. Разность

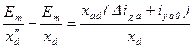
(7.2.27)

затухает соответственно затуханию токов 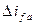и .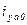

Можно показать, что при замкнутой обмотке якоря 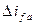и 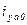имеет по две составляющие, затухающие с 2-мя постоянными времени:

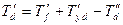,	(7.2.28)
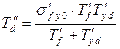,	(7.2.29)

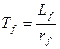,	(7.2.30)
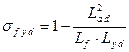.	(7.2.31)

Исследуемая разность затухает тоже

,

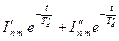(7.2.32)

причем

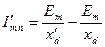;	(7.2.33)
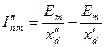.	(7.2.34)

Текущее значение тока якоря определяется:

,

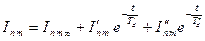(7.2.35)

Мгновенное значение периодического тока:

,

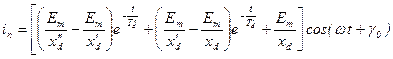(7.2.36)

где 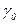− начальная фаза тока к. з.

Апериодический ток якоря, если 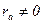затухает с постоянной времени 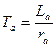, 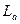− эквивалентная индуктивность обмотки якоря.

Апериодический поток 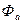изменяться относительно осей d и q и индуктирует переменные токи в поперечной успокоительной обмотки.

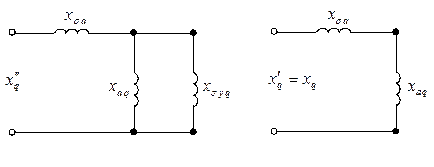
Рисунок 7.2.10 – Схема для сверхпереходного сопротивления по поперечной оси

,

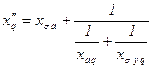(7.2.37)

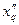− поперечное сверхпереходное индуктивное сопротивление обмотки якоря;

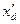− поперечное переходное индуктивное сопротивление;

Если машина явнополюсная и 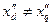, то величина апериодического тока якоря пульсирует с двойной частотой, т. к. при уменьшении индуктивности так должен возрастать для поддержания постоянства потокосцепления.

,

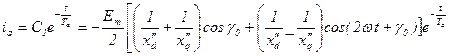(7.2.38)

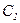определяется из условия, что при t = 0 => .

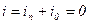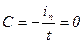Если апериодический ток максимален, то пик тока достигает своего максимально возможного значения, называемого ударным током к. з.

Если затухания нет, то

.

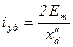(7.2.39)

В соответствии с ГОСТ − 183 − 66 принято

,

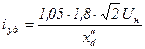(7.2.40)

( дополнительная работа при ).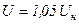

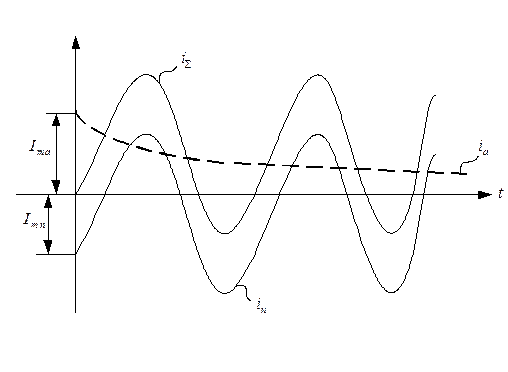
Рисунок 7.2.11 – Мгновенные значения тока внезапного короткого замыкания

Действие токов к. з.

Тепловое действие токов неопасно, так как тепловая система – инерционна, а защита быстро отключает повреждение. Весьма опасны электродинамические усилия, которые действуют главным образом на любые части обмоток и пропорциональны 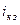. поэтому требуется надёжное крепление лобовых частей.

Электромагнитный момент – постоянная составляющая отсутствует, так как ток практически чисто реактивный (поле статора и обмотка возбуждения вращаются синхронно на встречу, друг другу и взаимодействуют).

Основной момент – от взаимодействия токов ротора с апериодическим током статора – носит пульсирующий характер (машина находится в режиме вынужденных колебаний).

Если к. з. происходит на выбеге т. е. при отсутствии момента приводного двигателя, то скорость ротора будет уменьшаться и испытывать колебание.

Ударный генератор

Капица П. Л. В 1924 г. находился на стажировке в Кавендшиской лаборатории у Резерфорда. Для изучения некоторых физических явлений ему нужны были сильные магнитные поля. Он использовал соленоид, питаемый от АБ, но мог получить лишь 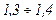кА. Этого было мало. Новый источник: быстроходный синхронный генератор, его рабочий режим – к. з. В момент к. з. при прохождении тока через обмотку статор замыкается специальным механическим выключателем и размыкается через 0,01с (1/2 периода). Это во 1-х позволяет получить 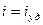, а во-вторых – производить коммутацию при 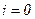и избежать дуги.

В этом синхронном генераторе 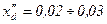(в обычных ).

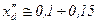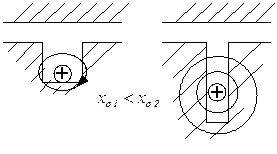
Рисунок 7.2.12 – Конструкция паза якоря ударного генератора

Для получения малых 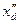делают 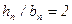(обычно 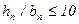) и для уменьшения 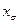экранируют обмотку статора для демпфирования полей рассеяния (латунь, бронза – ещё и крепят лобовые части).

Ротор – максимальный , .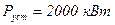

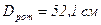Для уменьшения 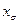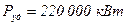, 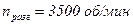. Разгонялся ДПТ (80 л. с.)