Четвертая нормальная форма

Известно, что каждое отношение r(R), удовлетворяющее MV-зависимости XààY, разлагается без потерь на отношения со схемами XY и XZ, где Z = R—(XY). Однако если ХààY единственная зависимость в R, то R находится в 3НФ. Таким образом, 3НФ не определяет все возможные декомпози­ции.

MV-зависимость XààY называется тривиальной для схемы R, содержащей XY, если любое отношение r(R) удовлетворяет XààУ.

Пусть F — множество F- и MV-зависимостей над U. Схема отношения R≤U находится в четвертой нормальной форме (4НФ) относительно F, если для каждой MV-зависимости XààY, выводимой из F и XY 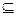R либо MV-зависимость тривиальна, либо X является суперключом для R. Схема БД R находится в 4НФ относительно F, если каждая входящая в нее схема отношения находится в 4НФ относительно F.

Пример 3.15. Пусть R(ЗАВОД ТОВАР МАГАЗИН) — схема отношения и пусть F= {ЗАВОДààТОВАР}, R не находится в 4НФ относительно F. Схема БД R (ЗАВОД ТОВАР, ЗАВОД МАГАЗИН) находится в 4НФ относительно F, поскольку каждое отношение r(R), удовлетворяющее F, разлагается без потерь по схемам из R.

Заметим, что 4НФ является обобщением НФБК. Когда F включает только F-зависимости (если R нахо­дится в 4НФ), то оно будет в НФБК. В этом случае XààY означает XàY. Предположим, что R не находится в НФБК, так как существует некоторая F-зависимость ХàA, где X не содержит никакого ключа. Если XA =R, то, без сомнения, X включает какой-либо ключ. Следовательно, ХА не включает всех атрибутов и отсюда следует нарушение 4НФ F-зависимостью ХàА, представляющей собой специальный случай MV-зависимости ХààУ.

Схему отношения R, обладающую свойством соединения без потерь относительно множества F F-зависимостей и MV-зависимостей, можно разложить на несколько схем отношений R_i, каждая из которых находится в 4НФ. Для этого, начиная с R, ищем выводимую из F нетривиальную MV-зависимость XààY, для которой X не является ключом R. Далее R разлагаем на два отношения R₁ = XY и R₂ = XZ, где Z = R—(XY). MV-зависимость XàY теперь тривиальна в R₂ и неприложима к R₂. Про­цесс декомпозиции повторяем для той из схем R₁ и R₂, которая не находится в 4НФ относительно F. Поскольку используемые MV-зависимости не являются тривиальными, обе возникающие реляционные схемы содержат меньше атрибутов, чем исходные. Таким образом, процесс декомпозиции обязательно заканчивается.

Пример 3.16. Пусть F={AààBCD, BààAС, СàD} — мно­жество зависимостей над схемой R(A, В, С, D, Е, I). Поскольку АààВСD является нетривиальной MV-зависимостью и при этом А не есть ключ R, разлагаем R на схемы отношений R₁(A, В, С, D) и R₂(A, Е, J). Схема R₂ находится в 4НФ относительно F. Из F выте­кает MV-зависимость ВààАС на R, но она не может быть исполь­зована в декомпозиции, поскольку, в силу CàD, В есть ключ для R₁. Однако из CàD следует MV-зависимость СààD, которую можно использовать в декомпозиции R₁. В результате получаем схемы от­ношений R₁₁(A, В, С) и R_l2(C, D). Обе схемы находятся в 4НФ отно­сительно F. Таким образом, схема БД R=(R₁₁, R₁₂, R₂) находится в 4НФ относительно F.

* * *

Проектирование реляционных БД преследует две основные цели: снизить избыточность данных и повысить их надежность. В процессе проектирования БД требуется выбрать из множества альтернативных схем те, которые потенциально не обладают недостатками выполнения операций включения, замены, удаления кортежей. Для достижения указанных целей используют ограничения, накладываемые на совокупности данных, центральное место среди которых отводится зависимости данных.

Функциональные зависимости и ЗНФ, а также аксиомы F-зависимостей явились основой исследований и разработок проектирования реляционных БД. Как было показано, при заданном множестве F-зависимостей F над R можно найти схему БД в ЗНФ, удовлетворяющую F. Для НФБК это неверно, т. е. множество F-зависимостей может не иметь полной НФБК схемы БД.

Присутствие в реляционной схеме F-зависимостей еще не означает возможности декомпозиции схемы, позволяющей уменьшать избыточность и ликвидировать недостатки операций запоминания. Поскольку ЗНФ не опре­деляет все возможные декомпозиции отношения, удовлетворяющего MV-зависимостям, то была введена 4НФ схемы отношения. При помощи аксиом F- и MV-зависимостей, исходя из F, можно получить полное множество таких зависимостей. MV-зависимости являются специальным случаем зависимости соединения, где от соединения n отношений для n≥2 требуется, чтобы оно было соединением без потерь.