Способы задания отношений

По определению отношения R между элементами множества Х есть всякое подмножество декартова произведения Х ´ Х, т.е. множество, элементами которого являются упорядоченные пары. Поэтому способы задания отношений, по существу, такие же, как и способы задания множеств.

Отношение R на множестве Х можно задать, перечислив все пары элементов, взятых из множества Х и связанных этим отношением.

Формы записи при этом могут быть различными. Например, некоторое отношение R на множестве Х = {4, 5, 6, 7, 9}можно задать, записав множество пар: {(5,4),(6,4),(6,5),(7,4),(7,5),(7,6),(9, 4),(9,5),(9,6),(9,7)}.То же отношение можно задать при помощи графа.

Отношения на конечном множестве Х можно представлять наглядно, при помощи особых чертежей, состоящих из точек, соединенных стрелками. Такие чертежи называют графами.

Построим граф отношения «меньше», заданного на множестве Х = {2, 4, 6, 8}. Для этого элементы множества Х изобразим точками (их называют вершинами графа), а отношение «меньше» – стрелкой.

2• • 4

8 · · 6

Пример

На том же множестве Х можно рассмотреть другое отношение – «кратно». Граф этого отношения будет в каждой вершине иметь петлю (стрелку, начало и конец которой совпадают), так как каждое число кратно самому себе.

2 · · 4

8 · · 6

Чаще отношение R на множестве Х задают, указав характеристическое свойство всех пар элементов, находящихся в отношении R. Это свойство задается при помощи предложения с двумя переменными.

Пример. Пусть заданы рассмотренные выше отношения «меньше» и «кратно», причем использована краткая форма предложений«число х меньше числа у» и «число х кратно числу у». Некоторые такие предложения можно записать используя символы. Например, отношения «меньше» и «кратно» можно было записать в таком виде: «х < у», «х 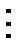у». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или х – у = 3). Отношение между прямыми плоскости задают, используя символы: х // у, х ^ у.

Для отношения R, заданного на множестве Х, всегда можно задать отношение R ^-1 , ему обратное. Например, если R – отношение “х меньше у”, то обратным ему будет отношение “ у меньше х”.

Понятием отношения, обратного данному, часто пользуются при начальном обучении математике. Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?» – ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?». Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2».