Инженерно-геодезические опорные сети
Предмет и задачи прикладной геодезии
1. Предмет ПГ является метод производства топографо-геодезических работ для решения инженерных задач в различных отраслях экономики. Основными задачами ПГ являются:
1) разработка основных программ инженерного обеспечения строительство, эксплуатации и кадастра всех типов сооружений (например: схема геодезического обеспечения многоэтажных зданий отлична от схемы геодезического обеспечения зданий коттеджной застройки);
2) создание приборной базы геодезического обеспечения (наример: при переносе вертикальных осей с этажа на этаж - на верхние этажи необходимо оптические приборы и оптические отвесы, т. к. нитяные коротки и неудобны, а поскольку вертикальные оси должны быть ещё и видимы, то приборы задающие луч должны быть еще и лазерами)
2. Основными частями геодезических работ и курса являются:
1) топографо-геодезические изыскания строительных площадок
2) инженерное геодезическое проектирование сооружений;
3) разбивочные работы;
4) геодезическая выверка конструкций и технического оборудования;
5) наблюдение за деформацией сооружений.
Топографо-геодезические изыскания строительных площадок - съёмки. Инженерное геодезическое проектирование сооружений - проектирование сооружений осуществляется на основе топографических планов. На основе оптимального варианта проекта готовят проект выноса в натуру основных осей будущего сооружения. Проект сводится к подготовке разбивочного чертежа, как в плане, так и по высоте. Разбивочные работы - вынос в натуру.
3. Проектная документация делится на несколько частей в зависимости от стадий проектирования. Основные стадии: 1) технико-экономическое обоснование строительства, 2) рабочие чертежи. На 1ой стадии применяются карты и планы масштабов от 1:5000 до 1:25000. На 2ой стадии, где даны проекты составных частей сооружений, необходимы планы масштабов 1:2000 и крупнее до 1:500.
4. Проект производства геодезических работ при строительстве соответствует проекту производства работ по самому строительству. Например, проект производства геодезических работ состоит из 1) сооружения фундамента; 2) сооружения колон; 3) стен; 4) перекрытия; 5) крыша. На каждый этап и составляется проект производства геодезических работ. Проект производства геодезических работ составляется отделом главного маркшейдера.
Инженерно-геодезические опорные сети
1. Назначение: эти сети являются основой для выполнения комплекса проектно-изыскательных и строительных работ. Они могут выполняться как в системе координат ГГС, так и в местной системе координат. Методами построения плановых геодезических сетей являются: триангуляция, полигонометрия, сети глобальных позиционных систем, строительные сетки. Особенность построения этих сетей является: 1) высокая точность определения положения опорных пунктов, 2) короткие длины сторон, 3) высокая требовательность к центрированию приборов, 4) влияние сооружений на точность производства работ. Данные по точности: для крупных городов СКО положения опорного пункта должна быть меньше 5 см, базовый масштаб съемки 1:500; райцентры - 10 см, 1:1000; др. населенные пункты - 15 см, 1:2000.
2. Главный принцип проектирования и построения плановых сетей - от общего к частному. Этот принцип соответствует принципу проектирования строительства, так на стадии ТЭО проектирование делается в общем и точность к расположению главных осей сооружений может быть не высокой. На общей стадии соответствующей ТЭО точность выноса в натуру может быть низкой, однако точность выноса в натуру на стадии рабочих чертежей должна быть высокой и обеспечивать технологическую эксплуатацию сооружений. Именно этой высокой точности определяется точность опорной геодезической сети.
Согласно пособию «Левчук. Прикладная геодезия» с. 22. приведем метод расчета точности опорных сетей и количество ступеней их развития.
Будем считать, что на положение пункта i-той ступени влияет два факта:
1) СКО положения пункта i-1 ступени;
2) влияние СКО измерений i-той ступени mui - СКО в положении пункта i-той ступени, вызванная ошибкой измерений
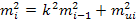
mi - СКО положения пункта i-ступени
mi-1 - СКО положения пункта i-1 ступени
mui - составляющая СКО mi вызванная ошибкой измерений в i-той ступени
Тогда полагаем наличия ряда ступеней
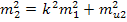
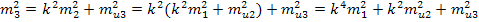
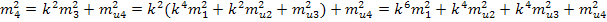
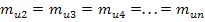
n - число ступеней
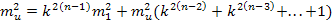
Если n ступеней, то число членов геометрической прогрессии n-1
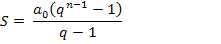

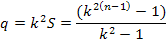
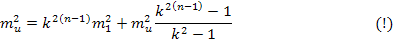
Обычно все геодезические построения привязываются на своих концах к опорным пунктам. В таких случаях k=0.7. Если привязка на 1 пункте, то k=1. Исследуем, как влияет ошибочность самой первой ступени на точность n-ой ступени.
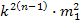
Возьмем
n=3 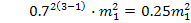
n=4 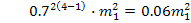
Влиянием ошибки не пренебречь, если оно составляет 0,3 результирующей ошибки или квадрат СКО <0.32результирующей СКО.
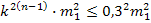
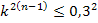
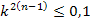
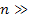 3
3
Только третья предыдущая ступень влияет на точность этой ступени. В уравнении задаваясь одними величинами можно вычислить другие. Выражение справедливо для случаев, когда их дирекционные углы безошибочны. Если ошибкой дирекционных углов пренебречь нельзя, то их учитывают. В самом неблагоприятном случае дисперсии исходных дирекционных углов увеличение дисперсии положения пункта в последующей ступени в 2 раза. Тогда функция влияния ошибки
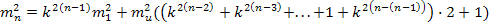
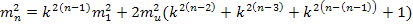
В 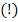 имеется неопределенность при
имеется неопределенность при 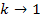
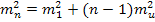
2.1. Расчет точности проекта геодезической сети
Часто на инженерных объектах одноступенчатые сети. Задача проектирования ставится так: задан проект геодезической сети на карте, задана СКО положения определения пункта относительно исходного в наиболее слабом месте или ошибка взаимного положения пунктов. Требуется рассчитать точность угловых и линейных измерений или GPS- измерений в данной геодезической сети, чтобы по критерию точности она удовлетворяла приведенным требованиям.
Существует два критерия:
1) СКО взаимного положения пунктов в наиболее слабом месте сети.
2) СКО положения пункта в наиболее слабом месте сети относительно опорных пунктов
Решаем задачу по первому критерию. В основе решения примем выражение матрицы определяемого пункта при параметрическом способе уравнивания.
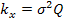
σ- стандарт измерений, которым приписывается вес единицы
Q – обратно- весовая матрица определения пунктов, N-1 обратная к N - матрице нормальных уравнений.
Порядок решения:
1) по схеме сети определяют матрицу уравнений поправок и задаются веса измерений:
угловым - 1; линейным - 0,6; 0,3 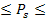 3
3
2) составляют матрицу нормальных уравнений N=AͬРА
3) находят обратную матрицу N-1= Q
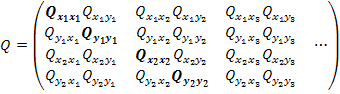
Диагональные элементы – это обратно весовые коэффициенты координат определяемых пунктов после уравнивания.
4) СКО положения i-того пункта
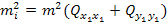
Находим:
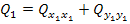
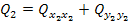
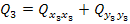
………………………………
5) находим
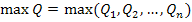
6) задаваясь по инструкции СКО положения пункта в наиболее слабом месте 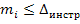 , записываем исходя из выражения
, записываем исходя из выражения 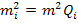 , что
, что
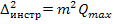
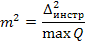
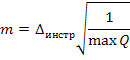
Мы предрассчитали точность измерений, вес которых принимается равным 1, т.е. измерения со СКО 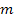 . Но у нас имеются и другие измерения, например, линии. Их точность определяется исходя из соотношения весов. Например, пусть задана величина
. Но у нас имеются и другие измерения, например, линии. Их точность определяется исходя из соотношения весов. Например, пусть задана величина 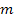 , для которой р=1,
, для которой р=1, 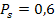 . Необходимо найти
. Необходимо найти 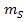 . Тогда запишем известное соотношение весов
. Тогда запишем известное соотношение весов
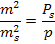
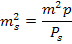
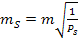 ,
,
Что соответствует задаваемой по проекту средней квадратической ошибке линейных измерений.
Дадим особое решение этой задачи для второго критерия. Второй критерий заключается в заданной СКО взаимного положения пунктов.
Взаимное положение пунктов можно представить следующими векторами:
∆х = х2 – х1,
∆у = у2 – у2;
или
∆=Ах,
где
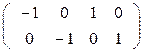 |
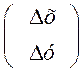
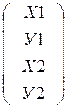 А = , х = , ∆ =
А = , х = , ∆ =
∆ - вектор взаимного положения пунктов.
Найдем корреляционную матрицу этого вектора
К∆ = σ2· АКАт,
где σ –стандарт измерения, вес которого принимается равным единице.
Для этого вначале найдем произведение АК:
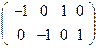 |
АК= ·К =
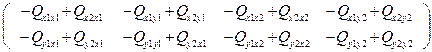 |
=
и окончательно
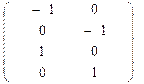 |
σ2· AКАт = σ2· AК · ,
или
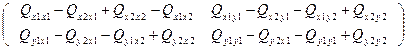 |
К∆ = σ2·
Выведенная матрица характеризует точность взаимного положения пунктов. Для упрощения расчетов на стадии проектирования можно принять недиагональные элементы настоящей матрицы равными нулю (Qх1х2 = Qх2х1 = 0, Qу2у1 = Qу1у2 = 0).
Тогда в упрощенном виде корреляционная матрица взаимного положения пунктов примет вид:
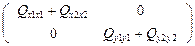 |
К∆ = АКАт = σ2 * ,
где Qх1х1 – это обратный вес положения точки 1 по оси х; Qх2х2 – это обратный вес положения точки 2 по оси х; Qу1у1 – это обратный вес положения точки 1 по оси у; Qу2у2 – обратный вес положение точки 2 по оси у.
Настоящая матрица неудобна для практического применения, где точность взаимного положения выражают одним числом. При этом часто находят сумму диагональных элементов этой матрицы и ею характеризуют точность взаимного положения пунктов, то есть записывают следующее выражение
σ∆ = σ2(Qх1х1+Qч2ч2+Qy1y1+Qy2y2),
где σ∆ - стандарт взаимного положения
Введя обозначения
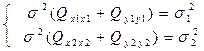
,
где σ1 σ2 – стандарты положения пунктов.
записывают
σ∆ = σ21 + σ22.
Если же принять
σ1 = σ2 = σt ,
тогда
σ2∆ = 2σ2t
Из этого следует, что квадрат стандарта взаимного положения пунктов равен двум квадратам стандарта положения одного пункта Здесь и в дальнейшем будем считать, что средняя квадратическая ошибка и стандарт – одно и то же понятие.
Очевидно, что
σ∆ = σt*√2.
Если в нормативном документе задано максимальное значение для σ∆,
то по нему находится
σt=σ∆/√2,
которое приравнивается к 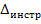 и все расчеты выполняются так, как описано для
и все расчеты выполняются так, как описано для
критерия СКО взаимного положения пунктов в наиболее слабом месте сети
3. Система координат принимается в зависимости от вида инженерных сооружений. Выбирают такую систему, чтобы можно было не вводить поправки за переход в картографическую проекцию. Если взять проекцию Гаусса-Крюгера, то рекомендуется выбирать ширину зоны порядка 20 км влево и вправо от осевого меридиана условной местной системы координат. Иногда подбирают такую систему координат, чтобы суммарная поправка за переход на эллипсоид и в картографическую проекцию была равна 0.
При переходе с земной поверхности S на эллипсоид длина S укорачивается не величину ΔS.
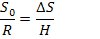
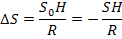
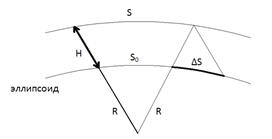
При переходе в картографическую проекцию (ГК) длина линии увеличивается
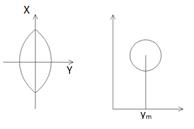
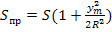
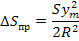
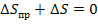
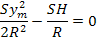
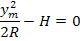
H=200 м, R=6371000 м.
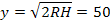
4. Из функции 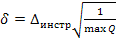 непосредственно вычисляем СКО измерений направлений в триангуляции.
непосредственно вычисляем СКО измерений направлений в триангуляции.
5. Оценку проекта покажем на примере. Пусть создан проект следующей полигонометрической сети. A, B, C, D - исходные. I, II - определяемые.
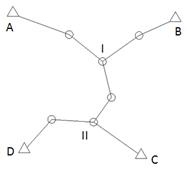
Необходимо рассчитать точности определения положения проектных пунктов I, II, сравнить эту точность с заданной по инструкции или по проекту. Если эта точность недостаточна, то увеличивается, то увеличивается точность угловых и линейных измерений до получения необходимой точности определения пунктов.
Порядок работы следующий: по каждому звену A-I, B-I, D-II, C-II, I-II рассчитать СКО
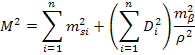
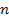 - число сторон в звене
- число сторон в звене
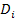 -расстояние от центра тяжести звена к пунктам
-расстояние от центра тяжести звена к пунктам
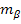 - СКО измерения углов
- СКО измерения углов
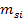 - СКО i-ой стороны
- СКО i-ой стороны
Если принять 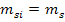
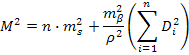
Порядок расчета:
Первое приближение. Вычисление СКО положения точки I по звеньям
mz1 → A-I
mz2 → B-I
mz2 → II-I
при заданных 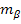 и
и 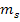 .
.
Вычисляют веса 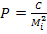 . С - произвольная величина, соразмерная со среднем значением mz, принимаемая для удобства вычислений.
. С - произвольная величина, соразмерная со среднем значением mz, принимаемая для удобства вычислений.
PI = Pz1 + Pz2 + Pz3
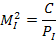
В этом же приближении вычисляют СКО по звеньям относительно точки II
mz4 → С-II
mz5 → D-II
mz6 → I-II
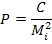
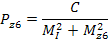
PII = Pz4 + Pz5 + Pz6
Второе приближение. Снова вычисляют
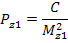
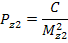
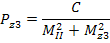
PI = Pz1 + Pz2 + Pz3
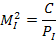
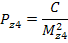
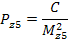
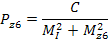
PII = Pz4 + Pz5 + Pz6
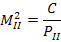
Приближение выполняют до тех пор, пока в двух последних приближениях погрешности не станут равными
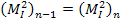
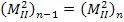
Значения 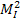 и
и 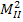 сравниваются с заданным значением
сравниваются с заданным значением
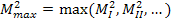
Если 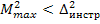 , то проект сети удоавлетворяет заданной точности. Если
, то проект сети удоавлетворяет заданной точности. Если 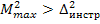 , то нужно дать предложения в проекте по повышению точности измерений.
, то нужно дать предложения в проекте по повышению точности измерений.
6. При построении высотных сетей решается два вопроса:
1) выбор системы высот,
2) расчет точности проектов нивелирных сетей. На основе этих назначается методика нивелирования. Поскольку инженерные объекты по размерам относительно не большие, то применяется метрическая система высот. Из курса теоретической фигуры Земли известно, что существуют следующие системы высот: ортометрическая, нормальная, динамическая. Относительно больших инженерных сооружений, связанных гидротехническим строительством применяется динамическая система высот.
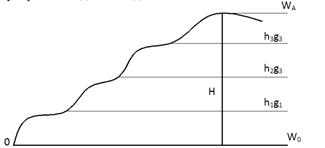
Если принять 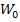 - исходный уровень (уровень исходного потенциала), то высота точки А в динамической систем высот
- исходный уровень (уровень исходного потенциала), то высота точки А в динамической систем высот
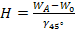
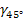 - значение нормальной силы тяжести на
- значение нормальной силы тяжести на 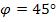
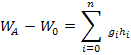
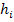 - превышение на станции при нивелировании
- превышение на станции при нивелировании
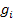 - значение силы тяжести на станции
- значение силы тяжести на станции
При таком подходе высоты водной поверхности водохранилища будут иметь одинаковое значение. Если Н=Σh, то высоты водной поверхности будут различны. По экспериментальным данным отклонение высоты составляет 0,2 м на расстояние 300 км.
Расчет точности проекта нивелирных сетей выполняется точно также, как и полигонометрических, но 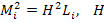 - СКО суммы превышений на 1 км хода, L - длина хода. Если
- СКО суммы превышений на 1 км хода, L - длина хода. Если 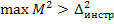 , то нужно повысить точность нивелирования или укорачивать длины ходов.
, то нужно повысить точность нивелирования или укорачивать длины ходов.
7. GPS построения напоминают полигонометрические, нивелирные. Если в нивелирных измеряют превышения, то в GPS приращения ∆Х, ∆Y, ∆Z. Для приближенного расчета проектов можно применять методику, выведенную нами для полигонометрии только для различных осей ∆х, ∆у, ∆z. Если приращения координат осуществляются в местной системе координат
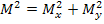 .
.
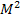 сравнивают с
сравнивают с 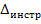 . Если больше, то необходимо повышение точности, но методы оценки проекта способом приближений являются приближенные, не строгие. Самым строгим и общим является метод, базирующийся на параметрическом способе уравнивания
. Если больше, то необходимо повышение точности, но методы оценки проекта способом приближений являются приближенные, не строгие. Самым строгим и общим является метод, базирующийся на параметрическом способе уравнивания
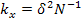 по одному из критериев: 1) СКО положения пункта относительно исходного, 2) СКО взаимного положения пунктов.
по одному из критериев: 1) СКО положения пункта относительно исходного, 2) СКО взаимного положения пунктов.
8. Строительная сетка - система координат, закрепленная на местности. Стороны строительной сетки направляются вдоль оси X и Y, т.е. вдоль поперечных и продольных осей основных сооружений.
Строительная сетка строится в следующем порядке:
1) приблизительно разбивается базовый прямоугольник 2х3 км. Левый угол принимается за начало координат. Стороны прямоугольника разбиваются с точностью 10 см на отрезки равной длины 200 м.
2) угловые точки закрепляются фундамент центрами и на их основе строится высокоточная триангуляционная сеть в виде четырехугольника. Сеть свободная. Условная исходная точка 8. Измеряется базис 8-9 и задается исходный дирекционный угол стороны 8-9. В результате уравнивания сети триангуляции получают координаты точек 0, 7, 8, 9 - первая ступень создания строительной сетки.
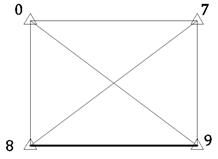
3) создают вторую ступень строительной сетки. Все промежуточные точки закрепляются железобетонными центрами и прокладываются полигонометрические хода. Измеряются β1, β2, β3,…, S1, S2, S3,… и т.д. Сеть полигонометрии является второй ступенью, опирающаяся на первую. Сеть полигонометрии уравнивается, и вычисляются координаты всех точек.
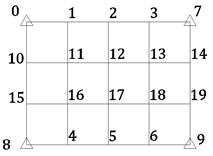
4)выполняется редуцирование точек. Редуцирование делается с целью создания правильных прямоугольников или квадратов внутри сетки. Редуцирование делается в следующем порядке. Пусть дирекционный угол линии 8-0 на первой ступени был задан
α8-0 - заданное
α8-0 = 0º00’00’’
Тогда координаты
x15=200,00 м
y15 = 0,00 м
Однако в результате уравнивания
x15=201,16 м
y15 = 0,57 м
Тогда на местности находится точка 15`. Необходимо 15`передвинуть в положение 15. Для этого вычисляется дирекционный угол α и расстояние S.
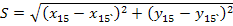
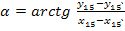
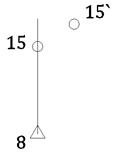
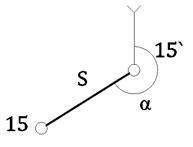
В точке 15` теодолитам откладывается угол α, а вдоль полученного направления сторону S. Фиксируется точка 15.
Контроль редуцирования: все углы 90º с точным выполнением измерений, а стороны должны быть равны номинальным длинам с точностью ±10 мм. Проектирование инженерных сооружений делается на основе строительной сетки, продольные и поперечные оси сооружений располагаются вдоль линий сетки.
Требования к точности расположения пунктов строительной сетки. Поскольку оси выносятся относительно точек сетки, то покажем зависимость точности положения оси.
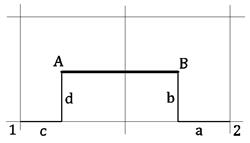
Для выноса точки В отложим расстояние а, угол 90º, расстояние b. Для выноса точки А - расстояние с, угол 90º, расстояние d. Контролем выноса оси АВ является соответствие длины АВ её проектному значению. Отличие в зависимости от строительных норм и правил может составлять от ±1 см до ±3 см.
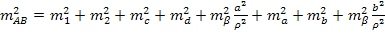
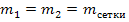
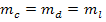
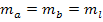
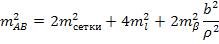
Исходя из функции, задав 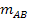 , можно рассчитать
, можно рассчитать 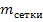 при заданной точности линейных измерений
при заданной точности линейных измерений 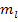 и угловых измерений
и угловых измерений 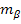 .
.
Дата добавления: 2016-10-26; просмотров: 3612;











