Вскрытие шифрования и подписи с использованием RSA
Имеет смысл подписывать сообщение перед шифрованием (см. раздел 2.7), но на практике никто не выполняет этого. Для RSA можно вскрыть протоколы, шифрующие сообщение до его подписания [48].
Àëèñà хочет послать сообщение Áîáу. Сначала она шифрует его открытым ключом Áîáа, а затем подписывает своим закрытым ключом. Ее зашифрованное и подписанное сообщение выглядит так:
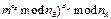
Вот как Áîá может доказать, что Àëèñà послала ему m', а не m. Так как Áîáу известно разложение на множители nB(это его собственный модуль), он может вычислить дискретные логарифмы по основанию nB. Следовательно, ему нужно только найти x, для которого
m'x = m mod nB
Тогда, если он может опубликовать xeBв качестве своего нового открытого показателя степени и сохранить свой прежний модуль nB, он сможет утверждать, что Àëèñà послала ему сообщение m', зашифрованное этим новым показателем.
В некоторых случаях это особенно неприятное вскрытие. Заметим, что хэш-функции не решают проблему. Однако она решается при использовании для каждого пользователя фиксированного показателя шифрования.
Стандарты
RSA de factoявляется стандартом почти по всему миру. ISO почти, but not quite, created an RSA digital-signature standard; RSA служит информационным дополнением ISO 9796 [762.]. Французское банковское сообщество приняло RSA в качестве стандарта [525], так же поступили и австралийцы [1498]. В Соединенных Штатах из-за давления NSA и патентных вопросов в настоящее время нет стандарта для шифрования с открытым ключом. Многие американские компании используют PKCS (см. раздел 24.14), написанный RSA Data Security, Inc. RSA определен и в качестве чернового банковского стандарта ANSI [61].
Патенты
Алгоритм RSA запатентован в Соединенных Штатах [1330], но ни водной другой стране. PKP получила лицензию вместе с другими патентами в области криптографии с открытыми ключами (раздел 25.5). Срок действия патента США истекает 20 сентября 2000 года.
Pohlig-Hellman
Схема шифрования Pohlig-Hellman [1253] похожа на RSA. Это не симметричный алгоритм, так как для шифрования и дешифрирования используются различные ключи. Это не схема с открытым ключом, потому что ключи легко получаются один из другого, и ключ шифрования, и ключ дешифрирования должны храниться в секрете. Как и в RSA,
C= Pemod n
P= Cdmod n
где
ed º 1 (mod какое-нибудь составное число)
В отличие от RSA nне определяется с помощью двух простых чисел и остается частью закрытого ключа. Если у кого-нибудь есть eи n, он может вычислить d. Íå çíàÿ eили d, противник будет вынужден вычислить
e = logpC mod n
Мы уже видели, что это является трудной проблемой.
Патенты
Алгоритм Pohlig-Hellman запатентован в США [722] и в Канаде. PKP получила лицензию вместе с другими патентами в области криптографии с открытыми ключами(см. раздел 25.5).
Rabin
Безопасность схемы Рабина (Rabin) [1283, 1601] опирается на сложность поиска квадратных корней по модулю составного числа. Эта проблема аналогична разложению на множители. Вот одна из реализаций этой схемы.
Сначала выбираются два простых числа pи q, конгруэнтных 3 mod 4. Эти простые числа являются закрытым ключом, а их произведение n =pq - открытым ключом.
Для шифрования сообщения M(M должно быть меньше n), просто вычисляется
C= M2mod n
Дешифрирование сообщения также несложно, но немного скучнее. Так как получатель знает pи q, он может решить две конгруэнтности с помощью китайской теоремы об остатках. Вычисляется
m1 = C(p+1)/4 mod p
m2= (p- C(p+1)/4) mod p
m3 = C(q+1)/4 mod q
m4= (q- C(q+1)/4) mod q
Затем выбирается целые числа a= q(q-1 mod p) и b= p(p-1 mod q). Четырьмя возможными решениями являются:
M1= (am1+ bm3) mod n
M2= (am1+ bm4) mod n
M3= (am2+ bm3) mod n
M4= (am2+ bm4) mod n
Один из четырех результатов, M1, M2, M3 и M4, равно M. Если сообщение написано по английски, выбрать правильное Mi нетрудно. С другой стороны, если сообщение является потоком случайных битов (скажем, для генерации ключей или цифровой подписи), способа определить, какое Mi - правильное, нет. Одним из способов решить эту проблему служит добавление к сообщению перед шифрованием известного заголовка.
Williams
Хью Вильямс (Hugh Williams) переопределил схему Рабина, чтобы устранить эти недостатки [1601]. В его схеме pи qвыбираются так, чтобы
pº 3 mod 8
q º 7 mod 8
и
N= pq
Кроме того, используется небольшое целое число, S, для которого J(S,N) = -1. (J - это символ Якоби - см. раздел I I .3). Nи S опубликовываются. Секретным ключом является k, для которого
k= 1/2 (1/4 (p - 1) (q - 1) + 1)
Для шифрования сообщения M вычисляется c1, такое что J(M,N) = 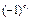 . Затем вычисляется M'= (
. Затем вычисляется M'= ( 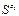 *M) mod N.Как и в схеме Рабина, C= M'2mod N. И c2 = M'mod 2. Окончательным шифротекстом сообщения является тройка:
*M) mod N.Как и в схеме Рабина, C= M'2mod N. И c2 = M'mod 2. Окончательным шифротекстом сообщения является тройка:
(C, cl, c2)
Для дешифрирования C, получатель вычисляет M"с помощью
Ckº± M"(mod N)
Правильный знак M"определяет c2. Наконец
M= ( 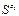 *
* 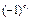 *M")mod N
*M")mod N
Впоследствии Вильямс улучшил эту схему в [1603, 1604, 1605]. Вместо возведения в квадрат открытого текста сообщения, возведите его в третью степени. Большие простые числа должны быть конгруэнтны 1 по модулю 3, иначе открытый и закрытый ключи окажутся одинаковыми. Даже лучше, существует только одна уникальная расшифровка каждого шифрования.
Преимущество схем Рабина и Вильямса перед RSA в том, что доказано, что они также безопасны, как и разложение на множители. Однако перед вскрытием с выбранным шифротекстом они совершенно беззащитны. Если вы собираетесь использовать эти схемы для случаев, когда взломщик может выполнить такое вскрытие (íàïðèìåð, алгоритм цифровой подписи, когда взломщик может выбирать подписываемые сообщения), не забывайте использовать перед подписанием однонаправленную хэш-функцию. Рабин предложил другой способ защититься от такого вскрытия: к каждому сообщению перед хэшированием и подписанием добавляется уникальная случайная строка. К несчастью, после добавления однонаправленной хэш-функцией тот факт, что система столь же безопасна, как и разложение на множители, больше не является доказанным [628]. Хотя с практической точки зрения добавление хэширования не может ослабить систему.
Другими вариантами схемы Рабина являются [972, 909, 696, 697, 1439, 989]. Двумерный вариант описан в [866, 889].
ElGamal
Схему EIGamal [518,519] можно использовать как для цифровых подписей, так и для шифрования, его безопасность основана на трудности вычисления дискретных логарифмов в конечном поле.
Для генерации пары ключей сначала выбирается простое число p и два случайных числа, gи x, оба эти числа должны быть меньше p. Затем вычисляется
y= gxmod p
Открытым ключом являются y, g и p. И g, и pможно сделать общими для группы пользователей. Закрытым ключом является x.
Подписи ElGamal
Чтобы подписать сообщение M, сначала выбирается случайное число k, взаимно простое с p-1. Затем вычисляется
a= gkmod p
и с помощью расширенного алгоритма Эвклида находится bв следующем уравнении:
M= (xa + kb) mod (p - 1)
Подписью является пара чисел: aи b. Случайное значение k должно храниться в секрете. Для проверки подписи нужно убедиться, что
yaabmod p= gM mod p
Каждая подпись или шифрование EIGamal требует нового значения k, и это значение должно быть выбрано случайным образом. Если когда-нибудь Ева раскроет k, используемое Àëèñой, она сможет раскрыть закрытый ключ Алисы x. Если Ева когда-нибудь сможет получить два сообщения, подписанные или зашифрованные с помощью одного и того же k, то она сможет раскрыть x, даже не зная значение k. Описание ElGamal сведено в Табл. 19-5.
Табл. 19-5.
Подписи ElGamal
Открытый ключ:
| p | простое число (может быть общим для группы пользователей) |
| g | <p (может быть общим для группы пользователей) |
| y | =gx mod p |
Закрытый ключ:
| x | <p |
Подпись:
| k | выбирается случайным образом, взаимно простое с p-1 |
| a | (подпись) =gk mod p |
| b | (подпись), такое что M= (xa + kb) mod (p - 1) |
Проверка:
| Подпись считается правильной, если yaabmod p= gM mod p |
Íàïðèìåð, выберем p= 11 и g= 2, а закрытый ключ x= 8. Вычислим
y= gx mod p= 28 mod 11 = 3
Открытым ключом являются y= 3, g= 2 и p= 11. Чтобы подписать M = 5, сначала выберем случайное число k=9. Убеждаемся, что gcd(9, 10)= 1. Вычисляем
a= gkmod p= 29 mod 11 = 6
и с помощью расширенного алгоритма Эвклида находим b:
M= (xa + kb) mod (p - 1)
5 = (8*6 + 9*b) mod 10
Решение: b= 3, а подпись представляет собой пару: a= 6 и b= 3.
Для проверки подписи убедимся, что
yaabmod p= gM mod p
3663 mod 11 = 25mod 11
Вариант EIGamal, используемый для подписей, описан в [1377]. Томас Бет (Thomas Beth) изобрел вариант схемы EIGamal, подходящий для доказательства идентичности [146]. Существуют варианты для проверки подлинности пароля [312] и для обмена ключами [773]. И еще тысячи и тысячи других (см. раздел 20.4).
Шифрование ElGamal
Модификация EIGamal позволяет шифровать сообщения. Для шифрования сообщения Mсначала выбирается случайное число k, взаимно простое с p- 1. Затем вычисляются
a= gkmod p
b= yk Mmod p
Пара (a,b) является шифротекстом. Обратите внимание, что шифротекст в два раза длиннее открытого текста. Для дешифрирования (a,b) вычисляется
M= b/axmod p
Так как axº gkx(mod p) и b/axº yk M/ax º gxk M/ gkx = M (mod p), то все работает (см. Табл. 19-6). По сути это то же самое, что и обмен ключами Диффи-Хеллмана (см. раздел 22.1)за исключением того, что y- это часть ключа, а при шифровании сообщение умножается на yk.
Табл. 19-6.
Шифрование ElGamal
Открытый ключ:
| p | простое число (может быть общим для группы пользователей) |
| g | <p (может быть общим для группы пользователей) |
| y | =gx mod p |
Закрытый ключ:
| x | <p |
Шифрование:
| k | выбирается случайным образом, взаимно простое с p-1 |
| a | (шифротекст) =gk mod p |
| b | (шифротекст)= yk Mmod p |
Дешифрирование:
| M (открытый текст) = b/axmod p |
Скорость
Некоторые примеры скорости работы программных реализаций EIGamal приведены в Табл. 19-7 [918].
Табл. 19-7.
Скорости EIGamal для различных длин модулей при 160-битовом показателе степени (на SPARC II)
| 512 битов | 768 битов | 1024 битов | |
| Шифрование | 0.33 с | 0.80 ñ | 1.09 ñ |
| Дешифрирование | 0.24 ñ | 0.58 ñ | 0.77 ñ |
| Подпись | 0.25 ñ | 0.47 ñ | 0.63 ñ |
| Проверка | l.37 ñ | 5.12 ñ | 9.30 c |
Патенты
ElGamal незапатентован. Но, прежде чем двигаться вперед и реализовывать алгоритм, нужно знать, что PKP считает, что этот алгоритм попадает под действие патента Диффи-Хеллмана [718]. Однако срок действия патента Диффи-Хеллмана заканчивается 29 апреля 1997 года, что делает ElGamal первым криптографическим плгоритмом с открытыми ключами, пригодным для шифрования и цифровых подписей и несвязанным в Соединенных Штатах патентами. Я не могу дождаться этого момента.
McEliece
В 1978 году Роберт МакЭлис (Robert McEliece) разработал криптосистему с открытыми ключами на основе теории алгебраического кодирования [1041]. Этот алгоритм использует существование определенного класса исправляющих ошибки кодов, называемых кодами Гоппа (Goppa).Он предлагал создать код Гоппа и замаскировать его как обычный линейный код. Существует быстрый алгоритм декодирования кодов Гоппа, но общая проблема найти слово кода по данному весу в линейном двоичном коде является NP-полной. Хорошее описание этого алгоритма можно найти в [1233], см. также [1562]. Ниже приведен только краткий обзор.
Пусть dH(x,y) обозначает расстояние Хэмминга между xи y. Числа n, k и tслужат параметрами системы.
Закрытый ключ состоит из трех частей: G'- это матрица генерации года Гоппа, исправляющего tошибок. P-это матрица перестановок размером n*n. S- это nonsingular матрица размером k*k.
Открытым ключом служит матрица G размером k*n: G= SG'P.
Открытый текст сообщений представляет собой строку kбитов в виде k-элементного вектора над полем GF(2).
Для шифрования сообщения случайным образом выбирается n-элементный вектор z над полем GF(2), для которого расстояние Хэмминга меньше или равно t.
c = mG+ z
Для дешифрирования сообщения сначала вычисляется c'= cP-1. Затем с помощью декодирующего алгоритма для кодов Гоппа находится m', для которого dH(m'G,c) меньше или равно t.Наконец вычисляется m = m'S-1.
В своей оригинальной работе МакЭлис предложил значения n= 1024, t= 50 и k= 524. Это минимальные значения, требуемые для безопасности.
Хотя этот алгоритм был одним из первых алгоритмов с открытыми ключами, и вне появлялось публикаций о его успешном криптоаналитическом вскрытии, он не получил широкого признания в криптографическом сообществе. Схема на два-три порядка быстрее, чем RSA, но у нее есть ряд недостатков. Открытый ключ огромен: 219 битов. Сильно увеличивается объем данных - шифротекст в два раза длиннее открытого текста.
Ряд попыток криптоанализа этой системы можно найти в [8, 943, 1559, 306]. Ни одна из них не достигла успеха для общего случая, хотя сходство между алгоритмом МакЭлиса и алгоритмом рюкзака немного волнует.
В 1991 два русских криптографа заявили, что взломали систему МакЭлиса с некоторыми параметрами [882]. В их статье это утверждение не было обосновано, и большинство криптографов не приняли во внимание этот результат. Еще одно выполненное русскими вскрытие, которое нельзя непосредственно использовать против системы МакЭлиса, описано в [1447, 1448]. Расширения McEliece можно найти в [424, 1227, 976].
Дата добавления: 2021-01-26; просмотров: 658;











