Криптоанализ Snefru

<85 86 878889 90 91 >

Используя дифференциальный криптоанализ, Бихам и Шамир показали небезопасность двухпроходного Snefru (с 128-битовым хэш-значением) [172]. Их способ вскрытия за несколько минут обнаруживает пару сообщений с одинаковым хэш-значением.

Для 128-битового Snefru их вскрытия работают лучше, чем вскрытие грубой силой для четырех и менее проходов. Вскрытие Snefru методом дня рождения требует 2⁶⁴ операций; дифференциальный криптоанализ может найти пару сообщений с одинаковым хэш-значением за 2^28.5операций для трехпроходного Snefru и за 2^44.5операций для четырехпроходного Snefru. Нахождение сообщения, хэш-значение которого совпадает с заданным, при использовании грубой силы требует 2¹²⁸ операций, при дифференциальном криптоанализе для этого нужно 2⁵⁶ операций для трехпроходного и 2⁸⁸операций для четырехпроходного Snefru.

Хотя Бихам и Шамир не анализировали 256-битовые хэш-значения, они провели анализ вплоть до 224-битовых хэш-значений. В сравнении с вскрытием методом дня рождения, требующим 2¹¹² операций они могут найти сообщения с одинаковым хэш-значением за 2^12.5 операций для двухпроходного Snefru, за 2³³ операций для трехпроходного Snefru и за для 2⁸¹операций для четырехпроходного Snefru.

В настоящее время Меркл рекомендует использовать Snefru по крайней мере с восемью проходами [1073]. Однако с таким количеством проходов алгоритм становится намного медленнее, чем MD5 или SHA.

N-хэш

N-хэш - это алгоритм, придуманный в 1990 году исследователями Nippon Telephone and Telegraph, теми же людьми, которые изобрели FEAL [1105, 1106]. N-хэш использует 128-битовые блоки сообщения, сложную рандомизирующую функцию, похожую на FEAL, и выдает 128-битовое хэш-значение.

Хэш-значениекаждого 128-битового блока является функцией блока и хэш-значения предыдущего блока.

H₀= I, где I- случайное начальное значение

H_i= g(M_i, H_i_-1) Å M_iÅ H_i_-1

Хэш-значение всего сообщения представляет собой хэш-значение последнего блока сообщения. Случайное начальное значение Iможет быть любым числом, определенным пользователем (даже одними нулями).

Функция g достаточно сложна. Схема алгоритма приведена на Рис. 18-2. Сначала переставляются левая и правая 64-битовые половины 128-битового хэш-значения предыдущего блока H_i_-1, а затем выполняется XOR с повторяющимся шаблоном (128-битовым) и XOR с текущим блоком сообщения M_i. Далее это значение каскадно преобразуется в N(на рисунках N= 8) стадий обработки. Другим входом стадии обработки является предыдущее хэш-значение, подвергнутое XOR с одной из восьми двоичных констант.

Рис. 18-2. Схема N-хэш.

Одна стадия обработки показана на Рис. 18-3. Блок сообщения разбивается на четыре 32-битовых значения. Предыдущее хэш-значение также разбивается на четыре 32-битовых значения. Функция f представлена на Рис. 18-4. Функции S₀ и S₁ те же самые, что и в FEAL.

S₀(a,b) = циклический сдвиг влево на два бита ((a + b) mod 256)

S₁(a,b) = циклический сдвиг влево на два бита((a + b + 1) mod 256)

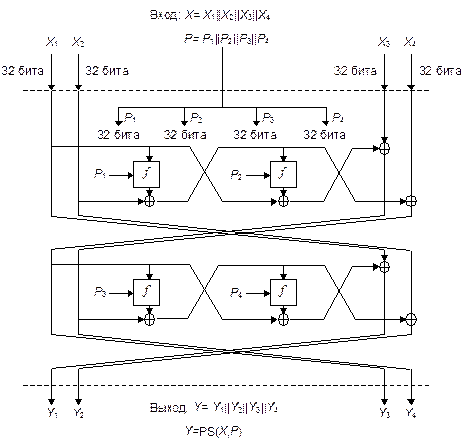
Рис. 18-3. Одна стадия обработки N-хэш.

Выход одной стадии обработки становится входом следующей стадии обработки. После последней стадии обработки выполняется XOR выхода с M_iи H_i_-₁, а затем к хэшированию готов следующий блок.

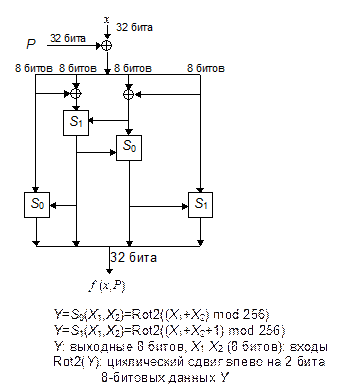
Рис. 18-4. Функция f.

Криптоанализ N-хэш

Берт ден Боер (Bert den Boer) открыл способ создавать столкновения в функции этапа N-хэш [1262]. Бихам и Шамир применили дифференциальный криптоанализ для вскрытия 6-этапной N-хэш [169, 172]. Конкретное выполненное ими вскрытие (конечно же, могли быть и другие) работает для любого N, делящегося на 3, и эффективнее вскрытия методом дня рождения для любого N, меньшего 15.

То же самое вскрытие может обнаруживать пары сообщений с одинаковым хэш-значением для 12-этапной N-хэш за 2⁵⁶ операций (для вскрытия грубой силой нужно 2⁶⁴ операций). N-хэш с 15 этапами безопасна по отношению к дифференциальному криптоанализу: для вскрытия потребуется 2⁷² операций.

Разработчики алгоритма рекомендуют использовать N-хэш не меньше, чем с 8 этапами [1106]. С учетом доказанной небезопасности N-хэш и FEAL (и ее скорости при 8 этапах) я рекомендую полностью отказаться от этого алгоритма.

MD4

MD4 - это однонаправленная хэш-функция, изобретенная Роном Ривестом [1318, 1319, 1321]. MD обозначает Message Digest (краткое изложение сообщения), алгоритм для входного сообщения выдает 128-битовое хэш-значение, или краткое изложение сообщения.

В [1319] Ривест описал цели, преследуемые им при разработке алгоритма:

Безопасность. Вычислительно невозможно найти два сообщения с одинаковым хэш-значением. Вскрытие грубой силой является самым эффективным.

Прямая безопасность. Безопасность MD4 не основывается на каких-либо допущениях, например, предположении о трудности разложения на множители.

Скорость. MD4 подходит для высокоскоростных программных реализаций. Она основана на простом наборе битовых манипуляций с 32-битовыми операндами.

Простота и компактность. MD4 проста, насколько это возможна, и не содержит больших структур данных или сложных программных модулей.

Удачна архитектура. MD4 оптимизирована для микропроцессорной архитектуры (особенно для микропроцессоров Intel), для более крупных и быстрых компьютеров можно выполнить любые необходимые изменения.

После первого появления алгоритма Берт ден Боер и Антон Босселаерс (Antoon Bosselaers) достигли успеха при криптоанализе последних двух из трех этапов алгоритма [202]. Ральфу Мерклу совершенно независимо удалось вскрыть первые два этапа [202]. Эли Бихам рассмотрел использование дифференциального криптоанализа против первых двух этапов MD4 [159]. Хотя все эти вскрытия не были распространены на полный алгоритм, Ривест усилил свою разработку. В результате появилась MD5.

MD5

MD5 - это улучшенная версия MD4 [1386, 1322]. Хотя она сложнее MD4, их схемы похожи, и результатом MD5 также является 128-битовое хэш-значение.

Описание MD5

После некоторой первоначальной обработки MD5 обрабатывает входной текст 512-битовыми блоками, разбитыми на 16 32-битовых подблоков. Выходом алгоритма является набор из четырех 32-битовых блоков, которые объединяются в единое 128-битовое хэш-значение.

Во первых, сообщение дополняется так, чтобы его длина была на 64 бита короче числа, кратного 512. Этим дополнением является 1, за которой вплоть до конца сообщения следует столько нулей, сколько нужно. Затем, к результату добавляется 64-битовое представление длины сообщения (истинной, до дополнения). Эти два действия служат для того, чтобы длина сообщения была кратна 512 битам (что требуется для оставшейся части алгоритма), и чтобы гарантировать, что разные сообщения не будут выглядеть одинаково после дополнения. Инициализируются четыре переменных:

A = 0x01234567

B = 0x89abcdef

C= 0xfedcba98

D= 0x76543210

Они называются переменными сцепления.

Теперь перейдем к основному циклу алгоритма. Этот цикл продолжается, пока не исчерпаются 512-битовые блоки сообщения.

Четыре переменных копируются в другие переменные: Aв a, B в b, C в c и D в d.

Главный цикл состоит из четырех очень похожих этапов (у MD4 было только три этапа). На каждом этапе 16 раз используются различные операции. Каждая операция представляет собой нелинейную функцию над тремя из a, b, c и d. Затем она добавляет этот результат к четвертой переменной, подблоку текста и константе. Далее результат циклически сдвигается вправо на переменное число битов и добавляет результат к одной из переменных a, b, c и d. Наконец результат заменяет одну из переменных a, b, c и d. См. Рис. 18-5 и Рис. 18-6. Существуют четыре нелинейных функции, используемые по одной в каждой операции (для каждого этапа - другая функция).

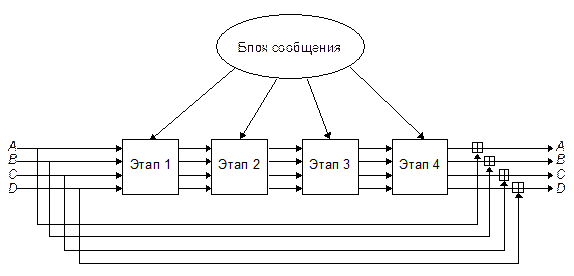
Рис. 18-5. Главный цикл MD5.

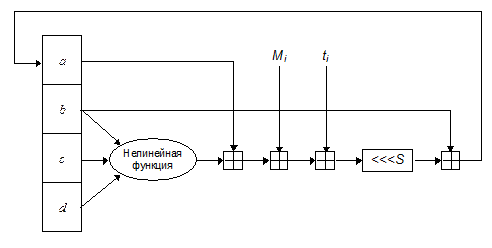
Рис. 18-6. Одна операция MD5.

F(X,Y,Z) = (X Ù Y) Ú ((ØX) Ù Z)

G(X,Y,Z) = (X Ù Z) Ú (Y Ù (ØZ))

H(X,Y,Z) = XÅ Y Å Z

I(X,Y,Z) = Y Å(X Ú (ØZ))

(Å - это XOR, Ù - AND, Ú - OR, а Ø - NOT.)

Эти функции спроектированы так, чтобы, если соответствующие биты X, Y и Z независимы и несмещены, каждый бит результата также был бы независимым и несмещенным. Функция F - это побитовое условие: если X, то Y, иначе Z. Функция H - побитовая операция четности.

Если M_j обозначает j-ый подблок сообщения (от 0 до 15), а <<<s обозначает циклический сдвиг влево на s битов, то используются следующие четыре операции:

FF(a,b,c,d,M_j,s,t_i) означает a= b+ ((a + F(b,c,d) + M_j + t_i) <<<s)

GG(a,b,c,d,M_j,s,t_i) означает a= b+ ((a + G(b,c,d) + M_j + t_i) <<<s)

HH(a,b,c,d,M_j,s,t_i) означает a= b+ ((a + H(b,c,d) + M_j + t_i) <<<s)

II(a,b,c,d,M_j,s,t_i) означает a= b+ ((a + I(b,c,d) + M_j + t_i) <<<s)

Четыре этапа (64 действия выглядят следующим образом):

Этап 1:

FF(a, b, c, d, M₀, 7, 0xd76aa478)

FF(d, a, b, c, M₁, 12, 0xe8c7b756)

FF(c, d, a, b, M₂, 17, 0x242070db)

FF(b, c, d, a, M₃, 22, 0xc1bdceee)

FF(a, b, c, d, M₄, 7, 0xf57c0faf)

FF(d, a, b, c, M₅, 12, 0x4787c62a)

FF(c, d, a, b, M₆, 17, 0xa8304613)

FF(b, c, d, a, M₇, 22, 0xfd469501)

FF(a, b, c, d, M₈, 7, 0x698098d8)

FF(d, a, b, c, M₉, 12, 0x8b44f7af)

FF(c, d, a, b, M₁₀, 17, 0xffff5bb1)

FF(b, c, d, a, M₁₁, 22, 0x895cd7be)

FF(a, b, c, d, M₁₂, 7, 0x6b901122)

FF(d, a, b, c, M₁₃, 12, 0xfd987193)

FF(c, d, a, b, M₁₄, 17, 0xa679438e)

FF(b, c, d, a, M₁₅, 22, 0x49b40821)

Этап 2:

GG(a, b, c, d, M₁, 5, 0xf61e2562)

GG(d, a, b, c, M₆,9, 0xc040b340)

GG(c, d, a, b, M₁₁, 14, 0x265e5a51)

GG(b, c, d, a, M₀, 20, 0xe9b6c7aa)

GG(a, b, c, d, M₅, 5, 0xd62fl05d)

GG(d, a, b, c, M₁₀,9, 0x02441453)

GG(c, d, a, b, M₁₅, 14, 0xd8ale681)

GG(b, c, d, a, M₄, 20, 0xe7d3fbc8)

GG(a, b, c, d, M₉, 5, 0x2,lelcde6)

GG(d, a, b, c, M₁₄,9, 0xc33707d6)

GG(c, d, a, b, M₃, 14, 0xf4d50d87)

GG(b, c, d, a, M₈, 20, 0x455al4ed)

GG(a, b, c, d, M₁₃, 5, 0xa9e3e905)

GG(d, a, b, c, M₂,9, 0xfcefa3f8)

GG(c, d, a, b, M₇, 14, 0x676f02d9)

GG(b, c, d, a, M₁₂, 20, 0x8d2a4c8a)

Этап 3:

HH(a, b, c, d, M₅, 4, 0xfffa3942)

HH(d, a, b, c, M₈, 11, 0x8771f681)

HH(c, d, a, b, M₁₁, 16, 0x6d9d6122)

HH(b, c, d, a, M₁₄, 23, 0xfde5380c)

HH(a, b, c, d, M₁, 4, 0xa4beea44)

HH(d, a, b, c, M₄, 11, 0x4bdecfa9)

HH(c, d, a, b, M₇, 16, 0xf6bb4b60)

HH(b, c, d, a, M₁₀, 23, 0xbebfbc70)

HH(a, b, c, d, M₁₃, 4, 0x289b7ec6)

HH(d, a, b, c, M₀, 11, 0xeaa127fa)

HH(c, d, a, b, M₃, 16, 0xd4ef3085)

HH(b, c, d, a, M₆, 23, 0x04881d05)

HH(a, b, c, d, M₉, 4, 0xd9d4d039)

HH(d, a, b, c, M₁₂, 11, 0xe6db99e5)

HH(c, d, a, b, M₁₅, 16, 0x1fa27cf8)

HH(b, c, d, a, M₂, 23, 0xc4ac5665)

Этап 4:

II(a, b, c, d, M₀, 6, 0xf4292244)

II(d, a, b, c, M₇, 10, 0x432aff97)

II(c, d, a, b, M₁₄, 15, 0xab9423a7)

II(b, c, d, a, M₅, 21, 0xfc93a039)

II(a, b, c, d, M₁₂, 6, 0x655b59c3)

II(d, a, b, c, M₃, 10, 0x8f0ccc92)

II(c, d, a, b, M₁₀, 15, 0xffeff47d)

II(b, c, d, a, M₁, 21, 0x85845ddl)

II(a, b, c, d, M₈,6, 0x6fa87e4f)

II(d, a, b, c, M₁₅, 10, 0xfe2ce6e0)

II(c, d, a, b, M₆,15, 0xa3014314)

II(b, c, d, a, M₁₃, 21, 0x4e081lal)

II(a, b, c, d, M₄, 6, 0xf7537e82)

II(d, a, b, c, M₁₁, 10, 0xbd3af235)

II(c, d, a, b, M₂, 15, 0x2ad7d2bb)

II(b, c, d, a, M₉, 21, 0xeb86d391)

Эти константы, t_i, выбирались следующим образом:

На i-ом этапе t_iявляется целой частью 2³²*abs(sin(i)), где i измеряется в радианах.

После всего этого a, b, c и d добавляются к A, B, C и D, соответственно, и алгоритм продолжается для следующего блока данных. Окончательным результатом служит объединение A, B, C и D.

БезопасностьMD5

Рон Ривест привел следующие улучшения MD5 в сравнении с MD4 [1322]:

1. Добавился четвертый этап.

2. Теперь в каждом действии используется уникальная прибавляемая константа.

3. Функция G на этапе 2 с ((XÙY)Ú(XÙZ)Ú(YÙZ)) была изменена на (XÙZ)Ú(YÙ(ØZ)), чтобы сделать G менее симметричной.

4. Теперь каждое действие добавляется к результату предыдущего этапа. Это обеспечивает более быстрый лавинный эффект.

5. Изменился порядок, в котором использовались подблоки сообщения на этапах 2 и 3, чтобы сделать шаблоны менее похожими.

6. Значения циклического сдвига влево на каждом этапе были приближенно оптимизированы для ускорения лавинного эффекта. Четыре сдвига, используемые на каждом этапе, отличаются от значений, используемых на других этапах.

Том Берсон (Tom Berson) попытался применить дифференциальный криптоанализ к одному этапу MD5 [144], но его вскрытие не оказалось эффективным ни для одного из четырех этапов. Более успешное вскрытие ден Боера и Босселаерса, использующее функцию сжатия, привело к обнаружению столкновений в MD5 [203, 1331, 1336]. Само по себе это вскрытие невозможно для вскрытия MD5 в практических приложениях, оно не влияет и на использование MD5 в алгоритмах шифрования, подобных Luby-Rackoff (см. раздел 14.11). Успех этого вскрытия означает только, что одна из основных целей проектирования MD5- создать устойчивую к столкновениям функцию сжатия - не была достигнута. Хотя справедливо, что "кажется, что у функции сжатия есть слабое место, но это практически не влияет на безопасность хэш-функции " [1336], я отношусь к использованию MD5 очень осторожно.

MD2

MD2 - это другая 128-битовая однонаправленная хэш-функция, разработанная Роном Ривестом [801, 1335]. Она, вместе с MD5, используется в протоколах PEM (см. раздел 24.10). Безопасность MD2 опирается на случайную перестановку байтов. Эта перестановка фиксирована и зависит от разрядов p. S₀, S₁, S₂, . . . , S₂₅₅ и являются перестановкой. Чтобы выполнить хэширование сообщения M:

(1) Дополните сообщение iбайтами, значение i должно быть таким, чтобы длина полученного сообщения была кратна 16 байтам.

(2) Добавьте к сообщению 16 байтов контрольной суммы.

(3) Проинициализируйте 48-байтовый блок: X₀, X₁, X₂, . . ., X₄₇. Заполните первые 16 байтов X нулями, во вторые 16 байтов X скопируйте первые 16 байтов сообщения, а третьи 16 байтов X должны быть равны XOR первых и вторых 16 байтов X.

(4) Вот как выглядит функция сжатия:

t= 0

For j= 0 to 17

For k= 0 to 47

t= X_tXORS_t

X_k= t

t= (t + j) mod 256

(5) Скопируйте во вторые 16 байтов Xвторые 16 байтов сообщения, а третьи 16 байтов X должны быть равны XOR первых и вторых 16 байтов X. Выполните этап (4). Повторяйте этапы (5) и (4) по очереди для каждых 16 байтов сообщения.

(6) Выходом являются первые 16 байтов X.

Хотя в MD2 пока не было найдено слабых мест (см. [1262]), она работает медленнее большинства других предлагаемых хэш-функций.

<85 86 878889 90 91 >

Дата добавления: 2021-01-26; просмотров: 283;

Поиск по сайту

Узнать еще