Криптоанализ LOKI91
Кнудсен предпринял попытку криптоанализа LOKI91 [854, 858], но нашел, что этот алгоритм устойчив к дифференциальному криптоанализу. Однако ему удалось обнаружить, что вскрытие со связанными ключами для выбранных открытых текстов уменьшает сложность вскрытия грубой силой почти вчетверо. Это вскрытие использует слабость использования ключа и может быть также применено, если алгоритм используется в качестве однонаправленной хэш-функции (см. раздел 18.11).
Другое вскрытие со связанными ключами может вскрыть LOKI91 с помощью 232 выбранных открытых текстов для выбранных ключей или с помощью 248 известных открытых текстов для выбранных ключей [158]. Это вскрытие не зависит от числа этапов алгоритма. (В той же работе Бихам вскрывает LOKI89, используя криптоанализ со связанными ключами, с помощью 217 выбранных открытых текстов для выбранных ключей или с помощью 233 известных открытых текстов для выбранных ключей.) Несложно повысить устойчивость LOKI91 к вскрытию такого типа, усложнив схему использования ключа.
Патенты и лицензии
LOKI не запатентован. Кто угодно может реализовать алгоритм и использовать его. Исходный код, приведенный в этой книге, написан в Университете Нового Южного Уэльса. При желании использовать эту реализацию (или другие реализации, которые на несколько порядков быстрее) в коммерческом продукте обращайтесь к Директору CITRAD, Факультет компьютерных наук, Университетский колледж, Университет Нового Южного Уэльса, Академия австралийских вооруженных сил, Канберра, Австралия (Director CITRAD, Department of Computer Science, University College, UNSW, Australian Defense Force Academy, Canberra ACT 2600, Australia; FAX: +61 6 268 8581.
KHUFU и KHAFRE
В 1990 году Ральф Меркл (Ralph Merkle) предложил два алгоритма. В основе их проектирования лежали следующие принципы [1071]:
1. 56-битовый размер ключа DES слишком мал. Так как стоимость увеличения размера ключа пренебрежимо мала (компьютерная память недорога и доступна), он должен быть увеличен.
2. Интенсивное использование перестановок в DES хотя и удобно для аппаратных реализаций, чрезвычайно затрудняет программные реализации. Наиболее быстрые реализации DES выполняют перестановки табличным образом. Просмотр таблицы может обеспечить те же характеристики "рассеяния", что и собственно перестановки, и может сделать реализацию намного более гибкой.
3. S-блоки DES, всего с 64 4-битовыми элементами, слишком малы. Теперь с увеличением памяти должны увеличиться и S-блоки. Более того, все восемь S-блоков используются одновременно. Хотя это и удобно для аппаратуры, для программной реализации это кажется ненужным ограничением. Должны быть реализованы больший размер S-блоков и последовательное (а не параллельное) их использование.
4. Широко признано, что начальная и заключительная перестановки криптографически бессмысленны, поэтому они должны быть устранены.
5. Все быстрые реализации DES заранее рассчитывают ключи для каждого этапа. При данном условии нет смысла усложнять эти вычисления.
6. В отличие от DES критерии проектирования S-блоков должны быть общедоступны.
К этому перечню Меркл, возможно, теперь добавил бы "устойчивость к дифференциальному и линейному криптоанализу", ведь в то время эти способы вскрытия не были известны.
Khufu
Khufu - это 64-битовый блочный шифр. 64-битовый открытый тест сначала разбивается на две 32-битовые половины, L и R. Над обеими половинами и определенными частями ключа выполняется операция XOR. Затем, аналогично DES, результаты проходят через некоторую последовательность этапов. На каждом этапе младший значащий байт L используется в качестве входных данных S-блока. У каждого S-блока 8 входных битов и 32 выходных бита. Далее выбранный в S-блоке 32-битовый элемент подвергается операции XOR с R. Затем L циклически сдвигается не несколько из восьми битов, L и R меняются местами, и этап заканчивается. Сам S-блок не является статическим, но меняется каждые восемь этапов. Наконец после последнего этапа над L и R выполняется операция XOR с другими частями ключа, и половины объединяются, образуя блок шифротекста.
Хотя части ключа используются для XOR с блоком шифрования в начале и в конце алгоритма, главная цель ключа -генерация S-блоков. Эти S-блоки - секретны, по сути являются они являются частью ключа. Полный размер ключа Khufu равен 512 битам (64 байтам), алгоритм предоставляет способ генерации S-блоков по ключу. Количество этапов алгоритма остается открытым. Меркл упомянул, что 8-этапный Khufu чувствителен к вскрытию с выбранным открытым текстом и рекомендует 16, 24 или 32 этапа [1071]. (Он ограничивает выбор количества этапов числами, кратными восьми.)
Так как в Khufu используются зависимые от ключа и секретные S-блоки, он устойчив к дифференциальному криптоанализу. Существует дифференциальное вскрытие 16-этапного Khufu, которое раскрывает ключ после 231 выбранных открытых текстов [611], но его не удалось расширить на большее количество этапов. Если лучшим способом вскрыть Khufu является грубая сила, то его надежность производит сильное впечатление. 512-битовый ключ обеспечивает сложность 2512 - огромное число при любых условиях.
Khafre
Khafre - это вторая из криптосистем, предложенных Мерклом [1071]. (Khufu (Хуфу) и Khafre (Хафр) - это имена египетских фараонов.) По конструкции этот алгоритм похож на Khufu, но он спроектирован для приложений, не использующих предварительных вычислений. S-блоки не зависят от ключа. Вместо этого Khafre использует фиксированные S-блоки. Блок шифрования подвергается операции XOR с ключом не только перед первым этапом и после последнего, но и после каждых 8 этапов шифрования.
Меркл предположил, что с Khafre должны использоваться 64- или 128-битовые ключи, и что для Khafre потребуется больше этапов, чем для Khufu. Это наряду с тем, что каждый этап Khafre сложнее этапа Khufu, делает Khafre более медленным. Зато для Khafre не нужны никакие предварительны расчеты, что позволяет быстрее шифровать небольшие порции данных.
В 1990 году Бихам и Шамир применили свой метод дифференциального анализа против Khafre [170]. Им удалось взломать 16-этапный Khafre с помощью вскрытия с выбранным открытым текстом после 1500 различных шифрований. На их персональном компьютере это заняло около часа. Преобразование этого вскрытия во вскрытие с известным открытым текстом потребует около 238 шифрований. Khafre с 24 этапами может быть вскрыт с помощью вскрытия с выбранным открытым текстом за 253 шифрования, а с помощью вскрытия с известным открытым текстом - за 259 шифрования.
Патенты
И Khufu, и Khafre запатентованы [1072]. Исходный код этих алгоритмов содержится в патенте. При желании получить лицензию на любой или оба алгоритма следует обратиться к директору по лицензированию корпорации Xerox (Director of Licensing, Xerox Corporation, P.0. Box 1600, Stamford, CT, 06904-1600).
RC2
RC2 представляет собой алгоритм с переменной длиной ключа, спроектированный Роном Ривестом (Ron Rivest) для RSA Data Security, Inc. (RSADSI). Очевидно "RC" - это сокращенное "Ron's Code'' ("Код Рона"), хотя официально это "Rivest Cipher'' ("Шифр Ривеста"). (RC3 был взломан в RSADSI в процессе разработки, RC1 не вышел за пределы записной книжки Ривеста.) Он представляет собой частную собственность, и его детали не были опубликованы. Не думайте ни минуты, что это увеличивает его безопасность. RC2 уже появился в коммерческих продуктах. Насколько мне известно, RC2 не был запатентован и защищен только как торговый секрет.
RC2 - это шифр с 64-битовым блоком и переменной длиной ключа, предназначенный заменить DES. В соответствии с утверждениями компании программные реализации RC2 в три раза быстрее DES. Алгоритм может использовать ключ переменной длины, от 0 байтов до максимальной длины строки, поддерживаемой компьютерной системой, скорость шифрования не зависит от размера ключа. Этот ключ предварительно используется для заполнения 128-байтовой таблицы, зависящей от ключа. Поэтому множество действительно различных ключей составляет 21024. RC2 не использует S-блоков [805], используются две операции - "смешивание" и "перемешивание" ("mix" и "mash"), для каждого этапа выбирается одна из них. В соответствии с литературой [1334]:
. . . RC2 не является итеративным блочным шифром. Это предполагает, что RC2 более устойчив к дифференциальному и линейному криптоанализу, чем другие блочные шифры, безопасность которых опирается на копирование схемы DES.
Отказ RSADSI опубликовать RC2 заставляет сомневаться в намерениях этой компании. Она обещает предоставить детали алгоритма всем, кто подпишет соглашение о нераспространении информации, и утверждает, что позволит криптоаналитикам опубликовать любые обнаруженные негативные результаты. Мне неизвестно ни об одном криптоаналитике, не работающем в этой компании, кто бы исследовал алгоритм, так как это по сути означало бы выполнить работу по анализу для компании.
Тем не менее, Рон Ривест - не шарлатан. Он уважаемый и компетентный криптограф. Я лично в значительной степени верю в этот алгоритм, хотя я лично и не видел кода. RC4, также являющийся интеллектуальной собственностью RSADSI, был опубликован в Internet (см. раздел 17.1), и, вероятно, опубликование RC2 является только вопросом времени.
По соглашению между Ассоциацией издателей программного обеспечения (Software Publishers Association, SPA) и правительством США RC2 и RC4 (см. раздел 17.1) получили специальный экспортный статус (см. раздел 25.14). Процесс получения разрешения на экспорт продуктов, реализующих один из этих двух алгоритмов, значительно упрощен при условии, что длина ключа не превышает 40 битов.
Достаточен ли 40-битовый ключ? Существует всего один триллион возможных ключей. При условии, что наиболее эффективным методом криптоанализа является вскрытие грубой силой (большое допущение, ведь алгоритм никогда не был опубликован), и что микросхема грубого вскрытия может проверить миллион ключей в секунду, поиск правильного ключа займет 12.7 дней. Тысяча машин, работающих параллельно, смогут раскрыть ключ за двадцать минут.
RSA Data Security, Inc., утверждает, что, хотя шифрование и дешифрирования выполняются для быстро, исчерпывающего поиска потребуется намного больше времени. Заметное количество времени тратится на формирование плана использования ключа. Хотя это время пренебрежимо мало при шифровании и дешифрировании сообщений, это не так при проверке каждого возможного ключа.
Правительство США никогда не позволило бы экспортировать любой алгоритм, который оно, по крайней мере в теории, не смогло бы вскрыть. Оно может создать магнитную ленту или CD с конкретным блоком открытого текста, зашифрованным каждым возможным ключом. Для вскрытия сообщения остается только вставить ленту и сравнить блоки шифротекста в сообщении с блоками шифротекста на ленте. При совпадении можно проверить возможный ключ и посмотреть, имеет ли сообщение какой-нибудь смысл. Если они выберут часто встречающийся блок (все нули, ASCII-символы пробела, и т.д.), этот метод будет работать. Объем данных, нужный для хранения результатов шифрования 64-битового блока открытого текста всеми 1012 возможными ключами, составляет 8 терабайтов - вполне реально. По поводу лицензирования RC2 обращайтесь в RSADSI (см. раздел 25.4).
IDEA
Первый вариант шифра IDEA, предложенный Ксуеджа Лай (Xuejia Lai) и Джеймсом Масси (James Massey), появился в 1990 году [929]. Он назывался PES (Proposed Encryption Standard, предложенный стандарт шифрования). В следующем году, после демонстрации Бихамом и Шамиром возможностей дифференциального криптоанализа, авторы усилили свой шифр против такого вскрытия и назвали новый алгоритм IPES (Improved Proposed Encryption Standard, улучшенный предложенный стандарт шифрования) [931, 924]. В 1992 году название IPES было изменено на IDEA (International Data Encryption Algorithm, международный алгоритм шифрования данных) [925].
IDEA основывается на некоторых впечатляющих теоретических положениях и, хотя криптоанализ добился некоторых успехов в отношении вариантов с уменьшенным количеством этапов, алгоритм все еще кажется сильным. По моему мнению это самый лучший и самый безопасный блочный алгоритм, опубликованный сегодня.
Будущее IDEA пока неясно. Попыток заменить им DES предпринято не было, частично потому, что он запатентован и должен быть лицензирован для коммерческих приложений, и частично потому, что люди пока все еще ждут, наблюдая насколько хорошо поведет себя алгоритм в предстоящие годы криптоанализа. Его сегодняшняя известность объясняется тем, что он является частью PGP (см. раздел 24.12).
Обзор IDEA
IDEA является блочным шифром, он работает с 64-битовыми блоками открытого текста. Длина ключа - 128 битов. Для шифрования и дешифрирования используется один и тот же алгоритм.
Как и другие, уже рассмотренные блочные шифры IDEA использует и запутывание, и рассеяние. Флософия, лежащая в основе проекта, представляет собой "объединение операций из различных алгебраических групп". Смешиваются три алгебраические группы, и все они могут быть легко реализованы как аппаратно, так и программно:
— XOR
— Сложение по модулю 216
— Умножение по модулю 216 + 1. (Это операцию можно рассматривать как S-блок IDEA.)
Все эти операции (а в алгоритме используются только они, перестановки на битовом уровне не применяются) работают с 16-битовыми подблоками. Этот алгоритм даже эффективнее на 16-битовых процессорах.
Описание IDEA
Схема IDEA представлена на Рис. 13-9. 64-битовый блок данных делится на четыре 16-битовых подблока: X1, X2, X3 и X4. Эти четыре подблока становятся входными данными для первого этапа алгоритма. Всего в алгоритме восемь этапов. На каждом этапе четыре подблока подвергаются операциям XOR, сложениям и умножениям друг с другом и с шестью 16-битовыми подключами. Между этапами обмениваются местами второй и третий подблоки. Наконец четыре подблока объединяются с четырьмя подключами в окончательном преобразовании. На каждом этапе события происходят в следующей последовательности:
(1) Перемножаются X1 и первый подключ.
(2) Складываются X2 и второй подключ.
(3) Складываются X3 и третий подключ.
(4) Перемножаются X4 и четвертый подключ.
(5) Выполняется XOR над результатами этапов (1) и (3).
(6) Выполняется XOR над результатами этапов (2) и (4).
(7) Перемножаются результаты этапа (5) и пятый подключ.
(8) Складываются результаты этапов (6) и (7).
(9) Перемножаются результаты этапа (8) и шестой подключ.
(10) Складываются результаты этапов (7) и (9).
(11) Выполняется XOR над результатами этапов (1) и (9).
(12) Выполняется XOR над результатами этапов (3) и (9).
(13) Выполняется XOR над результатами этапов (1) и (10).
(14) Выполняется XOR над результатами этапов (4) и (10).
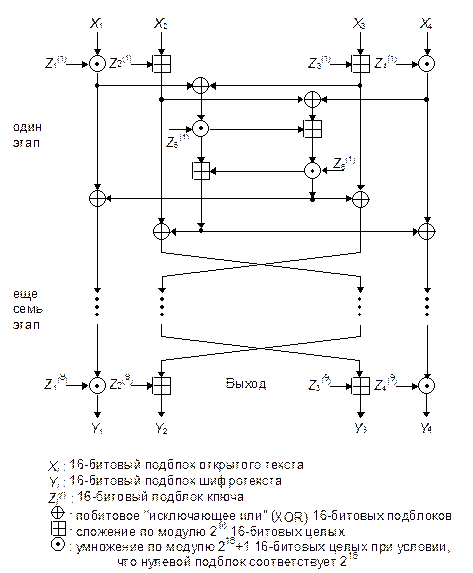
Рис. 13-9. IDEA.
Выходом этапа являются четыре подблока - результаты действий (11), (12), (13) и (14). Поменяйте местами два внутренних подблока (но не в последнем этапе), и вы получите исходные данные для следующего этапа.
После восьмого этапа выполняется заключительное преобразование:
(1) Перемножаются Xl и первый подключ.
(2) Складываются X2 и второй подключ.
(3) Складываются X3 и третий подключ.
(4) Перемножаются X4 и четвертый подключ.
Наконец четыре подблока снова соединяются, образуя шифротекст.
Также несложно создавать подключи. Алгоритм использует 52 из них (шесть для каждого из восьми этапов и еще четыре для заключительного преобразования). Сначала 128-битовый ключ делится на восемь 16-битовых подключей. Это первые восемь подключей алгоритма (шесть для первого этапа и два - для второго). Затем ключ циклически сдвигается налево на 25 битов и снова делится на восемь подключей. Первые четыре используются на этапе 2, а оставшиеся четыре - на этапе 3. Ключ циклически сдвигается налево на 25 битов для получения следующих восьми подключей, и так до конца алгоритма.
Дешифрирование выполняется точно также за исключением того, что подключи инвертируются и слегка изменяются. Подключи при дешифрировании представляют собой обратные значения ключей шифрования по отношению к операциям либо сложения, либо умножения. (Для IDEA подблоки, состоящие из одних нулей, считаются равными 216 = -1 для умножения по модулю 216 + 1, следовательно, обратным значением 0 относительно умножения является 0.) Эти вычисления могут занять некоторое время, но их нужно выполнить один раз для каждого ключа дешифрирования. В Табл. 13-4 представлены подключи шифрования и соответствующие подключи дешифрирования.
Табл. 13-4.
Подключи шифрования и дешифрирования IDEA
| Этап | Подключи шифрования | Подключи дешифрирования | ||||||||||||||
| Z1(1) | Z2(1) | Z3(1) | Z4(1) | Z5(1) | Z6(1) | Z1(9)-1 | -Z2(9) | -Z3(9) | Z4(9)-1 | Z5(8) | Z6(8) | |||||
| Z1(2) | Z2(2) | Z3(2) | Z4(2) | Z5(2) | Z6(2) | Z1(8)-1 | -Z2(8) | -Z3(8) | Z4(8)-1 | Z5(7) | Z6(7) | |||||
| Z1(3) | Z2(3) | Z3(3) | Z4(3) | Z5(3) | Z6(3) | Z1(7)-1 | -Z2(7) | -Z3(7) | Z4(7)-1 | Z5(6) | Z6(6) | |||||
| Z1(4) | Z2(4) | Z3(4) | Z4(4) | Z5(4) | Z6(4) | Z1(6)-1 | -Z2(6) | -Z3(6) | Z4(6)-1 | Z5(5) | Z6(5) | |||||
| Z1(5) | Z2(5) | Z3(5) | Z4(5) | Z5(5) | Z6(5) | Z1(5)-1 | -Z2(5) | -Z3(5) | Z4(5)-1 | Z5(4) | Z6(4) | |||||
| Z1(6) | Z2(6) | Z3(6) | Z4(6) | Z5(6) | Z6(6) | Z1(4)-1 | -Z2(4) | -Z3(4) | Z4(4)-1 | Z5(3) | Z6(3) | |||||
| Z1(7) | Z2(7) | Z3(7) | Z4(7) | Z5(7) | Z6(7) | Z1(3)-1 | -Z2(3) | -Z3(3) | Z4(3)-1 | Z5(2) | Z6(2) | |||||
| Z1(8) | Z2(8) | Z3(8) | Z4(8) | Z5(8) | Z6(8) | Z1(2)-1 | -Z2(2) | -Z3(2) | Z4(2)-1 | Z5(1) | Z6(1) | |||||
| заключительное преобразование | Z1(9) | Z2(9) | Z3(9) | Z4(9) | Z1(1)-1 | -Z2(1) | -Z3(1) | Z4(1)-1 | ||||||||
Скорость IDEA
Современные программные реализации IDEA примерно в два раза быстрее, чем DES. На компьютере с i386/33 МГц IDEA шифрует данные со скоростью 880 Кбит/с, а на компьютере с i486/33 МГц - со скоростью 2400 Кбит/с. Вы могли подумать, что IDEA должен был быть побыстрее, но умножения - недешевое удовольствие. Умножение двух 32-битовых чисел на процессоре i486 занимает 40 тактов (10 на процессоре Pentium).
Реализация PES на базе СБИС шифрует данные со скоростью 55 Мбит/с при тактовой частоте 25 МГц [208,398]. Другая СБИС, разработанная ETH Zurich и состоящая из of 251000 транзисторов на кристалле площадью 107.8 мм2, шифрует данные с помощью алгоритма IDEA со скоростью 177 Мбит/с при тактовой частоте 25 МГц [926, 207, 397].
Криптоанализ IDEA
Длина ключа IDEA равна 128 битам - более чем в два раза длиннее ключа DES. При условии, что наиболее эффективным является вскрытие грубой силой, для вскрытия ключа потребуется 2128 (1038) шифрований. Создайте микросхему, которая может проверять миллиард ключей в секунду, объедините миллиард таких микросхем, и вам потребуется 1013 лет для решения проблемы - это больше, чем возраст вселенной. 1024 таких микросхем могут найти ключ за день, но во вселенной не найдется столько атомов кремния, чтобы построить такую машину. Наконец мы чего-то достигли, хотя в некоторых темных вопросах я лучше останусь сторонним наблюдателем.
Может быть вскрытие грубой силой - не лучший способ вскрытия IDEA. Алгоритм все еще слишком нов, чтобы можно было говорить о каких-то конкретных криптографических результатах. Разработчики сделали все возможное, чтобы сделать алгоритм устойчивым к дифференциальному криптоанализу. Они определили понятие марковского шифра и продемонстрировали, что устойчивость к дифференциальному криптоанализу может быть промоделирована и оценена количественно [931, 925]. (Для сравнения с алгоритмом IDEA, устойчивость которого к дифференциальному криптоанализу была усилена, и который показан на Рис. 13-9, на Рис. 13-10 приведен первоначальный алгоритм PES. Удивительно, как такие незначительные изменения могут привести к столь большим различиям.) В [925] Лай (Lai) утверждал (он привел подтверждение, но не доказательство), что IDEA устойчив к дифференциальному криптоанализ уже после 4 из 8 этапов. Согласно Бихаму, его попытка вскрыть IDEA с помощью криптоанализа со связанными ключами также не увенчалась успехом [160].
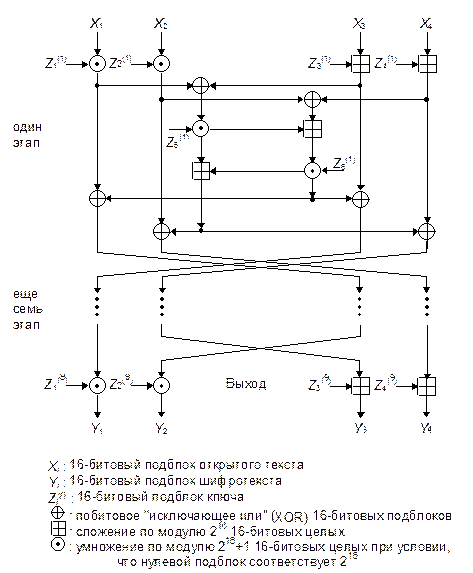
Рис. 13-10. PES.
Вилли Майер (Willi Meier) исследовал три алгебраических операции IDEA и показал, что, хотя они несовместимы, есть случаи, когда эти операции можно упростить так, чтобы в некоторой степени облегчить [1050]. Его вскрытие 2-этапного IDEA оказалось эффективнее вскрытия грубой силой (242 операций), но для IDEA с 3 и более этапами эффективность этого вскрытия была ниже вскрытия грубой силой. Безопасность полного 8-этапного IDEA осталась непоколебимой.
Джоан Дэймен (Joan Daemen) открыла класс слабых ключей IDEA [405, 409]. Эти ключи не являются слабыми в том смысле, в котором слабы некоторые ключи DES, для которых функция шифрования обратна самой себе. Слабость этих ключей состоит в том, что взломщик может легко определить их с помощью вскрытия с выбранным открытым текстом. Например, слабым является следующий ключ (в шестнадцатиричной записи):
0000,0000,0x00,0000,0000,000x,xxxx,x000
В позиции "x" может стоять любая цифра. При использовании такого ключа побитовое XOR определенных пар открытых текстов равно побитовому XOR получившихся пар шифротекстов.
В любом случае вероятность случайной генерации одного из таких слабых ключей очень мала: 1/296. Опасность случайно выбрать такой ключ практически не существует. К тому же, несложно модифицировать IDEA так, чтобы исключить наличие слабых ключей - достаточно выполнить XOR каждого подключа с числом 0x0dae [409].
Хотя попыток выполнить криптоанализ IDEA было много, мне неизвестно ни об одной успешной.
Режимы работы и варианты IDEA
IDEA может работать в любом из режимов работы блочного шифра, описанных в главе 9. Против двойных реализаций IDEA может быть предпринято то же вскрытие "встреча посередине", что и против DES (см. раздел 15.1). Однако, так как ключ IDEA более чем в два раза длиннее ключа DES, это вскрытие непрактично. Объем нужной для такого вскрытия памяти составит 64*2128 битов, или 1039 байтов. Может быть во вселенной и достаточно материи, чтобы построить такое хранилище, но я в этом сомневаюсь.
Если вы учитываете возможность использования параллельной вселенной, используйте утроенную реализацию IDEA (см. раздел 15.2):
Такая реализация устойчива против вскрытия "встреча посередине".
Кроме того, почему бы вам не реализовать IDEA независимыми подключами, особенно если ваши средства распределения ключей позволяют работать с длинными ключами. Для IDEA нужно всего 52 16-битовых ключа, общей длиной 832 битов. Этот вариант определенно безопасней, но никто не сможет сказать насколько.
В наивной модификации может быть увеличен вдвое размер блока. Алгоритм также прекрасно работал бы с 32-битовыми подблоками вместо 16-битовых и с 256-битовым ключом. Шифрование выполнялось бы быстрее, и безопасность возросла бы в 232 раза. Или нет? Теория, на которой основан алгоритм, опирается на то, что 216+1 является простым числом. А 232 + 1 простым числом не является. Может быть алгоритм и можно изменить так, чтобы он работал, но его безопасность будет совсем иной. Лай говорит, что заставить работать такой алгоритм будет нелегко [926].
Хотя IDEA кажется намного безопаснее DES, не всегда можно легко заменить один алгоритм другим в существующем приложении. Если ваша база данных и шаблоны сообщений могут работать с 64-битовым ключом, реализация 128-битового ключа IDEA может быть возможной.
Для таких приложений создайте 128-битовый ключ, объединив 64-битовый ключ сам с собой. Не забывайте, что эта модификация заметно ослабляет IDEA.
Если вас больше волнует скорость работы, а не безопасность, попробуйте вариант IDEA с меньшим числом этапов. Сегодня лучшее вскрытие IDEA быстрее вскрытия грубой силой только для 2.5 и менее этапов [1050], 4‑этапный IDEA будет в два раза быстрее и, насколько мне известно, его безопасность не уменьшится.
Caveat Emptor[3]
IDEA - это относительно новый алгоритм, многие вопросы пока остаются открытыми. Образует ли IDEA группу? (Лай думает, что нет [926].) Не существует ли пока не открытых способов вскрытия этого шифра? У IDEA твердая теоретическая основа, но снова и снова казавшиеся безопасными алгоритмы капитулируют перед новыми формами криптоанализа. Ряд групп академических и военных исследователей не опубликовали свои результаты криптоанализа IDEA. Возможно, кто-нибудь уже добился или когда-нибудь добьется успеха.
Патенты и лицензии
IDEA запатентован в Европе и Соединенных Штатах [1012, 1013]. Патент принадлежит Ascom-Tech AG. Для некоммерческого использования лицензирование не нужно. При заинтересованности в лицензии для коммерческого применения алгоритма следует обратиться по адресу Ascom Systec AG, Dept CMVV, Cewerbepark, CH-5506, Mgenwil, Switzerland; +41 64 56 59 83; Fax: +41 64 56 59 90; idea@ascom.ch.
MMB
Недовольство использованием в IDEA 64-битового блока шифрования привело к созданию Джоном Дэймоном алгоритма под названием MMB (Modular Multiplication-based Block cipher, модульный блочный шифр, использующий умножения) [385, 405, 406]. В основе MMB лежит теория, используемая и в IDEA: перемешивающие операции из различных групп. MMB - это итеративный алгоритм, главным образом состоящий из линейных действий (XOR и использование ключа) и параллельное использование четырех больших нелинейных изменяющих обычный порядок подстановок. Эти подстановки определяются с помощью умножения по модулю 232‑1 с постоянными множителями. Результатом применения этих действий является алгоритм, использующий и 128-битовый ключ и 128-битовый блок.
MMB оперирует 32-битовыми подблоками текста (x0, x1, x2, x3) и 32-битовыми подблоками ключа (k0, k1, k2, k3). Это делает удобным реализацию алгоритма на современных 32-битовых процессорах. Чередуясь с XOR, шесть раз используется нелинейная функция f. Вот этот алгоритм (все операции с индексами выполняются по модулю 3):
xi = xi Å ki, для i = 0 до 3
f(x0, x1, x2, x3)
xi = xi Å ki+1, для i = 0 до 3
f(x0, x1, x2, x3)
xi = xi Å ki+2, для i = 0 до 3
f(x0, x1, x2, x3)
xi = xi Å ki, для i = 0 до 3
f(x0, x1, x2, x3)
xi = xi Å ki+1, для i = 0 до 3
f(x0, x1, x2, x3)
xi = xi Å ki+2, для i = 0 до 3
f(x0, x1, x2, x3)
У функции f три этапа:
(1) x1 = ci * xi, для i = 0 до 3 (Если на входе умножения одни единицы, то на выходе - тоже одни единицы.)
(2) Если младший значащий бит x0 = 1, то x0 = x0 Å C. Если младший значащий бит x3 = 0, то x3 = x3 Å C.
(3) xi = xi-1 Å xi Å xi+1, для i = 0 до 3
Все операции с индексами выполняются по модулю 3. Операция умножения на этапе (1) выполняется по модулю 232-1. В данном алгоритме если второй операнд - это 232-1, то результат также равен 232-1. В алгоритме используются следующие константы:
C = 2aaaaaaa
c0 = 025f1cdb
cl = 2 * c0
c2= 23 * c0
c3 = 27 * c0
Константа C - это "простейшая" константа с высоким троичным весом, нулевым младшим значащим битом и без круговой симметрии. У константы c0 несколько иные характеристики. Константы cl, c2 и c3 являются смещенными версиями c0, и используются для предотвращения вскрытий основанных на симметрии. Подробности можно найти в [405].
Дешифрирование является обратным процессом. Этапы (2) и (3) заменяются на свою инверсию. На этапе (1) вместо ci-1 используется ci. ci-1 = 0dad4694.
Безопасность MMB
Схема MMB обеспечивает на каждом этапе значительное и независимое от ключа рассеяние. В IDEA рассеяние до определенной степени зависит от конкретных подключей. В отличие от IDEA у MMB нет слабых ключей.
К сожалению MMB - это умерший алгоритм [402]. Это утверждение справедливо по многим причинам, хотя криптоанализ MMB и не был опубликован. Во первых, он проектировался без учета требований устойчивости к линейному криптоанализу. Выбор мультипликативных множителей обеспечил устойчивость к дифференциальному криптоанализу, но о линейном криптоанализе авторам алгоритма было еще неизвестно.
Во вторых, Эли Бихам реализовал эффективное вскрытие с выбранным ключом [160], использующеее тот факт, что все этапы идентичны, а ключ при использовании просто циклически сдвигается на 32 бита. В третьих, несмотря на то, что программные реализации MMB были бы очень эффективны, в аппаратном исполнении алгоритм менее эффективен, чем DES.
Дэймон предлагает, что тот, кто захочет улучшить MMB, должен сначала проанализировать умножение по модулю с помощью линейного криптоанализа и подобрать новый множитель, а затем сделать константу C различной для каждого этапа [402]. Затем, улучшив использование ключа, добавляя к ключам этапов константы с целью устранения смещения. Но сам не стал заниматься этим и разработал 3-Way (см. раздел 14.5).
CA-1.1
CA - это блочный шифр, основанный на клеточных автоматах и разработанный Говардом Гутовицом (Howard Gutowitz) [677, 678, 679]. Он шифрует 384-битовые блоки открытого текста 1088-битовым ключом (на самом деле используется два ключа - 1024-битовый и 64- битовый). Из-за природы клеточных автоматов алгоритм наиболее эффективен при реализации в больших параллельных интегрированных схемах.
CA-1.1 использует как обратимые, так и необратимые правила клеточного автомата. При обратимом правиле каждое состояние структуры получается из единственного предшествующего состояния, а при необратимом правиле у каждого состояния может быть несколько предшественников. При шифровании необратимые правила пошагово обращаются во времени. Для продвижения обратно от текущего состояния случайным образом должно выбираться одно из состояний-предшественников. Этот процесс многократно повторяется. Таким образом, обратная итерация служит для смешивания случайной информации с инфорамацией сообщения. CA-1.1 использует особый сорт частично линейного необратимого правила, такого, что для любого данного состояния может быть быстро построено случайное состояние-предшественник. На некоторых стадиях шифрования используются и обратимые правила.
Обратимые правила (простые параллельные перестановки подблоков состояния) нелинейны. Необратимые правила полностью определяются ключом, а обратимые зависят как от ключа, так и от случайной информации, вставленной в ходе шифрования необратимыми правилами.
CA-1.1 основан на структуре блочных связей. То есть, обработка блока сообщения частично отделена от обработки потока случайной информации, вставленной при шифровании. Эта случайная информация служит для связи друг с другом стадий шифрования. Она также может быть использована для связи с потоком шифротекста. Информация связи генерируется как часть шифрования.
Так как CA-1.1 представляет собой новый алгоритм, слишком рано делать какие-либо заявления о его безопасности. Гутовиц упоминает некоторые возможные вскрытия, включая дифференциальный криптоанализ, но ему не удалось вскрыть алгоритм. В качестве стимула Гутовиц предложил награду в 1000 долларов для "первого человека, который разработает доступную процедуру вскрытия CA-1.1."
CA-l.1 запатентован [678], но доступен для некоммерческого использования. При необходимости получить лицензию на алгоритм или объявленную награду за криптоанализ обращайтесь к Говарду Гутовицу по адресу Howard Cutowitz, ESPCI, Laboratorie d'Electronique, 10 rue Vauquelin, 75005 Paris, France.
SKIPJACK
Skipjack разработан NSA в качестве алгоритма шифрования для микросхем Clipper и Capstone (см. разделы 24.16 и 24.17). Так как этот алгоритм объявлен секретным, его подробности никогда не публиковались. Он будет реализован только как защищенная от взлома аппаратура.
Этот алгоритм объявлен секретным не потому, что это повышает его надежность, а потому что NSA не хочет, чтобы Skipjack использовался без механизма условного вручения ключей Clipper. Агентство не хочет, чтобы программные реализации алгоритма распространились по всему миру.
Безопасен ли Skipjack? Если NSA захочет создать безопасный алгоритм, оно, скорее всего, это сделает. С другой стороны, если NSA захочет создать алгоритм с лазейкой, то оно сможет сделать и это. Вот что было опубликовано [1154, 462].
— Это итеративный блочный шифр.
— Размер блока - 64 бита.
— Алгоритм использует 80-битовый ключ.
— Он может быть использован в режимах ECB, CBC, 64-битовый OFB, либо 1-, 8-, 16-, 32- или 64-битовый CFB.
— Операция шифрования или дешифрирования состоит из 32 этапов.
— NSA начало работу над ним в 1985 и завершило проверку в 1990.
В документации на микросхему Mykotronx Clipper утверждается, что задержка в выдаче результата, присущая алгоритму Skipjack, составляет 64 такта. Это означает, что на каждый этап приходится два такта: один предположительно для подстановки с помощью S-блока, а другой - для заключительного XOR в конце каждого этапа. (Не забывайте, перестановки при аппаратных реализациях не занимают времени.) В документации Mykotronx эта двухтактная операция называется "G-блоком", а все вместе - "сдвигом". (Часть G-блока носит название "F-таблицы" и является таблицей констант, а может быть таблицей функций.)
По одним слухам Skipjack использует 16 S-блоков, а по другим для хранения S-блоков нужно всего 128 байт памяти. Непохоже, чтобы оба этих слуха были правдой.
Еще один слух утверждает, что этапы Skipjack, в отличие от DES, работают не с половиной блока. Это вместе с замечанием о "сдвигах" и случайном заявлении на Crypto '94 о том, что в Skipjack применяется "48-битовая внутренняя структура", позволяет сделать вывод, что алгоритм по своей схеме похож на SHA (см. раздел 18.7), но использует четыре 16-битовых подблока. Три подблока, обработанные зависящей от ключа однонаправленной функцией, дают 16 битов, которые подвергаются операции XOR с оставшимся подблоком. Затем весь блок циклически сдвигается на 16 битов и поступает на вход следующего этапа, или сдвига. При этом также используются 128 байтов данных S-блока. Я подозреваю, что S-блоки зависят от ключа.
По своей структуре Skipjack вероятно похож на DES. NSA понимает, что его защищенная от взлома аппаратура в конце концов будет вскрыта и исследована, они не будут рисковать никаким
Дата добавления: 2021-01-26; просмотров: 729;











