Потоковые шифры на базе LFSR

<65 66 676869 70 71 >

Основной подход при проектировании генератора потока ключей на базе LFSR прост. Сначала берется один или несколько LFSR, обычно с различными длинами и различными многочленами обратной связи. (Если длины взаимно просты, а все многочлены обратной связи примитивны, то у образованного генератора будет максимальная длина.) Ключ является начальным состоянием регистров LFSR. Каждый раз, когда необходим новый бит, сдвиньте на бит регистры LFSR (это иногда называют тактированием (clocking)). Бит выхода представляет собой функцию, желательно нелинейную, некоторых битов регистров LFSR. Эта функция называется комбинирующей функцией, а генератор в целом - комбинационным генератором. (Если бит выхода является функцией единственного LFSR, то генератор называется фильтрующим генератором.) Большая часть теории подобного рода устройств разработана Селмером (Selmer) и Нилом Цирлером (Neal Zierler) [1647].

Можно ввести ряд усложнений. В некоторых генераторах для различных LFSR используется различная тактовая частота, иногда частота одного генератора зависит от выхода другого. Все это электронные версии идей шифровальных машин, появившихся до Второй мировой войны, которые называются генераторами с управлением тактовой частотой (clock-controlled genelators) [641]. Управление тактовой частотой может быть с прямой связью, когда выход одного LFSR управляет тактовой частотой другого LFSR, или с обратной связью, когда выход одного LFSR управляет его собственной тактовой частотой.

Хотя все эти генераторы чувствительны, по крайней мере теоретически, к вскрытиям вложением и вероятной корреляцией [634, 632], многие из них безопасны до сих пор. Дополнительную теорию сдвиговых регистров с управляемой тактовой частотой можно найти в [89].

Ян Касселлс (Ian Cassells), ранее возглавлявший кафедру чистой математики в Кембридже и работавший криптоаналитиком в Bletchly Park, сказал, что "криптография - это смесь математики и путаницы, и без путаницы математика может быть использована против вас." Он имел в виду, что в потоковых шифрах для обеспечения максимальной длины и других свойств необходимы определенные математические структуры, такие как LFSR, но, чтобы помешать кому-то получить содержание регистра и вскрыть алгоритм, необходимо внести некоторый сложный нелинейный беспорядок. Этот совет справедлив и для блочных алгоритмов.

Поэтому не стоит серьезно увлекаться генераторами потока ключей на базе LFSR, описания которых появились в литературе. Я не знаю, используется ли хоть один из них в реальных криптографических продуктах. Большей частью они представляют лишь теоретический интерес. Некоторые были взломаны, некоторые могли остаться безопасными.

Так как шифры на базе LFSR обычно реализуются аппаратно, на рисунках используются символы электронной логики. В тексте, Å означает XOR, Ù - AND, Ú - OR, и Ø - NOT.

Генератор Геффа

В этом генераторе потока ключей используются три LFSR, объединенные нелинейным образом (см. Рис. 16-6) [606]. Два LFSR являются входами мультиплексора, а третий LFSR управляет выходом мультиплексора. Если a₁, a₂ и a₃ - выходы трех LFSR, выход генератора Геффа (Geffe) можно описать как:

b= (a₁ Ù a₂) Å((Øa₁) Ù a₃)

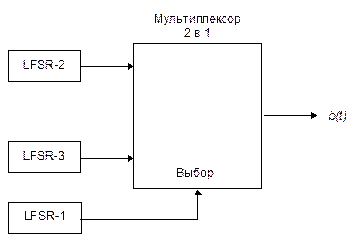
Рис. 16-6. Генератор Геффа.

Если длины LFSR равны n₁, n₂ и n₃, соответственно, то линейная сложность генератора равна

(n₁+ 1) n₂ + n₁n₃,

Период генератора равен наименьшему общему делителю периодов трех генераторов. При условии, что степени трех примитивных многочленов обратной связи взаимно просты, период этого генератора будет равен произведению периодов трех LFSR.

Хотя этот генератор неплохо выглядит на бумаге, он криптографически слаб и не может устоять против корреляционного вскрытия [829, 1638]. В 75 процентах времени выход генератора равен выходу LFSR-2. Поэтому, если известны отводные последовательности обратной связи, можно догадаться о начальном значении LFSR-2 и сгенерировать выходную последовательность этого регистра. Тогда можно подсчитать, сколько раз выход LFSR совпадает с выходом генератора. Если начальное значение определено неверно, две последовательности будут согласовываться в 50 процентах времени, а если правильно, то в 75 процентах времени.

Аналогично, выход генератора равен выходу LFSR в 75 процентах времени. С такими корреляциями генератор потока ключей может быть легко взломан. Например, если примитивные многочлены состоят только из трех членов, и длина самого большого LFSR равна n, для восстановления внутренних состояний всех трех LFSR нужен фрагмент выходной последовательности длиной 37n битов [1639].

Обобщенный генератор Геффа

Вместо выбора между двумя LFSR в этой схеме выбирается один из kLFSR, где kявляется степенью 2. Всего используется k+ 1 LFSR (см. Рис. 16-7). Тактовая частота LFSR-l должна быть в log₂ k раз выше, чем у остальных kLFSR.

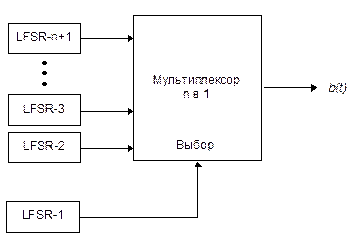
Рис. 16-7. Обобщенный генератор Геффа.

Несмотря на то, что эта схема сложнее генератора Геффа, для взлома можно использовать то же корреляционное вскрытие. Не рекомендую этот генератор.

Генератор Дженнингса

В этой схеме мультиплексор используется для объединения двух LFSR [778, 779, 780]. Мультиплексор, управляемый LFSR-l, выбирает 1 бит LFSR-2 в качестве очередного выходного бита. Кроме того, используется функция, которая отображает выход LFSR-2 на вход мультиплексора (см. Рис. 16-8).

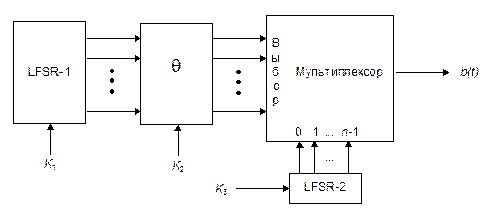
Рис. 16-8. Генератор Дженнингса.

Ключом является начальное состояние двух LFSR и функции отображения. Хотя у этого генератора замечательные статистические свойства, он пал перед выполненным Россом Андерсоном (Ross Anderson) вскрытием корректности встречей посередине [39] и вскрытием линейной корректности [1638,442]. Не используйте этот генератор.

Генератор "стоп-пошел" (Stop-and-Go) Both-Piper

Этот генератор, показанный на Рис. 16-9, использует выход одного LFSR для управления тактовой частотой другого LFSR [151]. Тактовый вход LFSR-2 управляется выходом LFSR-l, так что LFSR-2 может изменять свое состояние в момент времени tтолько, если выход LFSR-l в момент времени t- 1 был равен 1.

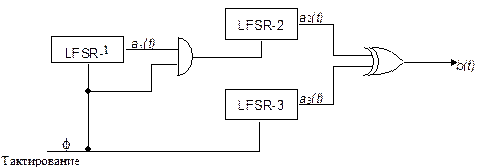
Рис. 16-9. Генератор "стоп-пошел" Beth-Piper.

Никому не удалось привести для общего случая достоверные данные о линейной сложности этого генератора. Однако он не устоял перед корреляционным вскрытием [1639].

Чередующийся генератор "стоп-пошел"

В этом генераторе используются три LFSR различной длины. LFSR-2 тактируется, когда выход LFSR-l равен 1, LFSR-3 тактируется, когда выход LFSR-l равен 0. Выходом генератора является XOR LFSR-2 и LFSR-3 (см. Рис. 16.10) [673].

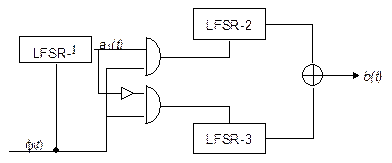
Рис. 16-10. Чередующийся генератор "стоп-пошел"

У этого генератора большой период и большая линейная сложность. Авторы показали способ корреляционного вскрытия LFSR-1, но это не сильно ослабляет генератор. Были предложены и другие генераторы такого типа [1534, 1574, 1477].

Двусторонний генератор "стоп-пошел"

В этом генераторе используется два LFSR с одинаковой длиной n(см. Рис. 16.11) [1638]. Выходом генератора является XOR выходов каждого LFSR. Если выход LFSR-l в момент времени t-1 равен 0, а в момент времени t-2 - 1, то LFSR-2 не тактируется в момент времени t. Наоборот, если выход LFSR-2 в момент времени t-1 равен 0, а в момент времени t-2 - 1, и если LFSR-2 тактируется в момент времени t, то LFSR-l не тактируется в момент времени t.

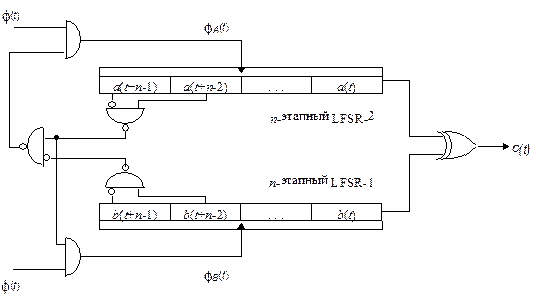
Рис. 16-11. Двусторонний генератор "стоп-пошел".

Линейная сложность такой системы примерно равна ее периоду. Согласно [1638], "в такой системе не очевидная избыточность ключа не наблюдается".

<65 66 676869 70 71 >

Дата добавления: 2021-01-26; просмотров: 524;