Тройное шифрование с двумя ключами

В более интересном методе, предложенном Тачменом в [1551], блок обрабатывается три раза с помощью двух ключей: первым ключом, вторым ключом и снова первым ключом. Он предлагает, чтобы отправитель сначала шифровал первым ключом, затем дешифрировал вторым, и окончательно шифровал первым ключом. Получатель расшифровывает первым ключом, затем шифрует вторым и, наконец, дешифрирует первым.

Иногда такой режим называют шифрование-дешифрирование-шифрование (encrypt-decrypt-encrypt, EDE) [55]. Если блочный алгоритм использует n-битовый ключ, то длина ключа описанной схемы составляет 2n бит. Любопытный вариант схемы шифрование-дешифрирование-шифрование был разработан в IBM для совместимости с существующими реализациями алгоритма: задание двух одинаковых ключей эквивалентно одинарному шифрованию. этим ключом. Схема шифрование-дешифрирование-шифрование сама по себе не обладает никакой безопасностью, но этот режим был использован для улучшения алгоритма DES в стандартах X9.17 и ISO 8732 [55, 761].

K₁и K₂ чередуются для предотвращения описанного выше вскрытия "встреча посередине". Если 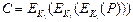, то криптоаналитик для любого возможного K₁может заранее вычислить 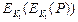и затем выполнить вскрытие. Для этого потребуется только 2ⁿ⁺² шифрований.

Тройное шифрование с двумя ключами устойчиво к такому вскрытию. Но Меркл и Хеллман разработали другой способ размена памяти на время, который позволяет взломать этот метод шифрования за 2^n-1 действий, используя 2ⁿ блоков памяти [1075].

Для каждого возможного K₂ расшифруйте 0 и сохраните результат. Затем расшифруйте 0 для каждого возможного K₁, чтобы получить P. Выполните тройное шифрование P, чтобы получить C, и затем расшифруйте Cключом K₁. Если полученное значение совпадает с значением (хранящемся в памяти), полученным при дешифрировании 0 ключом K₂, то пара K₁ K₂ является возможным результатом поиска. Проверьте, так ли это. Если нет, продолжайте поиск.

Выполнение этого вскрытия с выбранным открытым текстом требует огромного объема памяти. Понадобится 2ⁿ времени и памяти, а также 2^m выбранных открытых текстов. Вскрытие не очень практично, но все же чувствительность к нему является слабостью алгоритма.

Пауль ван Оорсчот (Paul van Oorschot) и Майкл Винер (Michael Wiener) преобразовали это вскрытие ко вскрытию с известным открытым текстом, для которого нужно p известных открытых текстов. В примере предполагается, что используется режим EDE.

(1) Предположить первое промежуточное значения a.

(2) Используя известный открытый текст, свести в таблицу для каждого возможного K₁ второе промежуточное значение b, при первом промежуточном значении, равном a:

b =

где C- это шифротекст, полученный по известному открытому тексту.

(3) Для каждого возможного K₂ найти в таблице элементы с совпадающим вторым промежуточным значение b:

b=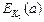

(4) Вероятность успеха равно p/m, где p- число известных открытых текстов, а m- размер блока. Если совпадения не обнаружены, выберите другое aи начните сначала.

Вскрытие требует 2^n+m/p времени и p - памяти. Для DES это равно 2¹²⁰/p [1558]. Для p, больших 256, это вскрытие быстрее, чем исчерпывающий поиск.