Построение точки пересечения прямой с плоскостью
Решается с помощью вспомогательной секущей плоскости.
Алгоритм решения:
1) Заданная прямая заключается во вспомогательную плоскость. В качестве вспомогательной чаще всего используются проецирующие плоскости.
2) Строится прямая пересечения вспомогательной плоскости с заданной плоскостью.
3) Построенная прямая и заданная прямая будут лежать во вспомогательной плоскости, Þ будут пересекаться. Точка их пересечения будет являться искомой точкой пересечения заданной прямой и заданной плоскости.
4) После нахождения точки пересечения нужно определить видимость прямой относительно плоскости.
Пример.
Построить точку пересечения прямой l и плоскости S(АВС).

1. Построение прямой пересечения двух плоскостей
Две плоскости пересекаются по прямой.
Т.к. прямая определяется двумя точками, достаточно найти 2 точки Î прямой пересечения. Для этого надо провести 2 вспомогательные секущие плоскости.
1) Проводится вспомогательная плоскость (проецирующая или уровня).
2) Строятся прямые пересечения вспомогательной плоскости с каждой из заданных плоскостей.
3) Находится точка пересечения построенных прямых,
4) Для нахождения второй точки прямой пересечения нужно провести вторую вспомогательную плоскость и выполнить аналогичные построения.
Пример.
Построить прямую пересечения плоскости S( 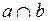 ) и Q(
) и Q( 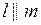 )
)
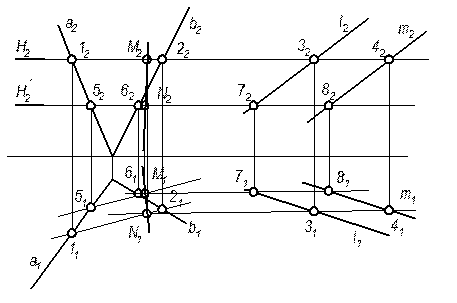
| 1) H(H2)
2) 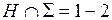
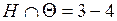 3)
3) 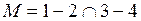 4)
4) 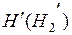 5)
5) 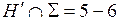
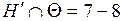 6)
6) 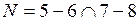
|
2. Пересечение поверхности плоскостью
При пересечении плоскости с поверхностью искомая линия пересечения будет представлять собой плоскую кривую. Сложность решения задачи зависит от того, какая задана плоскость – частного положения или общего.
Дата добавления: 2016-10-26; просмотров: 5093;











