Определение наименьшего и наибольшего значения функции на промежутке

Непрерывная функция задана на закрытом промежутке (отрезке).

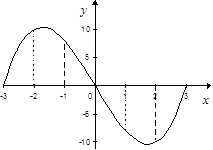
Рассмотрим для примера график функции 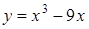. На промежутке 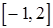наибольшее значение функции достигается на левом конце промежутка при 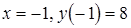; наименьшее – в точке минимума при .

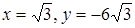Если взять промежуток 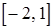, то наибольшее значение достигается в точке максимума при 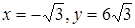, а наименьшее – на правом конце промежутка при 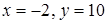. На промежутке 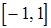наибольшее значение функции на левом конце при 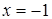, наименьшее – на правом при .

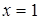Следовательно, в зависимости от выбранного промежутка изменения переменной x наибольшее или наименьшее значение непрерывной функции может достигаться или на концах промежутка, или в точках экстремума.

Итак, чтобы найти наибольшее или наименьшее значение непрерывной функции на отрезке, нужно найти производную функции и определить ее критические точки. Затем вычислить значения функции на концах промежутка и в тех критических точках, которые попадают на промежуток. Из полученных значений выбрать наибольшее и наименьшее значение.