ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 7 глава

Наиболее широко гаммирование используется для криптографического закрытия сообщений, уже выраженных в двоичном коде.

В этом случае особенно просто реализуется устройство, вырабатывающее ключ. Оно представляет собой регистр сдвига с обратными связями. Соответствующим выбором обратных связей можно добиться генерирования двоичных последовательностей, период повторения которых составляет 2ⁿ-1 символов, где n — число разрядов регистра. Такие последовательности называют псевдослучайными. С одной стороны, они удовлетворяют ряду основных тестов на случайность, что существенно затрудняет раскрытие такого ключа, а с другой — являются детерминированными, что позволяет обеспечить однозначность дешифрования сообщения. Подробно регистры с обратными связями рассмотрены в § 6.8.

Надежность криптографического закрытия методом гаммирования определяется главным образом длиной неповторяющейся части гаммы. Если она превышает длину закрываемого текста, то раскрыть криптограмму, опираясь только на результаты статистической обработки этого текста, теоретически невозможно.

Однако если удастся получить некоторое число двоичных символов исходного текста и соответствующих им двоичных символов криптограммы, то сообщение нетрудно раскрыть, так как преобразование, осуществляемое при гаммировании, является линейным. Для полного раскрытия достаточно всего 2n двоичных символов зашифрованного и соответствующего ему исходного текста.

Современный стандартный метод шифрования данных. Рассмотрим теперь метод криптографического закрытия данных, удовлетворяющий всем указанным ранее требованиям. Он является действующим стандартом шифрования данных в США и удобен для защиты информации как при передаче данных, так и при их хранении в запоминающих устройствах [6].

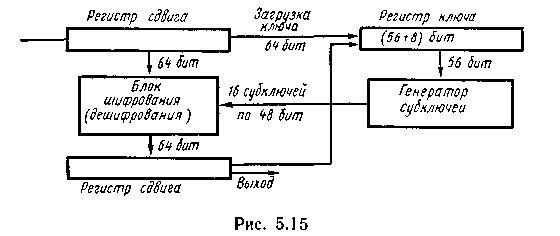В процессе шифрования последовательность символов определенной длины (64 бит) преобразуется в шифрованный блок той же длины. Операции шифрования и дешифрования осуществляются по схеме, представленной на рис. 5.15.

Перед началом шифрования в специализированный регистр устройства через входной регистр вводится ключ, содержащий 64 бит, из которых 56 используются для генерации субключей, а 8 являются проверочными. Ключ из устройства вывести нельзя. Предусмотрена возможность формирования нового ключа внутри устройства. При этом ключ, вводимый в устройство, шифруется ранее использовавшимся ключом и затем через выходной регистр вводится в специальный регистр в качестве нового ключа.

16 субключей по 48 бит каждый, сформированных в генераторе субключей, используются для шифрования блока из 64 символов, поступающих во входной регистр устройства. Шифрование осуществляется из 16 логически идентичных шагов, на каждом из которых используется один из субключей.

Процесс дешифрования выполняется по тому же алгоритму, что и процесс шифрования, с той лишь разницей, что субключи генерируются в обратном порядке.

В основе технической реализации такого устройства лежат регистры с обратными связями. В результате коммутации цепей обратной связи регистра-шифратора в соответствии с генерируемыми субключами нарушается линейность преобразования входной последовательности, что и обеспечивает высокую надежность криптографического закрытия данных.

§ 5.4. ЭФФЕКТИВНОЕ КОДИРОВАНИЕ

Как отмечалось, в большинстве случаев знаки сообщений преобразуются в последовательности двоичных символов. В рассмотренных устройствах это преобразование выполнялось без учета статистических характеристик поступающих сообщений.

Учитывая статистические свойства источника сообщения, можно минимизировать среднее число символов, требующихся для выражения одного знака сообщения, что при отсутствии шума позволяет уменьшить время передачи или объем запоминающего устройства.

Основная теорема Шеннона о кодировании для канала без помех. Эффективное кодирование сообщений для передачи их по дискретному каналу без помех базируется на теореме Шеннона, которую можно сформулировать так:

1. При любой производительности источника сообщений, меньшей пропускной способности канала, т. е. при условии

где ε — сколь угодно малая, положительная величина, существует способ кодирования, позволяющий передавать по каналу все сообщения, вырабатываемые источником.

2. Не существует способа кодирования, обеспечивающего передачу сообщений без их неограниченного накопления, если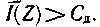

Поскольку строгое математическое доказательство относительно сложно [34], убедимся в справедливости теоремы, основываясь на эвристических соображениях.

В основе доказательства лежит идея возможности повышения скорости передачи информации по каналу, если при кодировании последовательности символов ставить в соответствие не отдельным знакам, а их последовательностям такой длины, при которой справедлива теорема об их асимптотической равновероятности. При этом, естественно, в первую очередь подлежат кодированию типичные последовательности.

Если количество знаков в кодируемой последовательности равно Ν, а энтропия источника — Η(Ζ), то в соответствии с (4.8) число типичных последовательностей

Так как Ν = Τ/τ, где Т — длительность кодируемой последовательности; τ — длительность одного знака, то

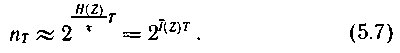
Каждой типичной последовательности нужно поставить в соответствие кодовую комбинацию той же продолжительности Т из символов с объемом алфавита m. При скорости манипуляции V_T число символов в кодовой комбинации составит TV_Т, что позволяет образовать n_k различных кодовых комбинаций, причем

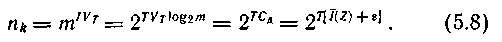
Сравнение (5.7) и (5.8) показывает, что 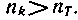Следовательно, если 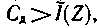то кодовых комбинаций, пропускаемых каналом, достаточно для того, чтобы закодировать все типичные последовательности знаков, причем останется еще некоторый излишек.

Нетипичным последовательностям в принципе могут быть поставлены в соответствие кодовые комбинации со значительно большим числом символов. Для различения эти комбинации в начале и конце сопровождаются кодовыми комбинациями, взятыми из излишка, не использованного для кодирования типичных последовательностей. Однако всем нетипичным последовательностям можно ставить в соответствие и одну и ту же кодовую комбинацию из указанного излишка, предопределяя их недостоверную передачу.

Поскольку при 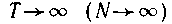вероятность появления нетипичной последовательности стремится к нулю, в первом случае это никак не отразится на эффективности передачи, а во втором — на уровне надежности отождествления принятых комбинаций с действительно переданными.

Отметим, что ограничиваясь кодированием типичных последовательностей, вероятности которых равны, мы обеспечиваем равновероятное и независимое поступление символов на вход канала, что соответствует полному устранению избыточности в передаваемом сообщении.

Справедливость второй части теоремы, указывающей на невозможность осуществления передачи при 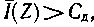следует из определения пропускной способности канала как максимально достижимой скорости передачи информации, взятой по всему множеству источников заданного класса. Поэтому если пропускная способность канала меньше производительности источника, то неизбежно накопление сообщений на передающей стороне.

Рассматриваемая теорема Шеннона часто приводится и в другой формулировке:

сообщения источника с энтропией Η(Ζ) всегда можно закодировать последовательностями символов с объемом алфавита m так, что среднее число символов на знак сообщения l_cр будет сколь угодно близко к величине 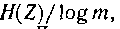но не менее ее.

Данное утверждение обосновывается также указанием на возможную процедуру кодирования, при которой обеспечивается равновероятное и независимое поступление символов на вход канала, а следовательно, и максимальное количество переносимой каждым из них информации, равное log m. Как мы установили ранее, в общем случае это возможно, если кодировать сообщения длинными блоками. Указанная граница достигается асимптотически при безграничном увеличении длины кодируемых блоков.

В частности, при двоичном кодировании (m = 2) среднее число символов на знак сообщения может быть уменьшено до значения, равного энтропии источника, выраженной в дв. ед.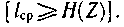

Методы эффективного кодирования некорреляционной последовательности знаков.Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию.

Следовательно, каждый символ должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

Для случая отсутствия статистической взаимосвязи между знаками конструктивные методы построения эффективных кодов были даны впервые американскими учеными Шенноном и Фано. Их методики существенно не различаются и поэтому соответствующий код получил название кода Шеннона — Фано.

Код строят следующим образом: знаки алфавита сообщений выписывают в таблицу в порядке убывания вероятностей. Затем их разделяют на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем знакам верхней половины в качестве первого символа приписывают 0, а всем нижним — 1. Каждую из полученных групп, в свою очередь, разбивают на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одному знаку.

Пример 5.5. Проведем эффективное кодирование ансамбля из восьми знаков, характеристики которого представлены в табл. 5.4.

Таблица 5.4

Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждого знака требуется три двоичных символа. Используя методику Шеннона — Фано, получаем совокупность кодовых комбинаций, приведенных в табл. 5.4.

Так как вероятности знаков представляют собой целочисленные отрицательные степени двойки, то избыточность при кодировании устраняется полностью. Среднее число символов на знак в этом случае точно равно энтропии. Убедимся в этом, вычислив энтропию:

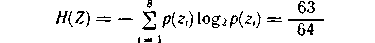
и среднее число символов на знак

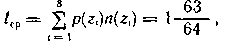
где n(z_i) — число символов в кодовой комбинации, соответствующей знаку z_i.

В более общем случае для алфавита из восьми знаков среднее число символов на знак будет меньше трех, но больше энтропии алфавита Η(Ζ).

Пример 5.6. Определим среднюю длину кодовой комбинации при эффективном кодировании знаков ансамбля, приведенного в табл. 5.5.

Энтропия ансамбля равна 2,76. В результате сопоставления отдельным знакам ансамбля кодовых комбинаций по методике Шеннона — Фано (табл. 5.5) получаем среднее число символов на знак, равное 2,84.

Таблица 5.5

Следовательно, некоторая избыточность в последовательностях символов осталась. Из теоремы Шеннона следует, что эту избыточность также можно устранить, если перейти к кодированию достаточно большими блоками.

Пример 5.7. Рассмотрим процедуру эффективного кодирования сообщений, образованных с помощью алфавита, состоящего всего из двух знаков z₁ и z₂ с вероятностями появления соответственно р(z₁) = 0,9 и ρ(z₂) = 0,1.

Так как вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако при побуквенном кодировании мы никакого эффекта не получим.

Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна 0,47.

При кодировании блоков, содержащих по две буквы, получим коды, показанные в табл. 5.6.

Таблица 5.6

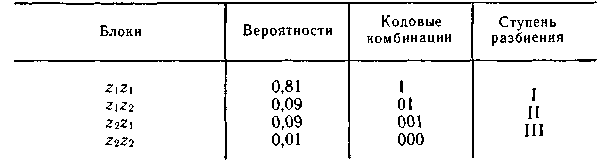
Так как знаки статистически не связаны, вероятности блоков определяются как произведение вероятностей составляющих знаков.

Среднее число символов на блок получается равным 1,29, а на букву — 0,645.

Кодирование блоков, содержащих по три знака, дает еще больший эффект. Соответствующий ансамбль и коды приведены в табл. 5.7.

Таблица 5.7

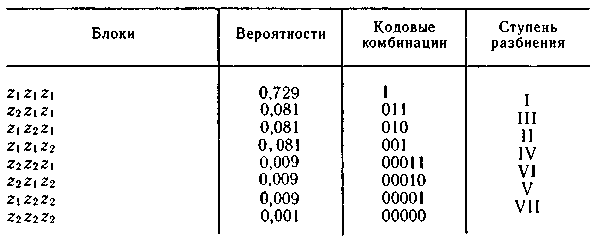
Среднее число символов на блок равно 1,59, а на знак — 0,53, что всего на 12 % больше энтропии. Теоретический минимум Η(Ζ) = 0,47 может быть достигнут при кодировании блоков, включающих бесконечное число знаков:

Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков не связано с учетом все более далеких статистических связей, так как нами рассматривались алфавиты с некоррелированными знаками. Повышение эффективности определяется лишь тем, что набор вероятностей, получающихся при укрупнении блоков, можно делить на более близкие по суммарным вероятностям подгруппы.

Рассмотренная методика Шеннона — Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы. Например, множество вероятностей, приведенных в табл. 5.5, можно было бы разбить так, как показано в табл. 5.8.

Таблица 5.8

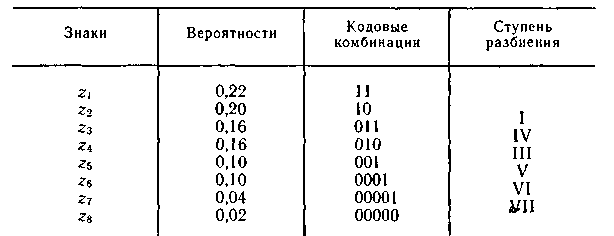
От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода методика сводится к следующему. Буквы алфавита сообщений выписывают в основной столбец в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Пример 5.8. Используя методику Хаффмана, осуществим эффективное кодирование ансамбля знаков, приведенного в табл. 5.5.

Процесс кодирования поясняется табл. 5.9. Для составления кодовой комбинации, соответствующей данному знаку, необходимо проследить путь перехода знака по строкам и столбцам таблицы.

Таблица 5.9

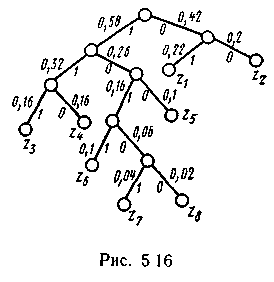Для наглядности строим кодовое дерево. Из точки, соответствующей вероятности 1, направляем две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до вероятности каждой буквы. Кодовое дерево для алфавита букв, рассматриваемого в табл. 5.9, приведено на рис. 5.16.

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:

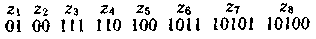
Требование префиксности эффективных кодов.Рассмотрев методики построения эффективных кодов, нетрудно убедиться в том, что эффект достигается благодаря присвоению более коротких кодовых комбинаций более вероятным знакам и более длинных менее вероятным знакам. Таким образом, эффект связан с различием в числе символов кодовых комбинаций. А это приводит к трудностям при декодировании. Конечно, для различения кодовых комбинаций можно ставить специальный разделительный символ, но при этом значительно снижается эффект, которого мы добивались, так как средняя длина кодовой комбинации по существу увеличивается на символ.

Более целесообразно обеспечить однозначное декодирование без введения дополнительных символов. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом более длинной комбинации. Коды, удовлетворяющие этому условию, называют префиксными кодами. Последовательность 100000110110110100 комбинаций префиксного кода, например кода

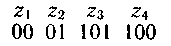
декодируется однозначно:

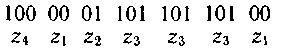
Последовательность 000101010101 комбинаций непрефиксного кода, например кода

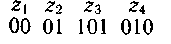
(комбинация 01 является началом комбинации 010), может быть декодирована по-разному:

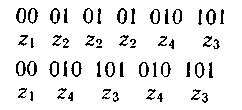
или

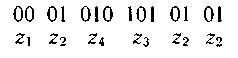
Нетрудно убедиться, что коды, получаемые в результате применения методики Шеннона — Фано или Хаффмена, являются префиксными.

Методы эффективного кодирования коррелированной последовательности знаков. Декорреляция исходной последовательности может быть осуществлена путем укрупнения алфавита знаков. Подлежащие передаче сообщения разбиваются на двух-, трех- или n-знаковые сочетания, вероятности которых известны:

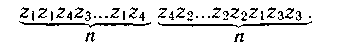
Каждому сочетанию ставится в соответствие кодовая комбинация по методике Шеннона — Фано или Хаффмена.

Недостаток такого метода заключается в том, что не учитываются корреляционные связи между знаками, входящими в состав следующих друг за другом сочетаний. Естественно, он проявляется тем меньше, чем больше знаков входит в каждое сочетание.

Указанный недостаток устраняется при кодировании по методу диаграмм, триграмм или l-грамм. Условимся называть l-граммой сочетание из l смежных знаков сообщения. Сочетание из двух смежных знаков называют диаграммой, из трех — триграммой и т. д.

Теперь в процессе кодирования l-грамма непрерывно перемещается по тексту cсообщения:

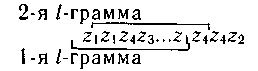
Кодовое обозначение каждого очередного знака зависит от l-1 предшествовавших ей знаков и определяется по вероятностям различных l-грамм на основании методики Шеннона - Фано или Хаффмена.

Конкретное значение l выбирают в зависимости от степени корреляционной связи между знаками или сложности технической реализации кодирующих и декодирующих устройств.

Недостатки системы эффективного кодирования. Причиной одного из недостатков является различие в длине кодовых комбинаций. Если моменты снятия информации с источника неуправляемы (например, при непрерывном съеме информации с запоминающего устройства на магнитной ленте), кодирующее устройство через равные промежутки времени выдает комбинации различной длины. Так как линия связи используется эффективно только в том случае, когда символы поступают в нее с постоянной скоростью, то на выходе кодирующего устройства должно быть предусмотрено буферное устройство («упругая» задержка). Оно запасает символы по мере поступления и выдает их в линию связи с постоянной скоростью. Аналогичное устройство необходимо и на приемной стороне.

Второй недостаток связан с возникновением задержки в передаче информации.

Наибольший эффект достигается при кодировании длинными блоками, а это приводит к необходимости накапливать знаки, прежде чем поставить им в соответствие определенную последовательность символов. При декодировании задержка возникает снова. Общее время задержки может быть велико, особенно при появлении блока, вероятность которого мала. Это следует учитывать при выборе длины кодируемого блока.

Еще один недостаток заключается в специфическом влиянии помех на достоверность приема. Одиночная ошибка может перевести передаваемую кодовую комбинацию в другую, не равную ей по длительности. Это повлечет за собой неправильное декодирование ряда последующих комбинаций, который называют треком ошибки.

Специальными методами построения эффективного кода трек ошибки стараются свести к минимуму [18].

Следует отметить относительную сложность технической реализации систем эффективного кодирования.

§ 5.5. ТЕХНИЧЕСКИЕ СРЕДСТВА КОДИРОВАНИЯ

И ДЕКОДИРОВАНИЯ ЭФФЕКТИВНЫХ КОДОВ

Из материала предыдущего параграфа следует, что в общем случае кодер источника должен содержать следующие блоки:

устройство декорреляции, ставящее в соответствие исходной последовательности знаков другую декоррелированную последовательность знаков;

собственно кодирующее устройство, ставящее в соответствие декоррелированной последовательности знаков последовательность кодовых комбинаций;

буферное устройство, выравнивающее плотность символов перед их поступлением в линию связи.

Декор источника соответственно должен содержать:

устройство декодирования последовательности кодовых комбинаций в последовательность знаков;

буферное устройство, выравнивающее интервалы между знаками;

устройство pекорреляции, осуществляющее операцию, обратную декорреляции.

В частном случае, когда корреляционные связи между знаками отсутствуют и имеется возможность управлять моментами считывания информации с источника, схемы кодера и декодера источника существенно упрощаются.

Ограничимся рассмотрением этого случая применительно к коду, приведенному в табл. 5.9.

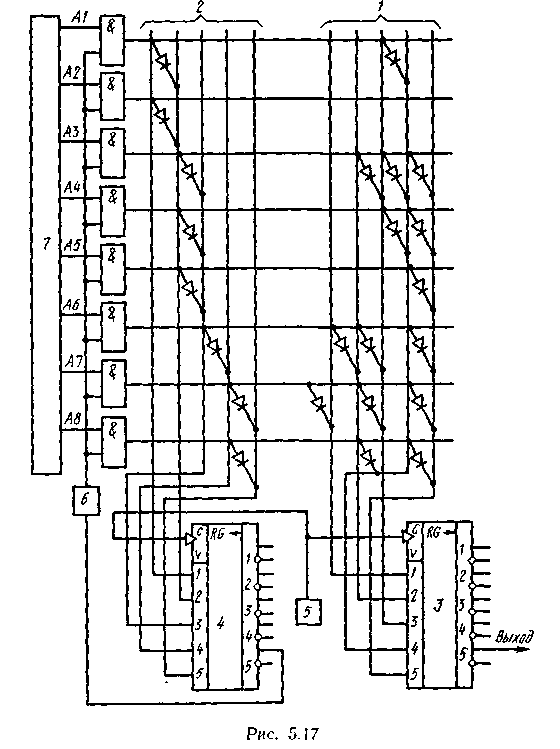Схема кодера источника приведена на рис. 5.17. В ней можно выделить основной матричный шифратор 1 с регистром 3 и вспомогательную схему управления считыванием информации, содержащую матричный шифратор 2 — с регистром сдвига 4. Число горизонтальных шин шифраторов равно числу кодируемых знаков, а число вертикальных шин в каждом из них равно числу символов в самой длинной комбинации используемого эффективного кода.

Включение диодов в узлах ί-й горизонтальной шины основного шифратора 1 обеспечивает запись в регистр сдвига 3 кодовой комбинации, соответствующей знаку z_i.

Во вспомогательном шифраторе 2 к каждой i-й горизонтальной шине подключен только один диод, обеспечивающий запись единицы в такую ячейку регистра 4, номер которой совпадает с числом символов в кодовой комбинации, соответствующей знаку z_i.

Кодирование очередного знака z_i, выдаваемого источником информации 7, осуществляется посредством подачи через элементы И импульса на ί-ю горизонтальную шину шифраторов от импульсного источника питания 6. При этом в регистр сдвига 3 записывается кодовая комбинация, соответствующая знаку z_i, а в регистр 4 — единица, несущая информацию о конце этой кодовой комбинации. Продвигающими импульсами генератора 5 записанная в регистре 3 кодовая комбинация символ за символом выводится в канал связи. Посредством того же генератора сдвигается и единица в регистре 4. Соответствующий ей импульс появится на выходе регистра в тот момент, когда из регистра 3 будет выведен последний символ кодовой комбинации. Этот импульс используется как управляющий для перехода к кодированию следующего знака.

На рис. 5.18 приведена схема декодирующего устройства, разработанного Гильбертом и Муром.

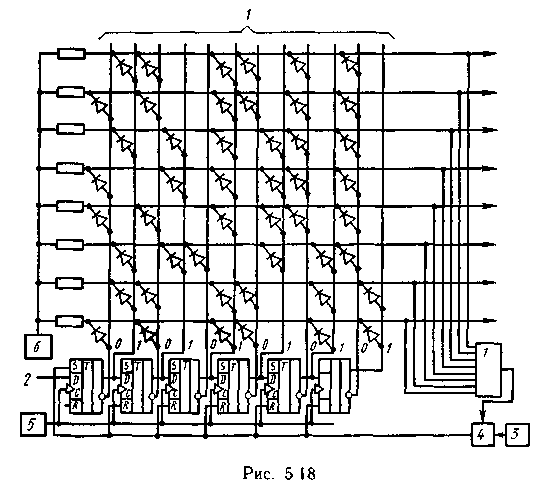Символы декодируемой кодовой комбинации, поступающие на вход 2, продвигаются по нему импульсами тактового генератора 5. Так как некоторые из поступающих кодовых комбинаций начинаются с одного или нескольких нулей, то непосредственно по содержанию регистра невозможно определить начало этих комбинаций, а следовательно, и правильно их декодировать.

Для однозначного определения начала каждой кодовой комбинации число ячеек регистра берут на единицу больше числа символов в самой длинной комбинации используемого эффективного кода. В дополнительной первой ячейке регистра перед поступлением в него очередной декодируемой комбинации всегда записывают единицу. Продвигаясь по регистру, она сигнализирует о начале кодовой комбинации, а следовательно, и о ее длине.

За каждым тактовым импульсом следует импульс с источника 6, питающего матричный дешифратор 1. Последний построен в соответствии с комбинациями используемого кода, в котором со стороны старшего разряда приписана лишняя единица. При поступлении в регистр последнего символа декодируемой первой кодовой комбинации очередной импульс от источника 6 приводит к появлению импульса напряжения на выходе i-й шине дешифратора, что соответствует приему знака z_i. Через схему ИЛИ этот импульс записывается в промежуточную ячейку памяти 4 и при считывании очередным импульсом с генератора сброса 3 используется для установления всех ячеек регистра в исходное состояние (в первой ячейке 1, в остальных 0). Далее поступает следующая кодовая комбинация и процесс декодирования повторяется.

Контрольные вопросы

1. В чем преимущества использования двоичных кодов при передаче, хранении и обработке информации?

2. С какой целью применяется код Грея?

3. В чем сущность метода поразрядного уравновешивания?

4. Сравните различные типы аналого-цифровых преобразователей по быстродействию и точности.

5. Что понимают под криптографическим закрытием информации?

6. Какие требования предъявляются к современным методам криптографического закрытия информации?

7. Назовите основной недостаток шифрования гаммированием.

8. В чем суть эффективного статистического кодирования?

9. Сформулируйте и поясните основную теорему Шеннона о кодировании для канала без помех.

10. Каковы причины эффективности кодирования длинных последовательных знаков?

11. За счет чего при эффективном кодировании уменьшается средняя длина кодовой комбинации?

12. До какого предела может быть уменьшена средняя длина кодовой комбинации при эффективном кодировании?

13. В чем преимущество методики построения эффективного кода, предложенной Хаффманом, по сравнению с методикой Шеннона — Фано?

14. Какому основному условию должны удовлетворить эффективные коды?

15. Перечислите сложности, возникающие при использовании эффективных кодов.

ГЛАВА 6. КОДИРОВАНИЕ ИНФОРМАЦИИ ПРИ ПЕРЕДАЧЕ

ПО ДИСКРЕТНОМУ КАНАЛУ С ПОМЕХАМИ

§ 6.1. ОСНОВНАЯ ТЕОРЕМА ШЕННОНА О КОДИРОВАНИИ

ДЛЯ КАНАЛА С ПОМЕХАМИ

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных им в виде теоремы:

1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.

2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.

Хотя доказательство этой теоремы, предложенной Шенноном, в дальнейшем подвергалось более глубокому и строгому математическому представлению [34], идея его осталась неизменной. Доказывается только существование искомого способа кодирования, для чего находят среднюю вероятность ошибки по всем возможным способам кодирования и показывают, что она может быть сделана сколь угодно малой. При этом существует хотя бы один способ кодирования, для которого вероятность ошибки меньше средней.

Доказательство теоремы. Будем кодировать сообщения такой длительности Т, чтобы была справедлива теорема об асимптотической вероятности длинных последовательностей букв (см. § 4.2). Тогда при заданной производительности источника сообщений Ī(Ζ) кодированию подлежат только Ν(z) типичных последовательностей, причем:

Ориентируясь на равновероятное поступление в канал любого из m различных элементарных входных сигналов и отсутствие между ними статистической связи на входе канала, можно сформировать N(u) равновероятных последовательностей длительности Т, причем