Влияние способов закрепления концов стержня
На рис. 8.3 показаны формы потери устойчивости стержней длиной 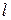 с различными случаями закрепления концов. Случай б) нами рассмотрен при выводе формулы Эйлера. Этот случай называют основным случаем закрепления.
с различными случаями закрепления концов. Случай б) нами рассмотрен при выводе формулы Эйлера. Этот случай называют основным случаем закрепления.
Для других случаев закрепления можно повторить все выкладки, изменяя в каждом случае только граничные условия и получить соответствующие значения 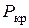 . Однако можно пойти другим путем.
. Однако можно пойти другим путем.
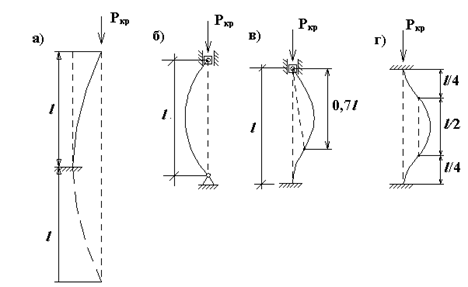
Рис.8.3
Сравнивая рис. а) и б) видим, что изогнутая ось стержня, защемленного одним концом, находится в тех же условиях, что и верхняя часть стержня длиной 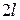 с шарнирными концами. Следовательно,
с шарнирными концами. Следовательно, 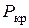 для стойки длиной
для стойки длиной 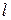 с одним защемленным концом будет та же, что для стойки длиной
с одним защемленным концом будет та же, что для стойки длиной 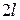 с шарнирными концами. Поэтому, подставляя
с шарнирными концами. Поэтому, подставляя 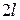 вместо
вместо 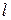 в формулу Эйлера найдем:
в формулу Эйлера найдем:
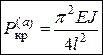 – Эйлерова сила для стержня с
– Эйлерова сила для стержня с
одним защемленным концом.
На рис. г) показана потеря устойчивости стержня с двумя защемленными концами. Видно, что она симметрична относительно середины стержня; точки перегиба изогнутой оси (в которых, как известно, изгибающие моменты равны нулю) расположены на четвертях длины стержня. Следовательно, здесь средняя часть стержня длиной 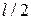 находится в тех же условиях, что и шарнирно закрепленный по концам стержень. Поэтому, подставляя здесь
находится в тех же условиях, что и шарнирно закрепленный по концам стержень. Поэтому, подставляя здесь 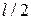 вместо
вместо 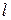 в формулу Эйлера найдем
в формулу Эйлера найдем
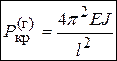 –Эйлерова сила для стержня с двумя
–Эйлерова сила для стержня с двумя
защемленными концами
Полученные формулы Эйлера при различных закреплениях концов стержня можно записать в общем виде:
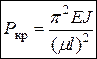 (8.7)
(8.7)
Здесь 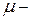 коэффициент приведения длины.
коэффициент приведения длины.
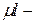 приведенная длина стержня.
приведенная длина стержня.
Для основных случаев закрепления стержней, показанных на рис. 8.3 коэффициент 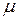 имеет следующие значения:
имеет следующие значения:
а) один конец защемлен, другой свободный  ;
;
б) с шарнирными концами 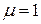 ;
;
в) один конец защемлен, другой шарнирный 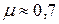 ;
;
г) с двумя заделанными концами 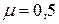 .
.
Зная критическую силу, можно найти критическое напряжение, поделив силу на площадь. Так как на деформации стержня местные ослабления площади сечения (отверстиями) сказываются мало, то при расчетах на устойчивость принято использовать полную площадь сечения. Следовательно, в формуле Эйлера 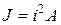 . Тогда
. Тогда
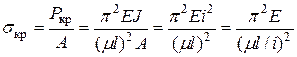
Окончательно
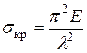 (8.8)
(8.8)
Здесь
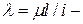 гибкость стержня. (8.9)
гибкость стержня. (8.9)
Гибкость стержня важная характеристика стержней при расчетах их на устойчивость. В (8.9) надо подставлять 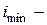 минимальный радиус инерции сечения, поэтому
минимальный радиус инерции сечения, поэтому 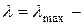 максимальная гибкость. Стержень теряет устойчивость в той плоскости, в которой его гибкость максимальная.
максимальная гибкость. Стержень теряет устойчивость в той плоскости, в которой его гибкость максимальная.
В неочевидных случаях надо вычислить отдельно: 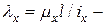 гибкость относительно (вокруг) оси
гибкость относительно (вокруг) оси 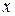 и
и 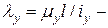 гибкость относительно оси
гибкость относительно оси 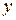 , т.е. в плоскости
, т.е. в плоскости 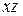 . Если
. Если 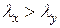 , то
, то 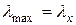 и расчет на продольный изгиб надо вести в плоскости изгиба
и расчет на продольный изгиб надо вести в плоскости изгиба 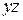 , а если
, а если 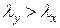 , то
, то 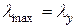 и расчет вести в плоскости
и расчет вести в плоскости 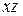 . Это очень важно, т.к. в случае ошибки расчет ведут в одной плоскости, а стержень теряет устойчивость в другой плоскости.
. Это очень важно, т.к. в случае ошибки расчет ведут в одной плоскости, а стержень теряет устойчивость в другой плоскости.
Для цилиндрического шарнира (вдоль оси 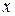 ) относительно оси
) относительно оси 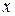 считается шарнир, а относительно оси
считается шарнир, а относительно оси 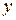 можно принять защемление. Однако, следует иметь ввиду, что на практике редко удается осуществить защемление. Достаточно возможности небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях близких к шарнирному опиранию. Поэтому обычно принимают
можно принять защемление. Однако, следует иметь ввиду, что на практике редко удается осуществить защемление. Достаточно возможности небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях близких к шарнирному опиранию. Поэтому обычно принимают 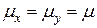 .
.
Формула (8.8) тоже формула Эйлера для критических напряжений.
Пределы применимости формулы Эйлера. Потеря устойчивости за пределами пропорциональности
Формула Эйлера получена из интегрирования дифференциального уравнения упругой оси балки, т.е. предполагалось, что стержень работает в пределах упругих деформаций по закону Гука. Недаром в формуле Эйлера фигурирует модуль Юнга Е.
Следовательно, формулой Эйлера нельзя пользоваться для оценки устойчивости стержней, если критические напряжения, вычисленные по ней, получаются выше предела пропорциональности (где закон Гука не применим).
Итак, формула Эйлера применима при соблюдении условия
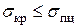 или
или 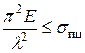 , откуда
, откуда
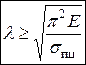
Здесь правая часть представляет наименьшее (предельное) значение гибкости стержня, при котором можно пользоваться формулой Эйлера и обозначается
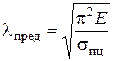 (8.10)
(8.10)
Условие применимости формулы Эйлера тогда примет вид:
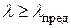 (8.11)
(8.11)
Для Ст.3 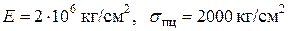 и
и 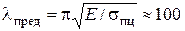 .
.
Для Ст.5 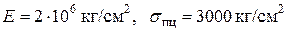 и
и 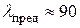 .
.
Для чугуна 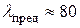 .
.
Для дерева 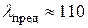 .
.
При гибкости стержня, меньше предельной, критическое напряжение, определенное по формуле Эйлера, получается значительно выше 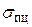 .
.
Например, при 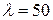 (Ст.3)
(Ст.3) 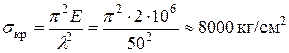 , т.е. величина
, т.е. величина 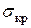 оказывается значительно больше предела прочности.
оказывается значительно больше предела прочности.
Ошибочное использование формулы Эйлера для вычисления 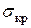 и проверки устойчивости при малых гибкостях, приводили иногда к серьезным катастрофам сооружений. Итак, решение Эйлера применимо на практике лишь для тонких и длинных стержней с большой гибкостью. Между тем на практике часто встречаются стержни с малой гибкостью.
и проверки устойчивости при малых гибкостях, приводили иногда к серьезным катастрофам сооружений. Итак, решение Эйлера применимо на практике лишь для тонких и длинных стержней с большой гибкостью. Между тем на практике часто встречаются стержни с малой гибкостью.
Опыты показали, что если по Эйлеру 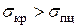 , то действительные критические напряжения значительно ниже определенных по Эйлеру.
, то действительные критические напряжения значительно ниже определенных по Эйлеру.
Важнейшим источником для установления действительных критических напряжений за пределом пропорциональности, т.е. при малых и средних гибкостях, явились результаты эксперимента.
Стержни, для расчета на устойчивость которых нельзя пользоваться формулой Эйлера, можно разбить на две большие группы:
1) Стержни с малой гибкостью
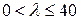
Для таких стержней нельзя говорить о явлении потери устойчивости прямолинейной формы стержня в том смысле, как это имеет место для тонких и длинных стержней. Эти короткие стержни будут выходить из строя главным образом от потери прочности, т.е. напряжения сжатия в них достигнут 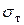 (для пластичных) или
(для пластичных) или 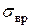 (для хрупких) материалов.
(для хрупких) материалов.
Поэтому для коротких толстых стержней 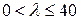 , за критические напряжения принимают:
, за критические напряжения принимают:
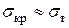 или
или 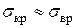 (8.12)
(8.12)
2) Стержни средней гибкости
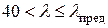
Для конструкционной Ст.3 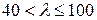 . С подобными значениями гибкости инженер чаще всего встречается на практике.
. С подобными значениями гибкости инженер чаще всего встречается на практике.
Эти стержни при сжатии теряют свою прямолинейную форму и разрушаются от продольного изгиба. В опытах для них можно отметить наличие ясно выраженной критической силы в Эйлеровом смысле. Для таких стержней критические напряжения получаются выше предела пропорциональности и ниже предела текучести материалов.
На основании обширного опытного материала, собранного профессором Ф. Ясинским, им была предложена эмпирическая формула для определения критических напряжений подобных стержней
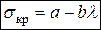 – формула Ясинского (8.13)
– формула Ясинского (8.13)
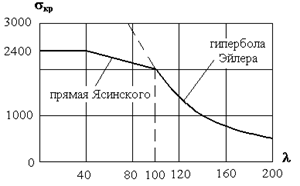 Рис.8.4
Рис.8.4
| Здесь 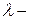 максимальная гибкость стержня, а и максимальная гибкость стержня, а и 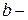 постоянные, зависящие от материала, приводятся в справочниках.
Например:
Для Ст.3 постоянные, зависящие от материала, приводятся в справочниках.
Например:
Для Ст.3 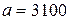 кг/см2, кг/см2, 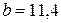 кг/см2.
Для дерева кг/см2.
Для дерева 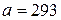 кг/см2, кг/см2, 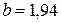 кг/см2. кг/см2.
|
На основании всего вышесказанного можно построить график критических напряжений (в зависимости от гибкости) для любого материала.
Для конструкционной Ст.3 с 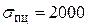 кг/см2 и
кг/см2 и 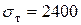 кг/см2 этот график (диаграмма) имеет вид, показанной на рис. 8.4. На этом графике четко выделяется три зоны:
кг/см2 этот график (диаграмма) имеет вид, показанной на рис. 8.4. На этом графике четко выделяется три зоны:
1) 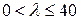
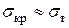
2) 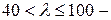 прямая Ясинского
прямая Ясинского
3) 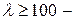 гипербола Эйлера
гипербола Эйлера
Пунктиром показана гипербола Эйлера за 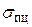 , которой нельзя пользоваться при
, которой нельзя пользоваться при 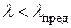 .
.
Расчет стержней на устойчивость.
Коэффициент уменьшения основного допускаемого напряжения
Для сжатых стержней кроме условия прочности
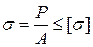 , где
, где 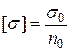 (А)
(А)
должно быть удовлетворено одновременно условие устойчивости
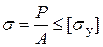 (В)
(В)
где 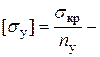 допустимые напряжения на устойчивость,
допустимые напряжения на устойчивость, 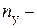 коэффициент запаса устойчивости.
коэффициент запаса устойчивости.
Обычно 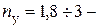 имеет более высокое значение, чем коэффициент
имеет более высокое значение, чем коэффициент 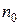 запаса прочности.
запаса прочности.
Зависимости (А) и (В) удобны для проверки прочности и устойчивости уже спроектированных стержней.
Для удобства проектировочных расчетов введено понятие коэффициент уменьшения основного допускаемого напряжения, который обозначается буквой 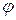 .
.
Найдем отношение 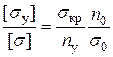 или
или 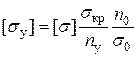
Обозначим 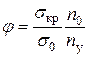 (С)
(С)
Получим 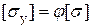 (8.14)
(8.14)
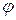 еще называют коэффициентом продольного изгиба в Строительных Нормах. Для ряда значений гибкости
еще называют коэффициентом продольного изгиба в Строительных Нормах. Для ряда значений гибкости 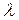 , по вышеприведенным формулам или графикам (рис. 8.4) можно найти величины
, по вышеприведенным формулам или графикам (рис. 8.4) можно найти величины 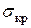 . Далее, зная
. Далее, зная 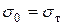 или
или 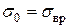 и выбрав коэффициенты
и выбрав коэффициенты 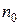 и
и 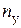 , по зависимости (С) можно составить для данного материала таблицы значений коэффициента
, по зависимости (С) можно составить для данного материала таблицы значений коэффициента 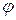 в функции от гибкости
в функции от гибкости 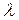 , т.е.
, т.е. 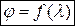 .
.
Такие таблицы приводятся в учебниках и задачниках по сопротивлению материалов. Пользуясь этими таблицами удобно подбирать сечения сжатых стержней. 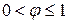
Дата добавления: 2016-10-18; просмотров: 4449;











