Параметры цифровых микросхем различных серий («логик»)
В настоящее время практически все цифровые элементы, а также их комбинации выпускаются в виде интегральных микросхем. При этом основные параметры цифровых элементов, изготовленных по разным технологиям (за рубежом употребляют понятие «разные логики») существенно различаются. В настоящее время наиболее распространены три технологии: транзисторно-транзисторная (ТТЛ, в зарубежной версии ТТL), комплементарная металл-окисел-полупроводниковая (КМОП или СМОS), а также эмиттерно-связанная (ЭСЛ). В некоторых учебных изданиях, в частности – китайских, цифровые микросхемы с ЭСЛ-логикой не упоминаются; возможно, это происходит из-за того, что схемы этого типа по многим параметрам уступают микросхемам с ТТЛ и КМОП логиками. Ниже приведена сводная таблица основных эксплуатационных параметров цифровых схем (табл. 11.4). Следует иметь ввиду, что в таблице приведены усредненные параметры по микросхемам различного назначения, а параметр «потребляемая мощность» усреднен еще и по режимам работы (с различным токопотреблением).
Табл. 11.4
| Параметр | Тип логики | ||
| ТТЛ | ЭСЛ | КМОП | |
| Напряжение питания Е, В | + 5 | − 5,2 | + 3…5 |
| Уровень U1, В | + 2,4 | − 0,9 | ≈Е |
| Уровень U0, В | + 0,4 | − 0,6 | ≈0 |
| Быстродействие (время переключения), нс | 2,9 | ||
| Потребляемая мощность, мВт | 0,1 | ||
| Коэффициент разветвления |
Как видно из таблицы, по большинству параметров наиболее предпочтительны микросхемы на базе КМОП-логики: это объясняется тем, что внутри микросхем этого типа располагаются полевые транзисторы, обладающие огромным входным сопротивлением по затвору (см. п. 2.7). Однако КМОП-элементы уступают по быстродействию. По этому важнейшему параметру наилучшими являются ЭСЛ-микросхемы, что вообще оправдывает их существование – все остальные параметры у этого типа схем плохие. Следует обратить внимание на полярность уровней логического нуля и логической единицы у ЭСЛ-схем. ТТЛ-схемы имеют средние значения параметров и именно этим объясняется их наибольшее распространение. Применяя этот тип микросхем, разработчики сложных цифровых электронных устройств находят компромисс при оптимизации эксплуатационных характеристик.
Двоичный счетчик
Триггеры – схемы, которые с точки зрения «булевой» алгебры, фиксируют значение всего одного разряда двоичного числа. Необходимость такого «счета до двух» возникает весьма редко. Поэтому для фиксации многоразрядных двоичных чисел применяют более сложные схемы, являющиеся комбинациями нескольких триггеров – двоичные счетчики.
Схема трехразрядного двоичного счетчика прямого счета приведена на рис.11.13. Как видно, счетчик представляет собой последовательное («каскадное») соединение Т-триггеров. Количество этих триггеров равно разрядности двоичного числа.
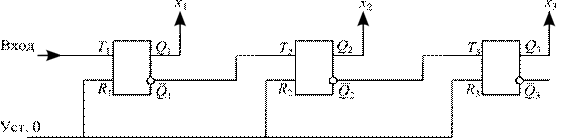
|
| Рис.11.13 |
Принцип действия счетчика поясняют диаграммы напряжение в точках схемы, приведенные на рис.11.14. Из рисунка видно, как десятичные номера импульсов, поступающих на вход схемы превращаются в эквивалентные двоичные числа, записанные в параллельном коде (параллельным называется представление многоразрядного числа, при котором каждому разряду числа соответствует своя «шина», т. е. провод).
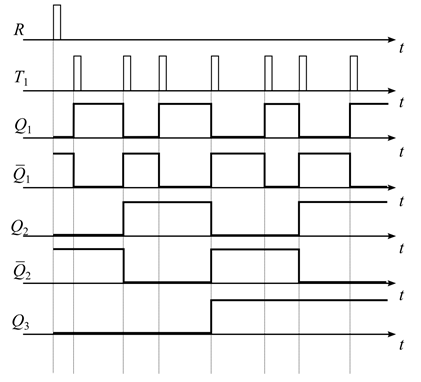
|
| Рис.11.14 |
Перед началом счета все триггера необходимо обнулить, подав на счетчик прежде всего импульс «установка нуля» (уст.0) на R-входы. Следует обратить внимание на соединение триггеров: на Т-вход следующего триггера поступает переключающий сигнал с инверсного ( 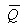 ) выхода предыдущего. Такое соединение применено с учетом схемотехнических решений во входных цепях триггеров (см. п. 11.4).
) выхода предыдущего. Такое соединение применено с учетом схемотехнических решений во входных цепях триггеров (см. п. 11.4).
Чаще всего переключается триггер, непосредственно получающий сигналы с генератора импульсов. Именно на его Главном выходе формируется младший разряд двоичного числа. Старший разряд формируется на шине, соединенной с Q-выходом максимально удаленного от входа триггера.
Если не предпринять дополнительных мер, то счетчик досчитает до седьмого импульса, при этом на выходах триггеров будет сформирован код 111 – и далее восьмым импульсом обнулится, а затем возобновит счет. При необходимости остановить счет по заданному номеру импульса схему счетчика надо дополнить (рис.11.15.) – главные и инверсные выходы триггеров соединить со схемой И так, чтобы при достижении нужной комбинации на ее выходе образовалась бы логическая единица, которая обнулит все триггеры. После этого счет импульсов возобновится, но уже не с восьмого импульса.
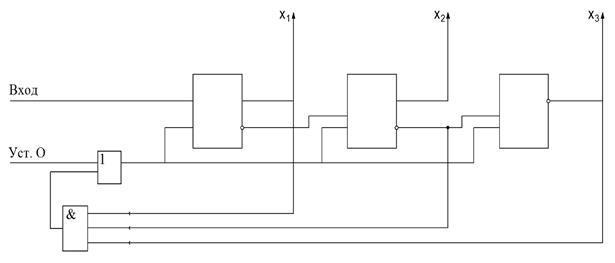
|
| Рис.11.15 |
Регистр
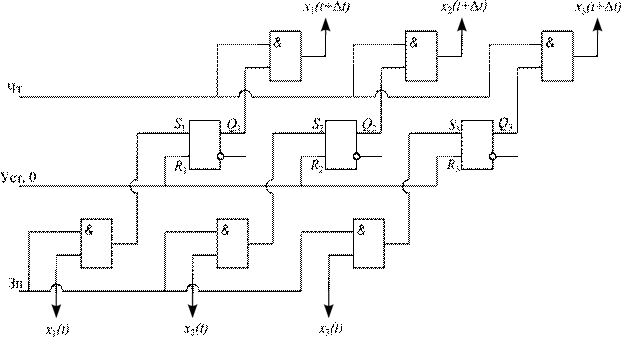
Регистром называют схему хранения многоразрядных двоичных чисел, своего рода цифровую линию задержки. Второе распространенное название регистра – ОЗУ (оперативное запоминающее устройство). Изображенный на рис. 11.16. регистр рассчитан на хранение трехразрядных двоичных чисел в течение одного «шага» (существуют более сложные схемы, которые хранят двоичные числа в течение десятков шагов, а извлечение чисел из регистра может идти как в прямой, так и в обратной последовательности).
|
| Рис. 11.16 |
Главными элементами хранения являются RS-триггеры. Перед записью в регистр нового двоичного числа необходимо обнулить все триггеры, используя для этого сигнал (уст.0), подаваемый на все R-входыодновременно. Затем, синхронно во всех разрядах, в триггеры записывают многоразрядное двоичное число. В целях синхронизации записи (команда Зп) сигналы на входы триггеров подают не непосредственно, а через «линейку» схем И. Чтение чисел (команда Чт)такжеобеспечивает синхронную передачу многоразрядного двоичного числа на выход, потребителю – для этой цели предусмотрена вторая «линейка» схем И. Чтение является неразрушающим и одно и то же число может быть считано неоднократно, с разными задержками относительно записи.
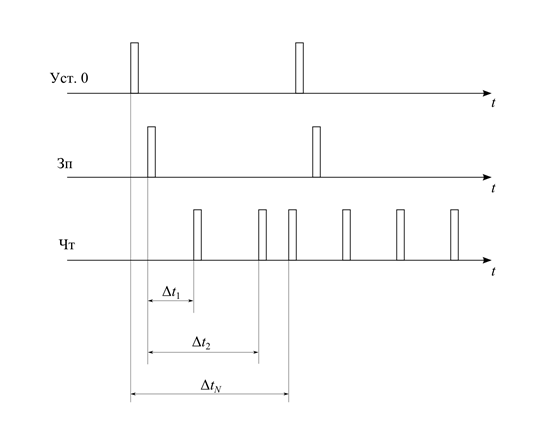
Следует отметить, что регистр как цифровая линия задержки существенно превосходит по своим возможностям аналоговые ЛЗ, так как обеспечивает практически неограниченное время задержки. Однако при этом аналоговую величину первоначально требуется преобразовать в цифровой формат. Порядок работы регистра поясняют диаграммы на рис. 11.17.
11.10. Мультиплексор и демультиплексор, кóдер
Выше во всех рассмотренных примерах двухуровневый сигнал был представлен в параллельном коде. Другое возможное представление - последовательный код, при использовании которого уровни напряжения, соответствующие различным разрядам двоичного числа, передаются поочередно.
|
| Рис. 11.17 |
Очевидно, что любое представление имеет свои положительные и отрицательные стороны: передача значений всех разрядов одновременно происходит значительно быстрее, чем поочередная, поэтому быстродействие электронных устройств при использовании параллельных кодов выше, чем при использовании последовательных. Однако при параллельном кодировании каждому разряду требуются своя шина (провод), гнездо на разъеме, а при передаче с использованием радиоволн – своя частота, в то время как последовательный код можно передать по одной шине.
Таким образом, для оптимизации электронных устройств бывает необходимо преобразовать параллельный код в последовательный и наоборот.
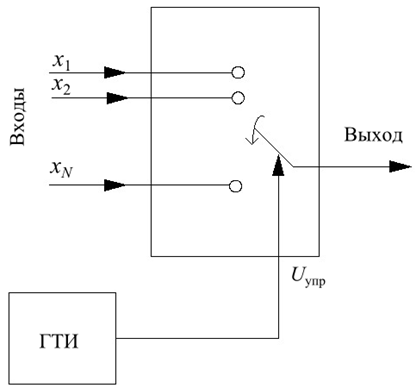
Схему, преобразующую параллельный код в последовательный, называют мультиплексором. Ее принцип действия поясняет рис. 11.18. Схема имеет много входов – по количеству разрядов двоичного числа и один выход. Входы поочередно соединяются с выходом с помощью блока схем И (или электронных ключей). Управление коммутацией схем И осуществляется от тактового генератора (высокостабильного генератора прямоугольных импульсов) через счетчик.
|
| Рис. 11.18 |
Примерно так же работает схема, выполняющая обратную функцию – преобразование последовательного кода в параллельный. Ее называют демультиплексором. Схема имеет один вход и много выходов – по одному для каждого разряда двоичного числа в параллельном коде. Вход поочередно соединяются с выходами с помощью блока схем И. Управление коммутацией схем И осуществляется от тактового генератора через счетчик.
При использовании преобразования параллельного кода в последовательный и обратно следует помнить, что конечное быстродействие определяет наименее быстрое звено электронной системы – участок, на котором двухуровневый сигнал передается последовательным кодом.
Преобразования кода, которые выполняют мультиплексор и демультиплексор – далеко не единственные. При этом состав и расположение нулей и единиц в коде при переходе из параллельной формы в последовательную не изменяется. Однако иногда возникает потребность в более существенном преобразовании кода. Дело в том, что в технике находят применяются коды, не соответствующие «булевой» алгебре – например, код Грэя. Код Грэя для первого разряда десятичных чисел приведен в табл. 11.5. Он обладает замечательным свойством – при увеличении десятичного числа на единицу в коде Грэя изменяется всегда только один символ, что делает вероятную погрешность преобразования независящей от значения числа. Однако для того, чтобы осуществить компьютерную обработку данных от датчика, вырабатываемых в форме кода Грэя, надо перевести их в код, соответствующий «булевой» алгебре. Эту операцию выполняет схема, которую называют «преобразователь код/код», или более коротко – кóдер.
Табл. 11.5
| Десятичное число | Код Грэя десятичного числа |
Дата добавления: 2016-10-07; просмотров: 2017;











