Проектирование участков графическим способом и его точность
При проектированииучастка графическим способом иногда поступают следующим способом: предварительно на глаз проектируют участок; вычисляют его площадь; затем проектируют недостающую или избыточную площадь к заданной, при этом предварительно спроектированную площадь определяют планиметром или вычисляют аналитическим способом. Недостающую или избыточную площадь проектируют в форме треугольника или трапеции,с учетом требований к направлениюпроектной линии.
Проектирование треугольником выполняют в случае, когда проектная линия должна проходить через определенную точку, при этом по заданной площади и известной высоте (или основанию) определяют основание (или высоту) треугольника.
На рисунке 7.1,а, изображена часть землепользования, в которой надо спроектировать площадь Р линией МN, проходящей через точку F.
Пусть разность между проектной площадью Ри площадью четырехугольника ВСDF равна Р1. Если проектом установлено, что северный конец проектной линии должен пройти через точкуF, то южный конец ее пересечет линию АВ вправо от точки В. От этой точки расположится основание а треугольника ВFК, форму которого имеет недостающая площадь Р1. Высотой треугольника явится перпендикуляр h, опущенный из точки Fна линию АВ или на ее продолжение (рис. 7.1,6). Длину его определяют по плану графически. Тогда основание треугольника
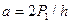 . (7.1)
. (7.1)
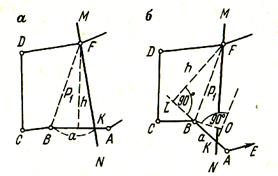
Рисунок 7.1 – Проектирование площади линией, проходящей через заданную точку
Полученное расстояние а выписывают на проектный план и схематической чертеж. Его используют при перенесении проекта в натуру для получения на местности проектной точки К.
Если вычисленный отрезок а длиннее линии АВ, т. е. площадь Р1 больше площади треугольника АВF, то вычисляют площадь этого треугольника и находят пересечение проектной линии с линией АЕ предыдущим способом. Для этого измеряют высоту от точки F до линии АЕ или до ее продолжения.
Для определения точности вычисления расстояния а применим формулу
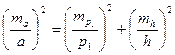 . (7.2)
. (7.2)
Если Р1 - заданная площадь, то ее можно считать безошибочной, т е. Р1 = 0, тогда
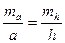 (7.3)
(7.3)
Следовательно, с какой относительной погрешностью измерена высота, с такой же относительной погрешностью будет вычислено основание и наоборот.
Проектирование трапецией производят, если проектная должна проходить параллельно заданному направлению. В случае по заданной площади и длине средней линии этой трапеции определенной по плану, вычисляют высоту трапеции, а потом ее боковые стороны. Проектирование трапецией менее точно, чем треугольником, из-за неточного измерения средней линии, так как положение ее неизвестно, если неизвестна высота.
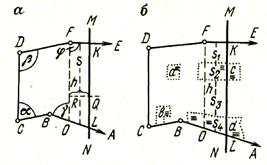
На рисунке 7.2,а изображена часть землепользования, в которой надо спроектировать площадь Р линией МN, параллельной линии DC. Для этого из точки F проводят линию FО, параллельную DC и вычисляют площадь ОВСDF.
|
Рисунок 7.2 – Проектирование участка в форме трапеции
Разность между проектной площадью Р и площадью ОВСDF равна P1 и представляет площадь трапеции, которую надо допроектировать .
Для этого предварительно определяют длину средней линии по плану, выбрав положение ее на глаз в соответствии с площадью P1, и вычисляют предварительное значение высоты по формуле
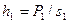 . (7.4)
. (7.4)
Отложив половину величины h1 от линии FО и проведя через полученную точку R линию, параллельную линии FО или DС, измеряют второе приближенное значение средней линии трапеции s2. Разделив Р1 на s2, получают второе, более точное значение высоты трапеции h2, которое может считаться окончательным, если расхождение его с h1 не превышает величины утроенной графической точности, деленной на отношение средней линии к высоте, т. е.
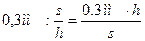 , (7.5)
, (7.5)
в противном случае получают новое (третье) значение средней линии и затем третье значение высоты. Расхождение окончательной длины средней линии с предыдущим ее значением не допускают более только что установленного предела. Получив окончательное значение высоты, откладывают его на перпендикуляре к линии FО и через полученную точку О проводят линию МN, параллельную DС.
Погрешность определения высоты h в зависимости от погрешностей площади Р1 и средней линии трапеции s может быть определена по формуле
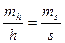 ,
,
т. е. относительная погрешность искомой высоты при этом способе равна относительной погрешности измерения средней линии. Чем меньше высота трапеции по сравнению со средней линией, чем меньше угол, образуемый боковыми сторонами трапеции FK и OL,
тем быстрее и точнее получается значение высоты.
Из рассмотренных выше примеров проектирования треугольником и трапецией видно, что проектирование треугольником точнее, так как необходимые данные для перенесения проекта в натуру получаются в результате вычислений, в то время как при проектировании трапецией отрезки FК. и ВL надо определять по плану с общей догрешностью, в которую, помимо погрешностей вычисления высоты h входят погрешности: откладывания высоты (0,08 мм); проведения проектной линии МN (0,08 мм) и графического определения промеров FК и ВL. Чтобы избежать накопления такого большого количества погрешностей, промер РК следует вычислить по формуле
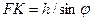 , (7.6)
, (7.6)
в которой угол φ получают как разность дирекционных углов линий DC и FЕ.
Отрезок ВL вычисляют по формуле
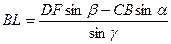 ,
,
в которой γ разность дирекционных углов линий ВА и СD.
При отсутствии геодезических данных по границе АВСDFE углы φ и γ можно измерить транспортиром, а отрезок ВL вычислить по формуле 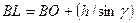 , в которой отрезок ВО определяют по плану графически. При этом в погрешность определения отрезка ВО войдет не только погрешность его графического определения (0,08 мм), но и погрешность нанесения точки В на план.
, в которой отрезок ВО определяют по плану графически. При этом в погрешность определения отрезка ВО войдет не только погрешность его графического определения (0,08 мм), но и погрешность нанесения точки В на план.
Точность проектирования участков в форме прямоугольника, параллелограмма и трапеции графическим способом можно вычислить по формуле
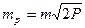 .
.
Дата добавления: 2021-01-11; просмотров: 604;











