Теория метода и описание установки
Момент инерции тел сложной формы определяется опытным путем. В данной работе для определения момента инерции тел используется метод крутильных колебаний маятника на трифилярном подвесе, период которого зависит от момента инерции колеблющегося тела.
Маятник на трифилярном подвесе состоит из платформы массой mn и радиусом R (рисунок 3.9), подвешенной на трех металлических нитях, прикрепленных к диску радиусом r<R и расположенных симметрично относительно оси системы ОО/ (ось ОО/ перпендикулярна диску и платформе).
При повороте диска на небольшой угол φ0 вокруг оси центр массы системы несколько приподнимается вдоль оси вращения и нижняя платформа начинает совершать крутильные колебания, период которых зависит от момента инерции системы. Резкий поворот верхнего диска на малый угол φ0<50 почти полностью исключает некрутильные колебания платформы (при колебании платформы верхний диск должен быть неподвижным).
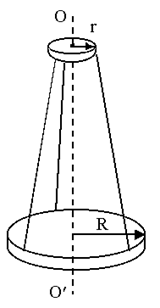
Рисунок 3.9
За четверть периода колебаний платформа поднимется на высоту 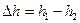 , и ее потенциальная энергия изменится на величину (рисунок 3.10)
, и ее потенциальная энергия изменится на величину (рисунок 3.10)
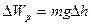 (3.18)
(3.18)
 В следующие четверть периода потенциальная энергия платформы переходит в кинетическую энергию, которая при начальной угловой скорости , равной нулю, запишется так:
В следующие четверть периода потенциальная энергия платформы переходит в кинетическую энергию, которая при начальной угловой скорости , равной нулю, запишется так:
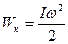 , (3.19)
, (3.19)
где ω – угловая скорость гармонического колебательного движения.
Затем кинетическая энергия переходит в потенциальную и т.д. По закону сохранения и превращения энергии (без учета сил трения) имеем:
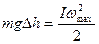 , (3.20)
, (3.20)
где ωmax – максимальная угловая скорость в момент прохождения положения равновесия.
Из этого выражения можно найти момент инерции системы
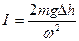 (3.21)
(3.21)
Платформа совершает гармонические крутильные колебания, поэтому угловое смещение φ платформы имеет следующую зависимость от времени:
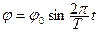 , (3.22)
, (3.22)
где φ0 – угловая амплитуда крутильных колебаний;
T – период полного колебания.
Угловую скорость платформы можно найти, взяв производную по времени от φ :
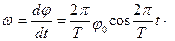 (3.23)
(3.23)
Она максимальна при 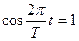 и равна
и равна

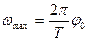 (3.24)
(3.24)
Вычислим величину 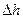 при повороте платформы на угол
при повороте платформы на угол 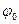 .
.
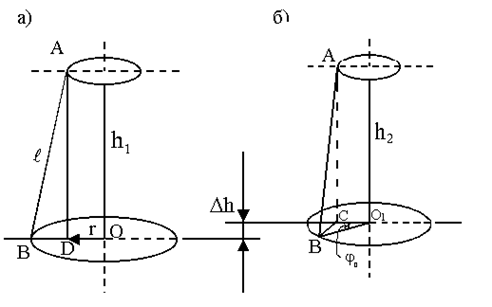
а – положение равновесия маятника;
б – положение максимального смещения маятника.
Рисунок 3.10
Из рисунка 3.10 видно, что
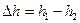 , или
, или
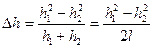 , (3.25)
, (3.25)
так как 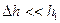 , то
, то 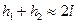
(l – длина нити).
h1 и h2 находим из треугольников ABD и ABC:
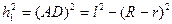 из Δ ABD
из Δ ABD
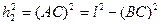 из Δ ABС.
из Δ ABС.
(BC) определяем из треугольника BCO как сторону, лежащую против угла 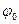 :
:
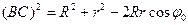 .
.
Тогда 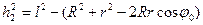 .
.
Подставляем значения 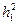 и
и 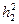 в формулу (3.25), получаем:
в формулу (3.25), получаем:
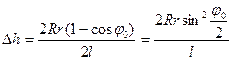 .
.
Так как угол 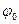 мал, то
мал, то 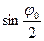 можно заменить аргументом
можно заменить аргументом 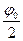 – в радианах:
– в радианах:
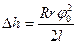 . (3.26)
. (3.26)
Подставляя 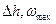 в формулу (3.20), окончательно получаем выражение для расчета момента инерции ненагруженной платформы:
в формулу (3.20), окончательно получаем выражение для расчета момента инерции ненагруженной платформы:
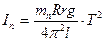 = mnК Т2, (3.27)
= mnК Т2, (3.27)
где mn – масса платформы;
К = 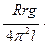 ,
,
R – радиус платформы;
r – радиус диска;
l – длина нити.
(R, r, l, mn – величины постоянные, их значения указаны на установке).
Момент инерции платформы, нагруженной исследуемым телом, вычисляется аналогично:
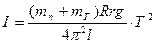 =
= 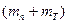 T12 ×К, (3.28)
T12 ×К, (3.28)
где 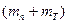 - масса платформы с телом;
- масса платформы с телом;
mT - масса исследуемого тела.
Как видно из выражений (3.27) и (3.28), для определения момента инерции платформы In без тела и момента инерции платформы с исследуемым телом I, необходимо измерить период колебаний крутильного маятника.
Момент инерции исследуемого тела равен разности моментов инерции платформы с исследуемым телом I и без тела In :
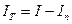 . (3.29)
. (3.29)
В данной лабораторной работе предлагается определить при помощи маятника на трифилярном подвесе момент инерции некоторых тел относительно оси вращения, проходящей через их центр масс, и относительно произвольной оси и проверить теорему Штейнера.
Проверка теоремы Штейнера
1) Определение момента инерции двух цилиндров I2ц относительно оси ОО/, проходящей через их центр масс.
Установить цилиндры друг на друга так, чтобы ось вращения проходила через их центр масс (рисунок 3.11). Измерить период колебаний системы, а затем по формуле (3.28) рассчитать момент инерции системы I1 . Вычислить момент инерции двух цилиндров по формуле (3.29), а одного – по формуле:
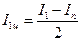 (3.31)
(3.31)
Сравнить его с теоретическим значением (3.12).
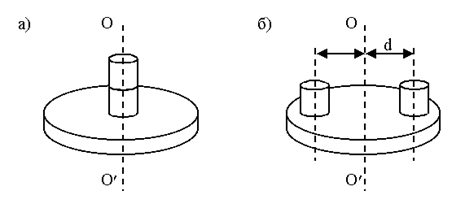
Рисунок 3.11
2) Установить цилиндры симметрично относительно оси ОО/ на расстоянии d (рисунок 3.11).
Определить период колебаний системы. Вычислить момент инерции системы по формуле (3.28) и момент инерции двух цилиндров 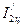 :
:
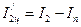 .
.
Определить момент инерции одного цилиндра:
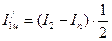 .
.
Сравнить полученное значение 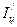 с вычисленным по теореме Штейнера:
с вычисленным по теореме Штейнера:
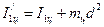 ,
,
где 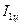 – момент инерции одного цилиндра относительно оси, проходящей через центр масс (формула 3.31),
– момент инерции одного цилиндра относительно оси, проходящей через центр масс (формула 3.31),
mц – масса цилиндра.
3) Вывести формулы абсолютной и относительной погрешности для платформы без тела. Вычислить погрешность измерения для ненагруженной платформы по формуле погрешности.
Все измерения и вычисления занести в таблицу 3.1.
ИЗУЧЕНИЕ СОУДАРЕНИЯ ШАРОВ
Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
Удар (или соударение) – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. При ударе тела испытывают деформацию. Явление удара протекает обычно в сотые, тысячные и миллионные доли секунды. Время соударения тем меньше, чем меньше деформации тел. Так как при этом количество движения тел изменяется на конечную величину, то при соударении развиваются огромные силы.
Процесс удара разделяют на две фазы.
Первая фаза – с момента соприкосновения тел до момента, когда их относительная скорость становится равной нулю.
Вторая фаза – от этого последнего момента до момента, когда соприкосновение тел прекращается.
С момента возникновения деформаций в местах соприкосновения тел начинают действовать силы, направленные противоположно относительным скоростям тел. При этом происходит переход энергии механического движения тел в энергию упругой деформации (первая фаза удара).
Во второй фазе удара, когда относительная скорость стала равной нулю, начинается частичное или полное восстановление формы тел, затем тела расходятся и удар заканчивается. В этой фазе кинетическая энергия системы растет за счет положительной работы упругих сил.
У реальных тел относительная скорость после удара не достигает той величины, которую она имела до удара, так как часть механической энергии необратимо переходит во внутреннюю и другие формы энергии.
Различают два предельных типа удара:
а) удар абсолютно неупругий;
б) удар абсолютно упругий.
Абсолютно неупругий удар (близкий к нему) возникает при столкновении тел из пластических материалов (глина, пластилин, свинец и др.), форма которых не восстанавливается после прекращения действия внешней силы.
Абсолютно неупругим ударом называется удар, после которого возникшие в телах деформации полностью сохраняются. После абсолютно неупругого удара тела движутся с общей скоростью.
Абсолютно упругий удар (близкий к нему) возникает при столкновении тел из упругих материалов (сталь, слоновая кость и др.0, форма которых после прекращения действия внешней силы полностью (или почти полностью) восстанавливается. При упругом ударе восстанавливается форма тел и величина их кинетической энергии. После удара тела движутся с разными скоростями, но сумма кинетических энергий тел до удара равна сумме кинетических энергий после удара. Прямая, совпадающая с нормалью к поверхности тел в точке их соприкосновения, называется линией удара. Удар называется центральным, если линия удара проходит через центры тяжести тел. Если векторы скоростей тел до удара лежали на линии удара, то удар называется прямым.
При соударении тел выполняются два закона сохранения.
1. Закон сохранения импульса.
В замкнутой системе (система, для которой результирующая всех внешних сил равна нулю) векторная сумма импульсов тел 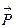 не изменяется, т.е. величина
не изменяется, т.е. величина 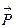 постоянная:
постоянная:
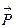 =
= 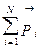 =
= 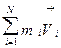 = const, (4.1)
= const, (4.1)
где 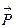 – полный импульс системы,
– полный импульс системы,
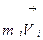 – импульс i –го тела системы.
– импульс i –го тела системы.
2. Закон сохранения энергии
В замкнутой системе тел сумма кинетической, потенциальной и внутренней энергии остается величиной постоянной:
Wк + Wn + Q = const, (4.2)
 где Wк – кинетическая энергия системы,
где Wк – кинетическая энергия системы,
Wn – потенциальная энергия системы,
Q – энергия теплового движения молекул (тепловая энергия).
Простейшим случаем соударения тел является центральный удар двух шаров. Рассмотрим удар шаров массами mi и m2.
Скорости шаров до удара 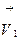 и
и 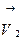 после удара
после удара 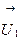 и
и 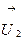 . Для них законы сохранения импульса и энергии запишутся так:
. Для них законы сохранения импульса и энергии запишутся так:
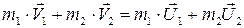 , (4.3)
, (4.3)
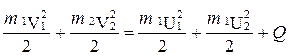 . (4.4)
. (4.4)
Удар шаров характеризуется коэффициентом восстановления К, который определяется отношением относительной скорости шаров после удара 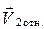 к относительной скорости шаров до удара
к относительной скорости шаров до удара 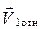 ., взятое по абсолютной величине т.е.
., взятое по абсолютной величине т.е.
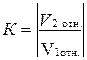 . (4.5)
. (4.5)
Скорости первого шара относительно второго до и после удара равны:
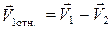 ,
, 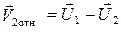 . (4.6)
. (4.6)
Тогда коэффициент восстановления шаров равен:
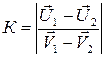 . (4.7)
. (4.7)
При абсолютно упругом ударе выполняется закон сохранения механической энергии, Q = 0, относительные скорости шаров до и после взаимодействия равны и коэффициент восстановления равен 1.
При абсолютно неупругом ударе механическая энергия системы не сохраняется, часть ее переходит во внутреннюю. Тела деформируются. После взаимодействия тела двигаются с одинаковой скоростью, т.е. их относительная скорость равна 0, поэтому коэффициент восстановления тоже равен нулю, К = 0. Закон сохранения импульса запишется в виде
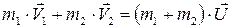 , (4.8)
, (4.8)
где 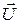 – скорость тел после взаимодействия.
– скорость тел после взаимодействия.
Закон сохранения энергии примет вид:
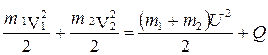 . (4.9)
. (4.9)
Из уравнения (4.9) можно найти Q – механическую энергию, перешедшую во внутреннюю.
На практике предельные случаи взаимодействия осуществляются редко. Чаще взаимодействие носит промежуточный характер, и коэффициент восстановления К имеет значение:
0 £ К £ 1.
Чем ближе значение К к 1, тем меньше доля механической энергии, которая переходит во внутреннюю, тем с меньшей погрешностью удар можно отнести к разряду упругих. К упругим телам относятся, например, сталь, дерево, пластмасса. Коэффициент восстановления стальных шаров 0,8 – 0,9. К пластическим телам относятся глина, пластилин, воск и т.д., коэффициент восстановления для них близок к нулю.
Рассмотрим частный случай, когда массы шаров равны, т.е.
m1 = m2 = m.
Если до взаимодействия первый шар имел скорость V1, а второй был неподвижен (V2 = 0), то по закону сохранения импульса будем иметь:
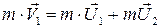 (4.10)
(4.10)
или
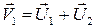 . (4.11)
. (4.11)
Из (4.7) для коэффициента восстановления К имеем:
К = 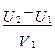 . (4.12)
. (4.12)
Решая совместно уравнения (4.11) и (4.12), получим:
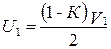 , (4.13)
, (4.13)
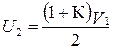 . (4.14)
. (4.14)
В случае абсолютно упругого удара К = 1, тогда U1 = 0, а U2 = V1. Шары при ударе обменивается импульсами. При абсолютно неупругом ударе К = 0 и
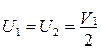 . (4.15)
. (4.15)
Дата добавления: 2021-01-11; просмотров: 398;











