Определение плотности твердых тел правильной геометрической формы
1.6.1 Основные понятия и закономерности
Плотностью тела называют массу тела, объем которого равен единице объема 1 м3.
Средняя плотность тела равна отношению массы тела к его объему 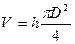 ;
; 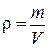 (кг/м3);
(кг/м3); 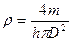 ,
,
где m – масса тела определяется взвешиванием на технических весах;
V – объем тела, находится посредством измерения его линейных размеров штангенциркулем и микрометром.
1.6.2 Порядок выполнения работы
1. Определить высоту цилиндра штангенциркулем.
2. Измерения повторить не менее 3-х раз, каждый раз поворачивая цилиндр.
3. Записать данные измерений в таблицу 1.3.
4. Вычислить среднее значение высоты цилиндра, абсолютную и относительную погрешности.
5. Записать в таблицу 1.3 погрешность прибора.
Таблица 1.3
| № изм. | h, мм | <h>, мм | Dh, мм | <Dh>, мм | Dhпр., мм | Dh = <Dh> + Dhпр., мм |
h = <Dh> ± Dh
e1 = 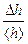 100% 100%
|
6. Прежде, чем пользоваться микрометром, необходимо, чтобы нули шкал (барабана и миллиметровой шкалы) совпадали.
Основным источником ошибок при пользовании микрометром является неравномерность нажатия винта на измеряемый предмет. Для устранения этого недостатка современные микрометры снабжаются специальным приспособлением (трещеткой), не допускающим слишком сильного нажатия (деформации тела).
7. Измерить диаметр цилиндра (проволоки) Д микрометром, повторить измерения 3-5 раз.
8. Вычислить абсолютную и относительную погрешность.
9. Результаты измерений и вычислений занести в таблицу 1.4.
Таблица 1.4
| № изм. | Д, мм | <Д>, мм | DД, мм | <DД>, мм | DДпр., мм | DД = <DД>+ DДпр., мм | e2 = 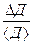 100% 100%
|
| _____________ Д = <DД> ± DД |
В этих таблицах Dh и DД – погрешность отдельных измерений;
<Dh> и <DД> – средняя абсолютная погрешность;
Dhпр иDДпр – погрешность приборная, инструментальная;
e1 = 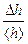 100%; e2 =
100%; e2 = 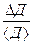 100%.
100%.
10. Измерить массу цилиндра
Dm – абсолютная погрешность измерения массы, вычисляется по таблице 1.5.
11. По формуле 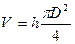 – вычислить объем цилиндра в см3, а затем в м3.
– вычислить объем цилиндра в см3, а затем в м3.
12. По формуле 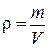 вычислить плотность тела.
вычислить плотность тела.
13. По выведенным формулам вычислить абсолютную, относительную погрешность e плотности и запишите окончательный результат:
r = <r> ± Dr (кг/м3),
e3 = 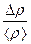 100%.
100%.
Таблица 1.5
| Погрешности гирь | Погрешности гирь | ||
| Номинальное значение | Погрешность | Номинальное значение | Погрешность |
| 10 мг; 20 мг, 50 мг, 100мг | ± 1 мг | 5 г | ± 8 мг |
| 200 мг | ± 2 мг | 10 г | ± 12 мг |
| 500 мг | ± 3 мг | 20 г | ± 20 мг |
| 1 г | ± 4 мг | 50 г | ± 30 мг |
| 2 г | ± 6 мг | 100 г | ± 40 мг |
Основные понятия и закономерности
Вращательным движением тела называется такое движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
При вращательном движении тела изменение его кинематических и динамических характеристик зависит от вращающего момента, действующего на тело, и момента инерции тела.
Основными кинематическими характеристиками вращательного движения являются угловая скорость ω и угловое ускорение ε:
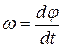 ,
, 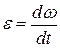 или
или 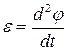 , (2.1)
, (2.1)
где φ – угловое перемещение тела или угол поворота.
Связь между линейной υ и угловой ω скоростями вращающегося тела и линейным аτ и угловым ε ускорениями можно установить, если выразить длину дуги окружности, по которой происходит вращение, через угол поворота φ:
S= φ·r
Тогда:
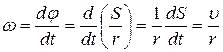 ;
; 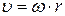 , (2.2)
, (2.2)
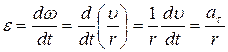 ;
; 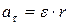 , (2.3)
, (2.3)
где r – расстояние от точки до оси вращения (модуль радиуса – вектора точки).
Угловая скорость ω и угловое ускорение ε – векторные величины. Вектор 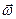 направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а).
направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а).
Направление вектора 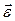 совпадает с направлением вектора
совпадает с направлением вектора 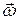 , если
, если 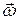 возрастает, и противоположно, если
возрастает, и противоположно, если 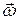 убывает (рисунок 2.1, б, в).
убывает (рисунок 2.1, б, в).
При вращательном движении тела изменение его кинематических и динамических характеристик от момента инерции тела и действующего на тело вращающего момента.
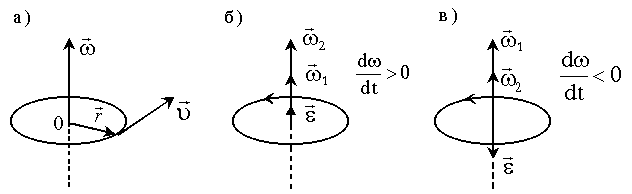
а б в
Рисунок 2.1
Вращающим моментом или моментом вращающей силы называется векторная величина 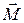 , равная векторному произведению радиуса-вектора
, равная векторному произведению радиуса-вектора 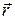 (проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы
(проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы 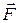 (рисунок 2.2 )
(рисунок 2.2 )
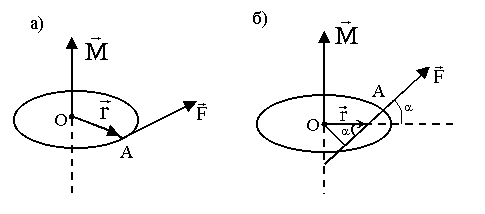
а б
Рисунок 2.2
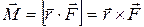 , (2.4)
, (2.4)
где 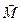 – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 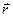 к
к 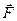 (рисунок 2.2). Векторы
(рисунок 2.2). Векторы 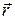 ,
, 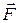 и
и 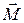 образуют правую тройку векторов.
образуют правую тройку векторов.
Модуль момента силы равен
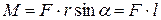 , (2.5)
, (2.5)
где r sinα = l – плечо силы F (рисунок 2.2,б)
l=OC=r sinα – кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила 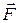 .
.
Твердое тело представляет собой совокупность материальных точек массой mi . Момент сил, действующих на материальную точку, равен
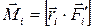 , (2.6)
, (2.6)
где 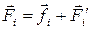 – сумма внутренних
– сумма внутренних 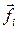 и внешних
и внешних 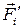 сил, действующих на отдельную точку i (рисунок 2.3).
сил, действующих на отдельную точку i (рисунок 2.3).
Момент сил, действующих на материальные точки:
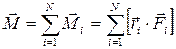 (2.7)
(2.7)
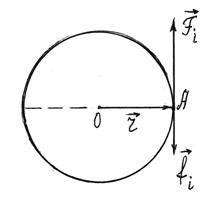
Рисунок 2.3
По второму закону Ньютона 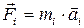 , где
, где 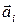 – линейное ускорение материальной точки, связанное с угловым ускорением
– линейное ускорение материальной точки, связанное с угловым ускорением 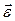 соотношением:
соотношением:
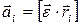 , (2.8)
, (2.8)
следовательно, 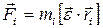 , а момент силы
, а момент силы 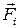 равен
равен
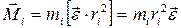 , (2.9)
, (2.9)
где 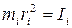 – момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.
– момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.
Соотношение (2.7) можно записать в виде:
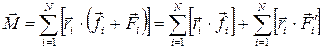 , (2.10)
, (2.10)
где 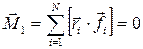 – вращающий момент внутренних сил равен нулю (по третьему закону Ньютона).
– вращающий момент внутренних сил равен нулю (по третьему закону Ньютона).
Поэтому момент внешних сил, действующих на тело, – вращающий момент
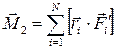 , (2.11)
, (2.11)
Следовательно, учитывая соотношения (2.9) и (2.11), имеем
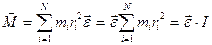 , (2.12)
, (2.12)
где 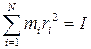 – момент инерции твердого тела относительно данной оси вращения.
– момент инерции твердого тела относительно данной оси вращения.
Момент внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение
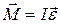 . (2.13)
. (2.13)
Полученное соотношение (2.13) – основной закон динамики вращательного движения.
Из закона динамики вращательного движения следует, что момент силы 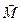 и угловое ускорение
и угловое ускорение 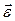 совпадают по направлению.
совпадают по направлению.
Для тела плотностью ρ момент инерции вычисляется суммированием моментов инерции всех его материальных точек:
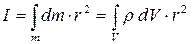 , (2.14)
, (2.14)
где 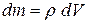 – бесконечно малая масса тела.
– бесконечно малая масса тела.
Момент инерции является физической величиной, характеризующей инертность тела при вращательном движении под действием вращающего момента (аналогично массе тела при поступательном движении, но m = const).
Момент инерции тела зависит от формы тела, его размеров и расположения тела относительно оси вращения.
Момент инерции тела относительно произвольной оси вращения определяется по теореме Штейнера. Момент инерции тела I относительно произвольной оси вращения ОО равен сумме момента инерции тела I0 относительно оси О/О/, проходящей через центр массы тела параллельно оси ОО, и произведения массы тела m на квадрат расстояния d между параллельными осями (рисунок 2.4).
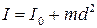 (2.15)
(2.15)
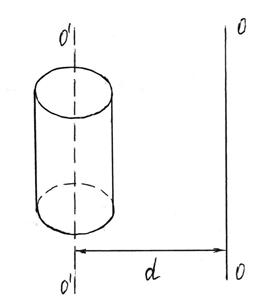
Рисунок 2.4
Теория метода и описание установки
Опытные исследования закона вращательного движения в данной работе проводятся при помощи прибора, (маятник Обербека) изображенного на рисунке 2.5.
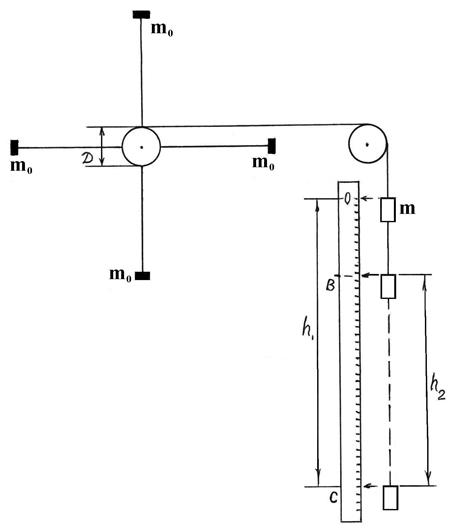
Рисунок 2.5
Он состоит из четырех стержней и двух шкивов, укрепленных на одной горизонтальной оси. Стержни укреплены на одном из шкивов под углом 900 друг к другу. На второй шкив диаметром D намотана нить, к концу которой привязан груз массой m.
По стержням могут перемещаться и закрепляться в нужном положении четыре груза одинаковой массы m0 (по одному на каждом стержне). Грузы закрепляются симметрично так, чтобы центр тяжести совпадал с осью вращения.
Маятник приводится во вращательное движение грузом m. Если дать возможность грузу падать, то вращающий момент, приводящий маятник в движение, создается действием силы натяжения 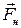 разматывающейся нити (рисунок 2.6).
разматывающейся нити (рисунок 2.6).
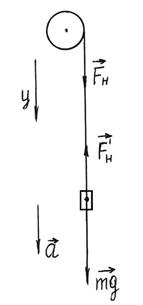
Рисунок 2.6
Если учесть силы трения в подшипниках, за счет которых создается тормозящий момент этих сил, то уравнение движения маятника будет иметь вид:
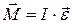 и
и 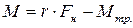 , (2.16)
, (2.16)
которое выражает второй закон Ньютона.
В соотношении (2.16) 
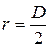 – плечо силы натяжения, D – диаметр шкива, I – момент инерции маятника и деталей, вращающихся с ним (вал, шкив, грузы на нем), ε – угловое ускорение, Мтр. – момент сил трения.
– плечо силы натяжения, D – диаметр шкива, I – момент инерции маятника и деталей, вращающихся с ним (вал, шкив, грузы на нем), ε – угловое ускорение, Мтр. – момент сил трения.
На груз p действуют противоположно направленные силы 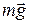 и
и 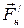 .
.
Уравнение поступательного движения груза на нити имеет вид:
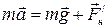 , (2.17)
, (2.17)
где 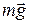 – сила тяжести груза P,
– сила тяжести груза P,
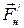 – сила натяжения, действующая на груз со стороны нити.
– сила натяжения, действующая на груз со стороны нити.
В проекциях на ось y , уравнение движения груза можно записать в форме:
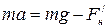 . (2.18)
. (2.18)
Из этого уравнения определяется сила натяжения:
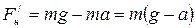 . (2.19)
. (2.19)
К шкиву приложена сила 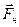 , равная силе натяжения нити
, равная силе натяжения нити 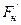 (по третьему закону Ньютона). Подставляя найденную силу Fн в уравнение (2.16), получим:
(по третьему закону Ньютона). Подставляя найденную силу Fн в уравнение (2.16), получим:
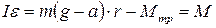 (2.20)
(2.20)
Линейное ускорение падающего груза a определяется из уравнения пути равноускоренного движения:
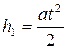 или
или 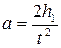 , (2.21)
, (2.21)
где h1 –расстояние, проходимое грузом при падении до нижней точки (h1=ОС, рисунок 2.5),
t – время падения груза.
Тангенциальное ускорение любой точки на боковой поверхности шкива равно ускорению падающего груза. Поэтому угловое ускорение ε определяется соотношением:
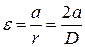 . (2.22)
. (2.22)
Из уравнения (2.20) находим величину момента инерции системы:
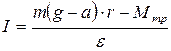 . (2.23)
. (2.23)
Момент инерции вала и шкива ничтожно малы по сравнению с моментом инерции маятника, поэтому полученное уравнение можно считать как расчетную формулу в предлагаемом методе измерения момента инерции I.
Для определения момента инерции по формуле (2.23) необходимо определить момент силы трения в подшипниках. Момент сил трения можно вычислить исходя из следующих соображений. Груз в начальном состоянии (до опускания груза) находится на высоте h1 относительно нижнего положения и имеет потенциальную энергию
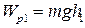 . (2.24)
. (2.24)
Опустившись на полную длину шнура, груз начинает подниматься вверх, а нить будет наматываться на шкив в противоположную сторону (маятник по инерции будет вращаться в прежнем направлении). При этом груз P поднимется на высоту h2 меньшую h1 (h2 = ВС, рисунок 2.5). Потенциальная энергия груза примет значение 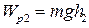 (рисунок 2.5).
(рисунок 2.5).
Уменьшение потенциальной энергии обусловлено тем, что часть ее расходуется на совершение работы против сил трения:
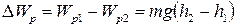 . (2.25)
. (2.25)
Следовательно, имеем:
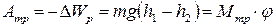 , (2.26)
, (2.26)
где Мтр.·φ – работа сил трения,
Мтр. – момент сил трения,
φ- общий угол поворота маятника за время его движения (от начала движения с высоты h1 от точки О до подъема на высоту h2 до точки В).
Угловое перемещение определяется формулой:
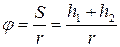 . (2.27)
. (2.27)
Из уравнений (2.26) и (2.27) получим выражение момента сил трения
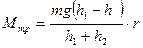 . (2.28)
. (2.28)
По результатам измерений вычислить линейное ускорение а (2.21), угловое ускорение (2.22), момент сил трения (2.28), вращающий момент (2.20), момент инерции по формуле
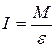 (2.29)
(2.29)
и проверить соотношение:
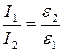 , (2.30)
, (2.30)
где I1 – момент инерции,
ε1 – угловое ускорение движения маятника без грузов,
I2 – момент инерции,
ε2 – угловое ускорение маятника при движении с грузами.
Момент инерции крестовины маятника без грузов находится по формуле (рисунок 2.7)
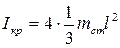 , (2.31)
, (2.31)
где mст – масса стержня,
1/3mстl2 – момент инерции стержня относительно оси вращения, проходящей через его конец,
l – длина стержня.
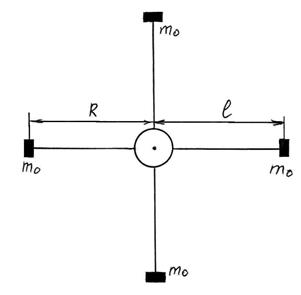
Рисунок 2.7
Момент инерции маятника с грузами определяется как сумма момента инерции крестовины Iкр. и четырех грузов массой m0. Так как размеры грузов малы по сравнению с расстоянием от оси вращения до их центров масс, то момент инерции грузов можно рассматривать как момент инерции материальных точек. Поэтому момент инерции маятника с грузами определяется формулой:
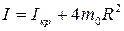 , (2.32)
, (2.32)
где R – расстояние от оси вращения до центра масс грузов.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Вращательное движение характеризуется угловым перемещением φ, угловой скоростью 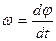 и угловым ускорением
и угловым ускорением 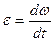 . При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
. При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
Связь линейного и углового перемещений выражается соотношением:
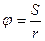 (радиан) (3.1)
(радиан) (3.1)
Тогда 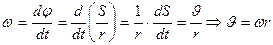 (3.2)
(3.2)
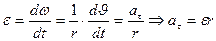 (3.3)
(3.3)
При вращении твердого тела относительно неподвижной оси отдельные его элементарные части с массами 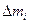 (материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости
(материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости 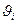 . Но угловая скорость вращения
. Но угловая скорость вращения 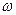 всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
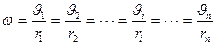 (3.4)
(3.4)
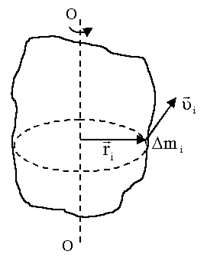
Рисунок 3.1
Кинетическая энергия вращающегося тела Wк определяется как сумма кинетических энергий его составных элементарных масс:
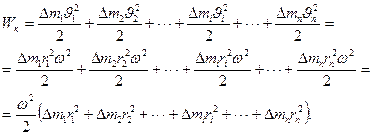 (3.5)
(3.5)
Величину, равную произведению элементарной массы 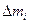 на квадрат расстояния от нее до оси вращения
на квадрат расстояния от нее до оси вращения 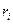 , называют моментом инерции материальной точки
, называют моментом инерции материальной точки
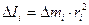 (3.6)
(3.6)
Момент инерции всего твердого тела относительно данной оси вращения равен сумме моментов инерции элементарных масс, составляющих данное тело:
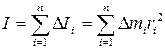 (3.7)
(3.7)
Измеряется момент инерции в кг·м2. Более точно момент инерции можно определить при 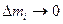 :
:
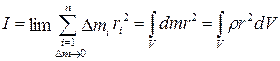 , (3.8)
, (3.8)
где интегрирование производится по всему объему тела.
Из формул (3.5) и (3.7) следует выражение кинетической энергии вращающегося твердого тела:
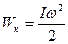 (3.9)
(3.9)
Момент инерции является основной физической величиной, характеризующей инертность твердого тела при вращательном движении.
Момент инерции тела зависит от распределения массы рассматриваемого тела относительно заданной оси вращения (от формы и размеров тела и от расположения оси, относительно которой определяется момент инерции). Для однородных тел правильной геометрической (симметричной) формы момент инерции относительно осей симметрии легко вычисляется.
Рассмотрим момент инерции некоторых тел правильной формы относительно оси симметрии ОО/:
1) Момент инерции материальной точки, т.е. тела, размеры которого много меньше расстояния до оси вращения. Масса тела m ,расстояние до оси вращения ОО/ d (рисунок 3.2):
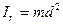 (3.10)
(3.10)
2) Момент инерции тонкостенных колец, цилиндра и обруча относительно оси ОО/ (ri= R) (рисунок 3.3):
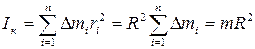 , (3.11)
, (3.11)
где 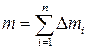 – масса тела;
– масса тела;
R – его радиус.
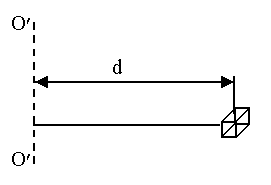
Рисунок 3.2
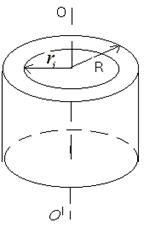
Рисунок 3.3
3) Момент инерции однородного сплошного цилиндра, диска относительно оси ОО/:
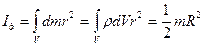 , (3.12)
, (3.12)
где m – масса диска;
R – его радиус.
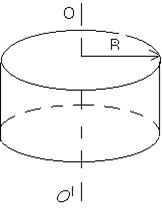
Рисунок 3.4
4) Момент инерции толстостенного кольца относительно оси кольца (рисунок 3.3):
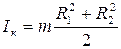 , (3.13)
, (3.13)
где m – масса кольца;
R1 – внутренний радиус;
R2 – внешний радиус.
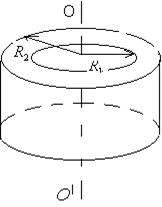
Рисунок 3.5
5) Момент инерции однородного шара относительно оси, проходящей через центр шара:
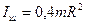 , (3.14)
, (3.14)
где m – масса шара;
R – радиус шара.
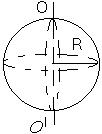
Рисунок 3.6
6) Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно длине l:
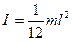 , (3.15)
, (3.15)
где m – масса стержня;
l – длина стержня.
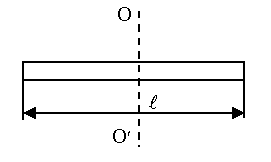
Рисунок 3.7
Из приведенных выше выражений вытекает, что значения моментов инерции тел относительно оси симметрии, проходящей через центр масс, можно представить в виде:
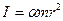 , (3.16)
, (3.16)
где α – коэффициент пропорциональности, зависящий от формы тела.
Если известен момент инерции I0 данного тела относительно оси, проходящей через центр масс этого тела ОО/, то момент инерции I этого тела относительно любой другой оси ХХ/ , параллельной первой и отстоящей от нее на расстоянии а , вычисляется по теореме Штейнера (теорема о влиянии на момент инерции переноса оси вращения)
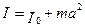 , (3.17)
, (3.17)
где m – масса тела.
Эта теорема может быть выведена непосредственно из определения момента инерции тела относительно произвольной оси (рисунок 3.8).
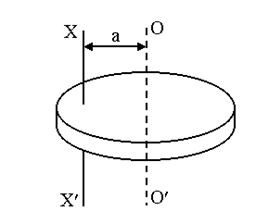
Рисунок 3.8
Дата добавления: 2021-01-11; просмотров: 425;











