Расчет траверс, работающих на сжатие
Траверсы этого типа обычно применяют для подъема царг большого диаметра (рис. 4). В зависимости от нагрузок и длины траверс стержни их могут иметь различные поперечные сечения: сплошные, представляющие собой единичные швеллеры, двутавры и стальные трубы, или сквозные, состоящие из двух швеллеров или двутавров, связанных планками, а также стальной трубы, усиленной уголками.
Траверсы, работающие на сжатие, требуют проверки на прочность и на устойчивость.
Масса траверсы составляет незначительную долю от массы поднимаемого груза (не более 0,01), поэтому в практических расчетах ею можно пренебречь.
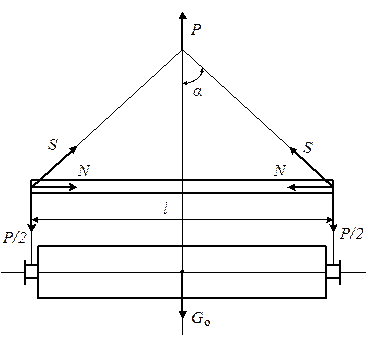
Рис. 4. Траверса, работающая на сжатие
Расчет траверсы производят в следующем порядке:
1. Находят натяжение в каждой канатной подвеске:
S=10·Gо / (2cosα),
где Gо – масса поднимаемого оборудования, т; α– угол наклона тяги к вертикали.
2. По найденному значению S рассчитывают стальной канат.
3. Сжимающее усилие в стержне траверсы с учетом коэффициентов динамичности Кд и перегрузки Кп определяют по формуле:
N=10·Gо tgα Кп Кд/2 .
4. Траверсу рассчитывают на устойчивость как стержень, работающий на сжатие. Для этого в зависимости от величины нагрузки и длины траверсы задаются формой ее поперечного сечения и определяют требуемую площадь:
Fтр=N/(φ m R),
где φ – коэффициент продольного изгиба, значением которого предваритель-
но задаются. Для стержня из швеллера, двутавра или уголка φ = 0,7–0,9; из стальной трубы φ =0,4.
5. Определяют расчетную длину стержня:
lc = μ·l,
где μ – коэффициент приведения расчетной длины, зависящий от условий закрепления концов стержня и приложения нагрузки (прил. 8).
6. Устанавливают гибкость стержня:
для швеллера или двутавра
λх = lc/rх ,
λу = lc/rу ;
для стальной трубы
λ = lc/r .
При этом должно удовлетворяться условие:
max{ λх , λу }≤ [λ],
где rх, rу – радиусы инерции относительно главных осей; [λ] – предельная гибкость (прил. 9).
По наибольшей гибкости, если она не превышает предельную, из
прил. 10 находят коэффициент продольного изгиба φ.
7. Полученное сечение стержня проверяют на устойчивость:
N/(F φ) ≤ mR .
Пример 5. Рассчитать траверсу, работающую на сжатие (см.рис. 4) длиной l=3 м для подъема горизонтального цилиндрического барабана массой Go=36 т, если α=450.
Решение:
1. Находим натяжение в каждой канатной подвеске:
S=10·Go/(2cos α)=10·36/(2·0,707)=254,6кН .
2. Определяем разрывное усилие при условии, что для грузового каната с легким режимом работы Кз=5 (см. прил. 1):
Rк=S·Кз=254,6·5=1273 кН .
3. По найденному разрывному усилию подбираем стальной канат типа ЛК-РО (см. прил. 2) с характеристиками:
временное сопротивление разрыву, МПа…………………..1568
разрывное усилие, кН…………………………………………...1290
диаметр каната, мм…………………………………………….50,5
масса 1000 м каната, кг………………………………………...9440
4. Находим сжимающее усилие в траверсе:
N=10Gо·tgα·Кп Кд/2=10·36·1·1,1·1,1/2=217,8 кН .
5. Для изготовления траверсы принимаем стальную трубу.
6. Задавшись коэффициентом продольного изгиба φ=0,4, находим требуемую площадь поперечного сечения трубы:
Fтр=N/(φm 0,1R)=217,8/(0,4·0,85·0,1·210)=30,5 см2 .
7. По прил. 7 подбираем стальную трубу диаметром 108×10 мм с площадью 30,8 см2 и радиусом инерции r=3,48 см.
8. Находим расчетную длину траверсы, определяя по прил. 8 коэффициент приведения длины μ и считая, что концы траверсы закреплены шарнирно:
lc=μ·l=1·300=300 см .
9. Определяем гибкость траверсы:
λ=lc/r=300/3,48=86,2;[λ]=180; λ ≤ [λ].
10. По прил. 10 находим коэффициент продольного изгиба φ=0,714.
11. Полученное сечение траверсы проверяем на устойчивость:
N / (F·φ) 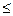 mR ;
mR ;
N / (F·φ)=217,8/ (30,8·0,714)=9,9 кН/см2=99 МПа;
mR=0,85·210=178,5МПа.
Условие выполняется, что свидетельствует об устойчивости расчетного сечения.
- РАСЧЕТ МОНТАЖНЫХ ШТУЦЕРОВ
Для строповки вертикальных цилиндрических аппаратов при их подъеме и установке на фундамент часто применяются монтажные (ложные) штуцеры. Они представляют собой стальные патрубки различных сечений, привариваемые торцом в виде консоли к корпусу аппарата. Для увеличения жесткости внутри штуцера могут быть вварены ребра из листовой стали. Для устранения трения между стропом и штуцером при наклонах аппарата на штуцер надевается свободный патрубок большего диаметра, а для предохранения стропа от соскальзывания к внешнему торцу штуцера приваривается ограничительный фланец.
Расчет монтажного штуцера проводят следующим образом (рис. 5).
1. Находят усилие, действующее на каждый монтажный штуцер:
N=Gо·Кп·Кд·Кн/2,
где Gо – масса поднимаемого оборудования, т.
2. Определяют величину момента от усилия в стропе, действующего на штуцер:
М=N·l,
где l – расстояние от линии действия усилия N до стенки аппарата.
3. При известном сечении штуцера проверяют его прочность на изгиб. Для упрощения расчета наличие ребер жесткости в штуцере не учитывают:
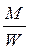 ≤ mR,
≤ mR,
где W – момент сопротивления сечения штуцера (определяется по прил. 7).
4. Если необходимо опреде-
лить сечение штуцера, удовлетво- ряющее условиям прочности, то рассчитывают минимальный мо- мент сопротивления его поперечно- го сечения:
W=M/(mR) .
По прил. 7 для стальных труб находят сечение штуцера с моментом сопротивления, ближай- шим большим к расчетному.
Пример 6. Рассчитать монтажные штуцеры для подъема аппарата колонного типа массой Gо=80 т с помощью двух кранов способом скольжения с отрывом от земли без применения балансирной траверсы. Величина l=120 мм (см.рис. 5).
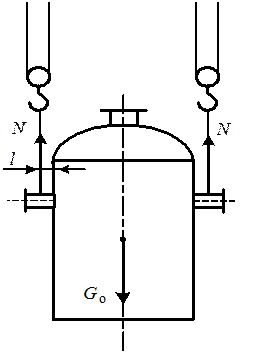
Рис. 5. Расчетная схема монтажного
штуцера
Решение:
1. Находим усилие, действующее на каждый монтажный штуцер при полностью поднятом аппарате:
N=10·Gо·Кп·Кд·Кн/2=10·80·1,1·1,1·1,2/2=580,8 кН.
2. Рассчитываем величину момента, действующего на штуцер:
M=N·l=580,8·12=6969,6 кН·см.
3. Определяем минимальный момент сопротивления поперечного сечения стального патрубка для штуцера:
Wmin=M/0,1·mR=6969,6/(0,1·0,85·210)=390,5 см3.
4. По таблице (см.прил. 7) определяем с запасом сечение монтажного штуцера диаметром 273х12мм, имеющего момент сопротивления
Wт=615 см3, Wт>Wmin.
7. РАСЧЕТ И ПОДБОР ПОЛИСПАСТОВ
Полиспаст является простейшим грузоподъемным устройством, состоящим из системы подвижных и неподвижных блоков, оснащенных стальным тросом.
Один конец троса закрепляется к блоку, другой конец троса, проходя последовательно через ролики блоков в виде сбегающей ветви, идет на барабан лебедки. Полиспаст предназначен для подъема и перемещения груза, а также для натяжения грузовых канатов, вант и оттяжек в том случае, когда масса  поднимаемого оборудования или натяжение превышают тяговые усилия лебедок.
поднимаемого оборудования или натяжение превышают тяговые усилия лебедок.
Расчет полиспаста сводится к расчету усилий на блоки полиспаста (по ним находят технические характеристики блоков), расчету каната для оснастки полиспаста и подбору тягового механизма.
Расчет полиспаста ведут в следующем порядке:
1. Находят усилие на крюке подвижного блока полиспаста (рис. 6):
Pп=Gо+ Gт,
где Gо – масса поднимаемого груза; Gт – масса траверсы.
2. Рассчитывают усилие, действующее на неподвижный блок полиспаста:
Pн=(1,07÷1,2)Рп,
где величина коэффициента, учитывающего дополнительную нагрузку от усилия в сбегающей ветви полиспаста, назначается, исходя из следующих данных:
| Грузоподъемность полиспаста, m | до 30 | от 30 до 50 | от 50 до 200 | более 200 |
| Коэффициент | 1,2 | 1,15 | 1,1 | 1,07 |
3. Исходя из усилия Рн, подбирают подвижный и неподвижный блоки (прил. 11), определяя их технические характеристики.
4. Усилие в сбегающей ветви полиспаста определяют по формуле:
Sп=Pп /(n·η),
где n – общее количество роликов полиспаста без учета отводных блоков; η – коэффициент полезного действия полиспаста, который выбирается по таблице.
5. Определяют разрывное уси-
лие в сбегающей ветви полиспаста,
по которому подбирают канат для его оснастки ( см. раздел «Расчет стальных канатов»).
6. Подсчитывают длину кана- та для оснастки полиспаста:
L=mп (h+3,14dP)+l1+l2,
где h – длина полиспаста в растянутом виде, dP – диаметр роликов в блоках, l1 – длина сбегающей ветви до барабана ле- бедки, l2 – расчетный запас длины каната (обычно выбирается l2=10 м)
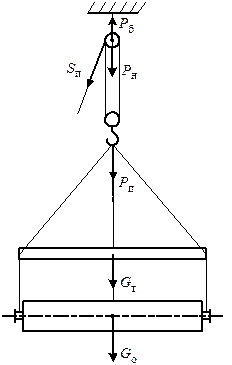
Рис. 6. Расчетная схема полиспаста
Значения коэффициентов полезного действия полиспастовη
| Общее количество роликов полиспаста | Тип подшипника | Общее количество роликов полиспаста | Тип подшипника | ||
| скольжения | качения | скольжения | качения | ||
| 0,960 | 0,980 | 0,638 | 0,800 | ||
| 0,922 | 0,960 | 0,613 | 0,783 | ||
| 0,886 | 0,940 | 0,589 | 0,767 | ||
| 0,351 | 0,921 | 0,566 | 0,752 | ||
| 0,817 | 0,903 | 0,543 | 0,736 | ||
| 0,783 | 0,884 | 0,521 | 0,722 | ||
| 0,752 | 0,866 | 0,500 | 0,708 | ||
| 0,722 | 0,849 | 0,480 | 0,693 | ||
| 0,693 | 0,832 | 0,460 | 0,680 | ||
| 0,664 | 0,814 | 0,442 | 0,667 |
7. Суммарную массу полиспаста рассчитывают по формуле:
Gп=Gб+Gк,
где Gб – масса обоих блоков полиспаста (см.прил. 11), Gк=L·gк/1000; gк – масса 1000 м каната (прил. 2).
8. Определяют усилие, действующее на канат, закрепляющий неподвижный блок полиспаста:
Рб=Gо+Gт+Gп+Sп .
9. По усилию Рб рассчитывают канат для крепления неподвижного блока полиспаста (см. раздел «Расчет стальных канатов»).
10. По усилию в сбегающей ветви полиспаста Sп подбирают тяговый механизм – лебедку (см. прил. 12).
РАСЧЕТ ЛЕБЕДОК
Лебедки применяют при монтажных работах для регулирования положения устанавливаемого на фундамент оборудования, для его оттяжки, а также натяжения вант или наклона мачт, порталов, шевров.
Лебедки позволяют преобразовывать небольшой крутящий момент на привозном валу в значительный крутящий момент на барабане лебедки за счет снижения частоты вращения барабана лебедки.
Лебедка должна быть проверена расчетным путем на устойчивость против смещения и опрокидывания. Устойчивость лебедки обеспечивает балласт – противовес (рис. 7), устанавливаемый на ее раме, либо якорь
(рис. 8).
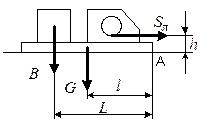
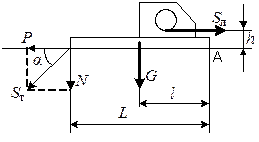
Рис. 7. Расчетная схема Рис. 8. Расчетная схема
крепления лебедки с помощью якорного крепления лебедки
противовеса (балласта)
Расчет лебедки в первом случае сводится к определению необходимой массы балласта. Во втором случае определяется усилие Sт, по которому рассчитывается якорь и элемент крепления лебедки к якорю.
Дата добавления: 2021-01-11; просмотров: 890;











