Фигура и размеры Земли

Определение размеров и фигуры Земли получили свое новое развитие после появления метода триангуляции, который впервые применил голландец Снеллиус в 1615 г. при измерении дуги меридиана в Голландии. С тех пор в разных странах, на разных широтах было измерено много дуг на поверхности Земли и не только по меридианам, но и по параллелям. Все эти измерения показали, что длина дуги 1° меридиана не одинакова под разными широтами: около экватора она равна 110,6 км, а около полюсов — 111,7 км, т.е. увеличивается к полюсам. Это означает, что кривизна земной поверхности меньше в полярных областях, чем в экваториальных. Следовательно, Земля отличается от шара и имеет несколько сплющенную форму, близкую к сфероиду (эллипсоиду вращения).

Для целей геодезии и картографии Землю аппроксимируют сфероидом¾эллипсоидом вращения. На протяжении последних полутора столетий неоднократно определялись элементы земного сфероида, форма которого наилучшим образом согласовывалась с наиболее точными измерениями дуг. Фундаментальные определения были сделаны в СССР Ф.Н. Красовским и А.А. Изотовым в 1940 г. Согласно их исследованиям малая полуось сфероида, совпадающая с осью вращения Земли, равна b = 6356,86 км, а большая полуось, лежащая в плоскости экватора, а = 6378,24 км. Отношение

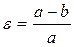называемое сжатием сфероида, равно .

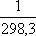В настоящее время размеры и фигура Земли наиболее точно определяется с помощью искусственных спутников Земли (ИСЗ). Принятые международным геодезическим союзом в 1999 г. значения для малой полуоси геоцентрического уровенного эллипсоида b=6356752.3 м, а сжатие a=1/298.2572, что близко к результатам Ф.Н. Красовского и А.А. Изотова.

Рис. 2.4 Геоид, эллипсоид

Истинная фигура Земли отличается и от сфероида, и от трехосного эллипсоида и не может быть представлена ни одной из известных математических фигур. Поэтому, говоря о фигуре Земли, имеют в виду не физическую форму земной поверхности, с океанами и материками, с их возвышенностями и впадинами, а так называемую поверхность геоида (рис. 2.4).

Поверхность, нормалями к которой в любой из ее точек являются отвесные линии, называется уровенной поверхностью, или поверхностью равновесия. Таких уровенных поверхностей, как внутри Земли, так и охватывающих земную поверхность, или пересекающихся с ней, можно провести бесчисленное множество.

Та поверхность равновесия, которая совпадает в открытом океане с поверхностью покоящейся свободной воды, называется геоидом.

Поверхность геоида мало отличается от поверхности земного эллипсоида, как правило, поднимаясь над ней внутри материков и опускаясь в океанах (рис. 40). Разность уровней геоида и наиболее близкого к нему по размерам и форме эллипсоида, исключая немногие места на Земле, меньше 100 м.

Изучение истинной фигуры Земли является одной из основных задач геодезии и гравиметрии и состоит из определения элементов эллипсоида, наиболее близкого к геоиду, и положения отдельных частей поверхности геоида относительно эллипсоида.

Литература к разделу

1. Кононович Э.В., Мороз В.И. Общий курс астрономии. Учебное пособие/Под ред. В.В. Иванова.- М.: Эдиториал УРСС, 2001-544с.

2. Куликовский П.Г. Справочник любителя астрономии. Изд. 5-е - М.:Эдиториал УРСС, 2002. -688с.

3. Ганагина И.Г. Астрономия. - Метод. указ. -Новосибирск: СГГА. - 2002.

4. Зигель Ф.Ю. Сокровища звёздного неба: Путеводитель по созвездиям и Луне. 5-е изд. М.: Наука, 1986- 296 с.

5. Михайлов А.А. Атлас звёздного неба [Электронный ресурс].- 4-е изд.- Л.: Наука, 1978, -17с.- Режим доступа: http://telescop.ucoz.ru/index/0-94. - Загл. с экрана.