Гравитационное взаимодействие.

Тяготение, гравитация, гравитационное взаимодействие – универсальное взаимодействие между любыми видами материи. Сформулированный Ньютоном закон всемирного тяготения справедлив, если взаимодействие относительно слабое и тела движутся со скоростями много меньше скорости света. В общем случае гравитация описывается общей теорией относительности Эйнштейна как воздействие материи на свойства четырехмерного пространства - времени. Эти свойства пространства - времени свою очередь влияют на движение тел и другие физические процессы. Этим гравитация резко отличается от других фундаментальных взаимодействий. Но современная физика считает возможным, что при очень высоких энергиях все виды объединяются в единое взаимодействие [10, с 136, с 772. 11, с 668].

Гипотеза о гравитации как всеобщем свойстве тел появилась в античности и возродилась в XVI и XVII веках в Европе. Например, И. Кеплер утверждал, что «тяжесть есть взаимное стремление всех тел». Окончательно в 1678 г. И. Ньютон в известной работе «Математические начала натуральной философии» дал математическую формулировку закона всемирного тяготения. В такой формулировке закон применим при условии, что тела можно принимать за материальные точки. Численное значение гравитационной постоянной в 1798 г. определил Г.Кавендиш:G = 6.6745(8) * 10^-11 м³ с^-2 кг^-1. Взаимодействие нескольких тел, при условии материальных точек определяется принципом суперпозиции сил. По такому же принципу можно определить силу взаимодействия тел конечных размеров, если предварительно разбить их на части, которые можно считать за материальные точки. Согласно формуле 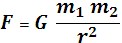(1) сила тяготения зависит только от положения частиц в данный момент времени. Это соответствует условию, что взаимодействие распространяется мгновенно. С учетом конечной, но достаточно высокой скорости распространения взаимодействий, утверждаемой современной физикой, формула (1) может применяться при не высоких скоростях движения и для тел находящихся на не очень больших расстояниях. Такая ситуация имеет место для тел Солнечной системы.

По современным представлениям гравитационное взаимодействие осуществляется через гравитационные поля, существующие вокруг материальных тел. Характеристикой такого поля является напряженность .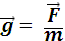

Тогда силу тяготения можно записать:

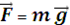
Поле тяготения – потенциальное. g = - grad φ. Знак минус означает, что направление вектора напряженности поля противоположно направлению возрастания потенциала. Если изолированное тело сферически симметрично и если ρ = 0 при r > R, то φ = φ(r), и потенциал поля тяготения материальной точки . Если задано распределение плотности в пространстве, то есть, функция ρ = ρ(r), то потенциал поля можно определить, интегрируя уравнение Пуассона Δφ = 4 π G ρ. Этим объясняется приближение материальных точек в небесной механике, где обычно имеют дело со сферическими телами, находящиеся далеко друг от друга. Точное решение уравнения Пуассона с учетом реального несимметричного распределения масс, используется, например, при изучении строения Земли, методом гравиметрии. Закон тяготения в форме Пуассона используется при теоретическом изучении звезд.

Принципиальные особенности классической теории тяготения Ньютона:

1. В F = m a и в F = m g входит одна масса, т.е. m_И = m_Т

2. Мгновенное значение гравитационного потенциала полностью определяется распределением масс во всем пространстве и предельными условиями для φ на бесконечности. Для ограниченных распределений принимается φ = 0 на r → ∞.

3. Переход от одной ИСО к другой с помощью преобразований Галилея, не изменяет уравнение Пуассона и уравнение движения материальных тел, следовательно, механика Ньютона, включая ньютоновскую силу тяготения, инвариантна к преобразованиям Галилея.

Переход от ИСО к ускоренно движущейся с ускорением (t) (без вращения) не изменяет уравнение Пуассона, но приводит к появлению дополнительного не зависящего от координат члена 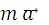в уравнении движения. Точно такой же член в уравнении движения возникает, если в ИСО к гравитационному потенциалу добавить слагаемое, линейно зависящее от координат 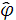'= - 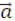(t) т.е. добавить однородное поле тяготения. Таким образом, однородное поле тяготения может быть скомпенсировано в условиях ускоренного движения.

Движение космического корабля (ИСЗ) в поле тяготения Земли, можно рассматривать как движение падающей системы координат. Ускорение космонавтов и всех предметов в корабле относительно Земли одинаково и равно ускорению свободного падения, а относительно друг друга ускорение = 0. Следствием этого является невесомость. Однако, считать относительное ускорение равным 0 можно только если гравитационное поле однородное. При свободном падении в неоднородном гравитационном поле компенсация напряженности поля ускорением не может быть повсеместной. Ускорения соседних свободно падающих частиц не совсем одинаково, ускорение относительно друг друга не равно 0. В космическом корабле относительные ускорения практически не заметны. Так как размеры корабля значительно меньше расстояния от корабля до центра Земли. При этом условии можно считать гравитационное поле в объеме корабля однородным. При достаточно высокой точности экспериментально можно установить неоднородность гравитационного поля, однако при этой же точности всегда можно выделить область размеры которой не позволяют заметить неоднородность. В пределах этой области поле будет выглядеть как однородное.

Неоднородность гравитационного поля не заметная в пределах космического корабля становится заметной в системе Земля – Луна. Не равные нулю относительные ускорения проявляют себя в виде океанских приливов. Сила, с которой Луна притягивает Землю, различна в разных точках Земли. Ближайшие к Луне части водной поверхности притягиваются сильнее, чем центр тяжести Земли, а он притягивается сильнее чем наиболее удаленные части мирового океана. Вдоль линии Луна-Земля относительные ускорения направлены от центра Земли, а в ортогональных (перпендикулярных к этой линии) – к центру. В результате водная оболочка Земли вытягивается в виде эллипсоида вдоль линии Земля – Луна. Из – за вращения Земли по поверхности океана дважды в сутки прокатываются приливные горбы. Неоднородность гравитационного поля Солнца также создает приливную деформацию но ее величина значительно меньше.

Классическая механика Ньютона и его теория тяготения - фундаментальные теории физики. Они позволяют описать с большой точностью обширный круг явлений, в том числе движение искусственных и естественных тел в Солнечной системе и движение в других небесных системах. На основе этих теорий предсказано существование спутника Сириуса, планеты Нептун и др. В астрономии законы тяготения Ньютона являются фундаментом, на основе которого вычисляется движение и строение небесных тел, их эволюция, определяются массы небесных тел. Однако теория Ньютона не согласуется с общей теорией относительности, так как она предполагает мгновенное распространение тяготения. Ее нельзя применять и в сильных полях тяготения, которые разгоняют тела до скорости света. Если тело падает из бесконечности с нулевой начальной скоростью, то следовательно, теория Ньютона применяется если |φ|≪ c², так как должно быть много меньше с.

В полях обычных небесных тел это условие выполняется. Например, вблизи поверхности Солнца ≈ 4 *10^-6 а на поверхности белых карликов ~ 10^-3.

Теория Ньютона не применима, если частица влетела в слабое гравитационное поле, но уже вдали имела (нельзя рассчитать траекторию света в поле тяготения). Она также неприменима при расчете переменного поля тяготения, создаваемого движущимися телами на расстоянии r > λ = cτ (τ – характерное время движения системы (например, период обращения в системе двойной звезды)).

Обобщение теории тяготения на основе специальной теории относительности разработано А. Эйнштейном (1915 -1916 гг.) и представлено в форме общей теории относительности (ОТО). В основу ОТО положена важнейшая особенность поля тяготения, известная в теории Ньютона: ускорение в поле тяготения (ускорение свободного падения) одинаковое для всех тел, независимо от их массы, от химических свойств и др. Это принцип строгой пропорциональности гравитационной m_т(тяжелой) и инертной m_и масс. Гравитационная масса m_т входит в закон тяготения Ньютона, инертная m_и – во второй закон Ньютона. F = m_т g F = m_и a. Если ускорение a сообщает сила тяготения, то m_т g = m_и a; a = g, следовательно m_т = m_и

Равенство масс инертной и тяготения подтверждено различными экспериментами. Отсюда следует глубокая аналогия между движением тел в поле тяготения и движением в отсутствии поля тяготения, но относительно ускоренной системы отсчета. Следовательно, силы инерции в ускоренной системе отсчета эквивалентны гравитационному полю. Это и есть принцип эквивалентности А. Эйнштейна. Можно осуществить и обратную процедуру: можно «уничтожить» в данной точке истинное гравитационное поле введением системы отсчета, движущейся с ускорением свободного падения. В кабине космического корабля (без двигателя), движущегося вокруг Земли в ее поле тяготения, наступает состояние невесомости - не проявляются силы тяготения. Это «слабый» принцип эквивалентности относящийся только к механике. А.Эйнштейн предположил, что все физические процесс в истинном поле тяготения и в ускоренной системе в отсутствии тяготения протекают по одинаковым законам. Это - «сильный» принцип эквивалентности.

Сказанное выше относится к системе отсчета, которая имитирует однородное поле тяготения. Но поля тяготения тел не однородные. Можно рассмотреть истинное гравитационное поле, эквивалентное локальным, соответствующим образом ускоренным в каждой точке, системам отсчета. Тогда в любой конечной области четырехмерное пространство - врем окажется искривленным, неевклидовым. Это означает, что в трехмерном пространстве геометрия неевклидова (сумма углов треугольника и отношение длинны окружности к диаметру не равно π), а время в разных точках течет по-разному. Следовательно, по А. Эйнштейну истинное гравитационное поле есть проявление искривления четырехмерного пространства – времени.

Согласно идее А. Эйнштейна, в поле тяготения все тела движутся по геодезическим (экстремальным) линиям в пространстве - времени, которое искривлено, и поэтому геодезические линии – не прямые. Наблюдатель воспринимает в трехмерном пространстве это движение как движение с переменной скоростью. В заданном поле все тела при одинаковых начальных условиях, будут двигаться по одним и тем же геодезическим линиям (одинаково). Поэтому изменение скорости тел, то есть их ускорение, в данном гравитационном поле одинаково. Одинаковость ускорений тел любой массы и означает строгую пропорциональность m_т и m_и. Кривизна пространства – времени создается источником гравитационного поля. При этом тяготение, то есть искривление пространства и времени, определяется не только массой источника, но и всеми видами энергии, которые есть в системе. Эта идея явилась обобщением принципа эквивалентности массы и энергии (E = m c²) на случай теории тяготения. Тяготение зависит не только от распределения масс в пространстве, но и от их движения, от давления и натяжений, имеющихся в телах, от электромагнитного поля и всех других физических полей.

В теорию тяготения А. Эйнштейна входит вывод СТО о «конечной скорости распространения всех видов взаимодействия». Это означает, что изменение гравитационного поля должно распространятся в пространстве со скоростью с.

В уравнениях Ньютона и Эйнштейна слева стоят величины, характеризующие поле, а справа - величины характеризующие материю, создающую поле. Но у этих уравнений есть различия. В теории Ньютона уравнение Δφ = 4 π G ρ – линейное, следовательно, удовлетворяет принципу суперпозиции. Оно не зависит от движения масс, не определяет их движение. Движение определяется вторым законом Ньютона. В ОТО уравнения не линейны, не удовлетворяют принципу суперпозиции. Решение уравнений Эйнштейна приводит к совместному определению движения материи, которая создает поле, и к вычислению самого поля. При этом уравнения поля тяготения содержит в себе уравнения движения масс в поле тяготения. С физической точки зрения это означает, что в ОТО материя создает искривление пространства – времени, которое влияет на движение материи, создающей это искривление. В случае слабых гравитационных полей метрика пространства – времени мало отличается от евклидовой, и уравнения Эйнштейна приближенно переходят в уравнения Ньютона. В этом случае достаточно малых поправок к уравнениям Ньютона. Эффекты, соответствующие этим поправкам, позволяют экспериментально проверить ОТО. Особенно существенны эффекты ОТО в сильных гравитационных полях. Среди выводов ОТО – существование черных дыр, сингулярностей пространства – времени (то есть мест, где формально, согласно теории, обрывается существование частиц и полей в известной форме) и существование гравитационных волн (гравитационное излучение).

Интересно отметить, что к своим уравнениям ОТО (теория тяготения) А. Эйнштейн добавил космологический член Λ,

[Λ] = см^-2, с целью построения модели Вселенной, не изменяющейся со временем. Это соответствовало существующему в начале XX века представлению о стационарном (статичном, неизменным во времени) состоянии Вселенной. Космологический член или космологическая постоянная Λ может рассматриваться как величина, описывающая плотность энергии, и давление (или натяжение) вакуума. Введенная в 1917 году космологическая постоянная должна была уравновесить тяготение материи, то есть, действовать как антитяготение. Дальнейшие исследования уравнений ОТО А.А.Фридманом (1922 г) показали возможность не статичных решений уравнений ОТО в случае однородного распределения материи, без всякой космологической постоянной. Решение описывало сжимающуюся и расширяющуюся Вселенную. А.Эйнштейн признал правильность переменных относительно времени решений и, таким образом, отсутствие необходимости введения в уравнения космологического члена. Однако, почти через 100 лет идея А. Эйнштейна о космологическом члене, имеющем смысл антигравитации, возродилась в связи с обнаружением разбегания Галактик с ускорением [12].

ОТО - не квантовая теория (как и электродинамика Максвелла). Но гравитационное поле должно подчинятся квантовым законам, как и электромагнитное поле. Иначе было бы противоречие с принципом неопределенности для электронов, фотонов и т.д. С точки зрения квантовой теории гравитационные волны можно рассматривать как поток квантов – гравитонов. Это частицы с нулевой массой покоя, и спином, равным 2 (в единицах ħ). Квантовые эффекты гравитации очень слабы, поэтому в большинстве случаев можно пользоваться не квантовой теорией тяготения А. Эйнштейна. Но квантовые эффекты должны стать очень существенными вблизи сингулярностей поля, где искривление пространства – времени велико. Расстояния, на которых появляются существенные отклонения от геометрии Евклида, называется радиусом r кривизны пространства – времени. Квантовые эффекты гравитации становятся определяющими, если этот радиус становится равным планковской длине:

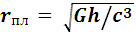≈ 10^{-33 см.}

Сингулярные состояния возникают при гравитационном коллапсе. Они были в прошлом в расширяющейся Вселенной. В сингулярном состоянии при энергиях 1016 эрг.= 109 Дж, все виды физических взаимодействий, по видимому, проявляются как единое. Квантовые эффекты приводят к рождению частиц в поле тяготения черных дыр. Они могут быть важны для черных дыр малой массы (< 1015 г), которые в принципе могли возникать на ранних этапах расширения Вселенной.

В заключение отметим, что в основе ОТО лежит принцип эквивалентности. Он проверялся в опытах Л.Этвеша, Р. Дикке, В.Б.Брагинского, эффекте Р. Мёссбауэра. Ряд опытных проверок связан с Солнцем и Солнечной системой. Например, обе теории тяготения, Эйнштейна и Ньютона, предсказывают искривление луча света при прохождении вблизи массивных тел. Но по ОТО эффект должен быть в 2 раза больше. Наблюдения проводились в периоды полных Солнечных затмений и подтвердили предсказания ОТО (1, 75" с точностью 20%). С отклонением луча связан другой эффект: большая длительность распространения света в поле тяготения Солнца. Дополнительная задержка (больше чем по Ньютону) ~ 2 * 10^-4 с. зарегистрирована. Эксперименты проводились по радиолокации планет Марса и Венеры во время их прохождения за диском Солнца, а также с помощью ретрансляционных сигналов космическими кораблями. ОТО предсказывает медленный дополнительный поворот, (не связанный с гравитационным воздействием других планет) в эллиптической орбите планет, движущихся вокруг Солнца. Наибольший эффект у Меркурия - 43” в 100 лет. Это предсказание подтверждается с точностью до 1%.

Высокая точность этих экспериментов позволяет оценить влияние на массу различных видов энергий связи между частицами тела (дефект масс). Пропорциональность инертной и гравитационной масс означает, что физические взаимодействия внутри тела одинаковым образом участвуют в создании m_Т и m_И. [11, с 671, 672]

Актуализация знаний по фундаментальным взаимодействиям перед изучением Солнечной системы в астрономии должно способствовать более глубокому пониманию не только ее физических основ, но и пониманию всеобщего характера действия физических законов в природе.