ПРИМЕНЕНИЕ АВТОМАТИЗИРОВАННЫХ НАВИГАЦИОННЫХ КОМПЛЕКСОВ 3 глава

В реальных ДИСС с четырехлучевой неподвижной антенной системой лучи расположены симметрично относительно продольной оси самолета и наклонены к плоскости горизонта под одинаковым углом μ (рис. 11). Разностные сигналы лучей 1 и 3, 2 и 4 дают доплеровские частоты f_Д1 и f_Д2, соответствующие лучам 1 и 2. Значения этих частот зависят только от радиальных скоростей сближения самолета с отражающими элементами s1 и s2 земной поверхности, т. е. от проекций путевой скорости самолета W на эти лучи — W_p1 и W_p2,

F_д1=2W_p1/l и F_д2=2W_p2/l,

где λ — длина волны передатчика ДИСС. Но так как

W_p1=Wcos(ψ_л+a)cosm;

W_p2=Wcos(ψ_л-a)cosm,

то

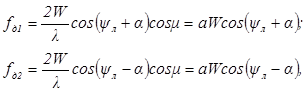
где 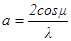— постоянная для данной установки ДИСС величина.

Иначе

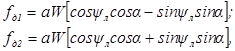
откуда

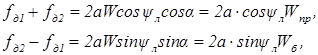
где W_np = Wcosα и W₆ = Wsinα — продольная (по оси самолета и боковая составляющие путевой скорости. Тогда

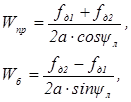
Найдем зависимость проекций W_s и W_z путевой скорости на оси ЧО-системы координат от принимаемых доплеровских частот f_Дl и f_Д2 (рис. 12):

Рис. 12. Разложение скоростей при счислении координат

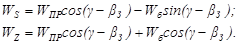
Подставив сюда выражения для W_np и W₆ через f_Д1 и f_Д2, получим:

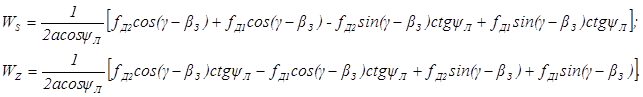
За конечный малый промежуток времени τ (например, 0,1 сек) приращения координат по осям S и Z составят:

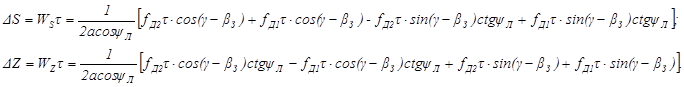
Произведения типа f_д1τ и f_д2τ представляют собой числа N₁ и N₂ периодов доплеровской частоты, принимаемые по лучам 1 и 2 (рис. 8) за промежуток времени τ, т. е. с учетом умножения на соответствующие тригонометрические множители и на общий постоянный коэффициент за скобками дают некоторые части приращений координат ΔS_i и ΔZ_i за этот промежуток времени.

Решение формул в навигационном вычислителе ведется циклами продолжительностью t_Ц ≈ 0,4 сек. В течение одного цикла параллельно определяются приращения ΔS и ΔZ координат.

Цикл состоит из четырех тактов (I, II, III и IV) по 0,1 сек. В течение каждого такта формируется по одному из четырех членов каждой формулы, т. е. какая-то часть приращений координат ΔS_I и ΔZ_I ΔS_II и ΔZ_II и т. д. Таким образом, за один цикл (четыре такта) подсчитывается примерно 1/4 расстояния, пройденного самолетом по осям S и Z. Это учитывается при дальнейшем прохождении информации в вычислителе.

Упрощенная схема решения задачи счисления импульсным методом представлена на рис. 13.

Рис. 13. Блок-схема (упрощенная) счисления координат импульсным методом

По сигналам синхронизирующего устройства вычислителя с ДИСС на вход измерительной схемы через переключатель П₁ поочередно подаются частоты f_Д1 (в тактах II и IV) и f_Д2 (в тактах I и III) в виде последовательностей стандартных импульсов.

В результате в тактах I и III (за 0,1 сек) в схему поступит определенное число импульсов — N₂ = f_Д2τ, а в тактах II и IV — N1 = f_Д1τ.

В такте I со схемы «Формирование временного строба» в устройство «Умножение на строб» подается сигнал, представляющий собой временной строб продолжительностью τ cos (γ — β_З), ограничивающий время подсчета импульсов f_Д2 частью промежутка τ, в результате чего на выходе схемы получается величина f_Д2 τ cos(γ — β₃). Эта величина через переключатель П₃ поступает на реверсивный счетчик импульсов канала S, где преобразуется в последовательность импульсов, управляющих шаговым двигателем ШД_S.

Ось шагового двигателя поворачивается на угол, соответствующий величине принятого сигнала; угол поворота оси двигателя через сельсинную следящую систему передается на счетчик индикатора координаты S.

Одновременно в такте I число импульсов N₂ cos(γ — β₃) со схемы «Умножение на строб» поступает в схему «Умножение на ctg ψ_Л», откуда число импульсов N₂cos(γ — β ) ctg ψ_Л подается на реверсивный счетчик канала Z и далее, преобразуясь в шаговом двигателе в приращение координаты Z, через вторую сельсинную передачу — на счетчик индикатора координаты Z. Так формируется первый член формулы для ΔZ.

В такте II переключается П₁, в результате чего из ДИСС поступает число импульсов N₁ =f_Д1τ, которые далее проходят через схему так же, как и N₂ в такте I (так как переключатель П₃ положения не изменил). В этом такте подсчитываются вторые члены формул.

В такте III переключатель П₁ возвращается в положение такта I, а переключатели П₂ и П₃ переходят в положения III, IV. При этом из схемы «Формирование временного строба» поступает временной строб τ sin(γ — β₃) и умножение на ctg ψ_Л производится в канале 5. В такте III формируются третьи члены формул.

В такте IV переключается только П₁ и формируются четвертые члены.

Итак, в течение tЦ каждого цикла на счетчиках S и Z обновляется информация о текущих координатах самолета.

Необходимая для получения временных стробов величина γ — β3 вырабатывается по текущему курсу у, поступающему из ТКС, и путевому углу β3 ортодромического участка ЛЗП, вводимому вручную в задатчик-индикатор путевого угла (рис. 5).

Аналоговый метод счисления координат в АНК — вспомогательный, применяется при отказах доплеровского датчика для продолжения счисления координат по воздушной скорости (от СВС) и запомненному или введенному вручную ветру.

Счисление координат в главно-ортодромической системе выполняется на тех же элементах АНК аналогично счислению в частно-ортодромических координатах.

Как при импульсном, так и при аналоговом счислении положение продольной оси Оу системы координат (при счислении в ГО) или оси S (при счислении в ЧО) задается установкой на одном из задатчиков путевых углов 5 (рис.5) ортодромического путевого угла, соответствующего выбранному опорному меридиану (относительно которого отсчитывается курс, и на счетчиках координат самолета (1 или 2) — фактических координат х₀ и у₀ (или Z₀ и S₀) самолета в момент включения счисления.

На сигнальных лампочках счетчиков верхней пары в зависимости от выбранной системы координат (ГО или ЧО) подсвечиваются буквенные обозначения х и у (или Z и S).

Одновременно с основным счислением текущих координат самолета в ГО- или ЧО-системе навигационный вычислитель обеспечивает их преобразование.

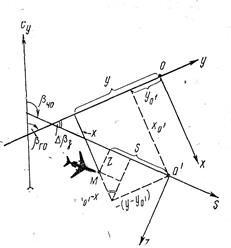Рис. 14. Преобразование ГО-координат самолета в ЧО-координаты

Для преобразования главно-ортодромических координат х и у в частно-ортодромические Z и S относительно отрезка O'S ЛЗП, по которому летит самолет (текущий участок ломаной ЛЗП), необходимо задать параметры новой системы относительно исходной: координаты х₀' и y₀' - начала (очередного ППМ ломаной ЛЗП) и заданный путевой угол β_ЧО оси O'S (рис. 14). Связь между новыми («преобразованными») и исходными («счисленными») координатами устанавливается из рис. 14, если учесть, что продольные координаты у, у₀' и S находятся в области отрицательных значений, а Δβ_З = β_ЧО— β_ГО:

-S=-(y-y_O’)cosΔβ_З+(x_O’-x)sinΔβ_З,

или

S=(y-y_O’)cosΔβ_З+(x-x_O’)sinΔβ_З;

Z=-(y-y_O’)sinΔβ_З+(x-x_O’)cosΔβ_З.

Преобразованные координаты Z и S используются для управления самолетом по текущему боковому уклонению самолета от ЛЗП и для определения момента подхода к ППМ.

Преобразование частно-ортодромических координат Z и S в частно-ортодромические координаты Z' и S' следующего участка ЛЗП выполняются по формулам, получаемым на основании рис. 15:

-S’=-S’_O-[ZsinΔβ_З-(-ScosΔβ_З)];

S’=S’_O+ZsinΔβ_З-ScosΔβ_З;

Z’=-SsinΔβ_З+ZcosΔβ_З.

Как видно из последней формулы, для определения преобразованной координаты Z' по счислимым Z и S достаточно ввести в НВ только величину Δβ_З.. Для определения же преобразованной координаты S' (оставшегося расстояния до следующего ППМ) необходимо, дополнительно задать S'о — длину следующего этапа пути. Постоянное наличие преобразованных координат Z' и S' позволяет в любой момент перейти от стабилизации самолета на текущем участке ЛЗП к выходу на последующий и стабилизации самолета на нем. Переход к полету к следующему участку ЛЗП, включая определение момента начала разворота (на удалении S_УP от ППМ), выполняется автоматически.

Текущие координаты самолета преобразуются также с целью выработки параметров навигационного режима для полета по кратчайшему расстоянию в заданную точку — требуемого путевого угла β_кр и кратчайшего расстояния S_кр.

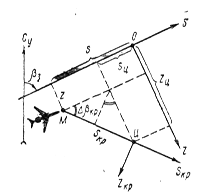
Рис. 15. Преобразование ЧО-координат в ЧО-координаты другого этапа ЛЗП	Рис. 16. Схема решения задачи «КР» при счислении в ЧО координатах

Формулы преобразования в случае счисления в ГО-системе координат получаются, если положить:

x_O'=x_Ц, y_O’=y_Ц, Z=0, Δβ₃=Δβ_КР;

S_КР=(y-y_Ц)cosΔβ_КР+(x-x_Ц)sinΔβ_КР;

0=-(y-y_Ц)sinΔβ_КР+(x-x_Ц)cosΔβ_КР.

При включенном режиме «КР» (рис. 4) по этим формулам непосредственно получаются текущие значения S_КР и Δβ_КР, где Δβ_КР — необходимая поправка к программному значению путевого угла β_З для получения β_КР. Величина β_КР=β₃ + Δβ_КР автоматически отрабатывается на «свободном» (т. е. неиспользуемом в данный момент для счисления) задатчике-индикаторе ПУ 5 (рис. 5), а величина S_КР—на «свободном» счетчике координаты S самолета (1 или 2).

При счислении в ГО-системе β_КР используется для автоматического полета методом управления навигационным режимом с определением (в данном случае) рассогласования между требуемым β_КР и фактическим путевым углом β = γ + α, которое затем приводится к нулю. Величина S_КР используется для контроля пути по дальности и регулирования скорости полета в соответствии с располагаемым временем t_расп.

Если счисление ведется в ЧО-системе координат, то значения Δβ_КР и S_KP получаются на основании рис. 16:

S_КР=(S-S_Ц)cosΔβ_КР+(Z-Z_Ц)sinΔβ_КР;

0=-(S-S_Ц)sinΔβ_КР+(Z-Z_Ц)cosΔβ_КР.

Соотношения по структуре одинаковы с предыдущими выражениями, поэтому решаются с помощью тех же вычислительных устройств, а результаты выдаются также на задатчике-индикаторе ПУ и счетчике координаты S.

По этим β_КР и S_KР строится новый ЧО-участок ЛЗП, на него принудительно переводится счисление и затем выполняется полет методом непосредственной коррекции координаты Z.

Навигационный вычислитель АНК обеспечивает также преобразование высоты полета в параметры управления движением самолета в вертикальной плоскости — разность фактической H и программной H₃ высот или угол θ снижения, определяемый соотношением

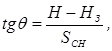
где Н — текущая высота, Н₃ — конечная высота, на которую необходимо выйти с расстояния S_CH. Эти параметры могут быть использованы в САУ для выработки пилотажных команд, индицируемых на позиционных или директорных приборах.

Оптимизация (коррекция) счисленных координат

В АНК с аналоговым вычислителем применяется, как правило, простейший способ оптимизации координат самолета — автоматизированная коррекция с использованием РСБН (неавтономная коррекция) или МНРЛС (автономная коррекция).

При ручной (неавтоматизированной) коррекции значения координат МС, полученные любым способом (от наземной РЛС, визуальным наблюдением и др.), предварительно переводятся в основную систему координат АНК, в которой ведется счисление — х и у или Z и S, а затем вручную устанавливаются на «рабочих» счетчиках.

При автоматизированной коррекции сравниваются полученное независимым методом МС_нез и счисленное МС_СЧ, вырабатываются и индицируются рассогласования ΔZ = Z_НЕЗ — Z_CЧ и ΔS = S_НЕЗ — S_CЧ (или ΔХ и ΔY) между их координатами, по полученным данным принимается решение о целесообразности коррекции и корректирующие поправки ΔZ, ΔS (или ΔХ, ΔY) передаются на рабочие счетчики. Определение корректирующих поправок, их наглядная индикация, а также ввод (после принятия решения) в счетчики осуществляются автоматически. Логическая часть задачи выполняется экипажем, принимающим решение о возможности коррекции в зависимости от степени доверия к координатам, полученным независимым методом, по сравнению со счисленными.

Принцип коррекции ЧО-координат при использовании системы РСБН (или зарубежных маяков VOR/DME) рассмотрим по рис. 16.

Рис. 17. Коррекция координат по данным РСБН

Исходными данными для решения задачи коррекции являются: ЧО-координаты S_p и Z_p радиомаяка, подготовленные при программировании полета; заданный путевой угол β_ИЗ ЛЗП относительно истинного меридиана радиомаяка, также определяемый при программировании; измеренные системой РСБН во время полета истинный пеленг А_C и наклонная дальность D_H самолета относительно радиомаяка; текущая барометрическая высота полета H, поступающая от СВС и принимаемая приближенно отнесенной к уровню радиомаяка. Связь между этими величинами и текущими точными ЧО-координатами S и Z самолета устанавливается по рис. 17, а с учетом соотношения между D_H, H и μ согласно рис. 17, б:

S-S_P=-D_H cosm cosA_PS;

Z-Z_P=-D_H cosm sinA_PS,

или

(S-S_P) secm=-D_H cosA_PS;

(Z-Z_P) secm=-D_H sinA_PS,

где А_PS = А_C + 180° — β_ИЗ — условный пеленг радиомаяка относительно частно-ортодромической оси S, принимаемой за условный меридиан. Инструментовка этих формул производится при помощи нескольких электромеханических (аналоговых) следящих систем, связывающих выходную схему РСБН (А_C, D_H), ручные задатчики ИЗПУ (β_ИЗ) и ЧО-координат радиомаяка (S_p, Z_p), датчик высоты СВС (H), а также специальную схему отработки угла μ, по измеренным текущим D_H и H.

Расхождения между счисленными (Z_CЧ, S_CЧ) и полученными согласно формуле точными (радиотехническими) координатами Z и S для наглядности индицируются на специальном индикаторе (рис. 7, а), если переключатель находится в положении «Индикация»:

ΔZ=Z-Z_СЧ;

ΔS=S-S_СЧ,

После принятия решения на коррекцию установкой переключателя в положение «Коррекция» поправки ΔZ, ΔS вводятся на рабочие счетчики текущих координат самолета и приводят их показания к точным (корректированным) значениям. Изменения показаний счетчиков вызывают управляющее воздействие на самолет со стороны САУ, приводящее к маневру самолета до достижения нулевого показания Z.

При режиме счисления в ГО-системе координат процесс коррекции аналогичен изложенному, но в НВ вводятся не S_P и Z_P, а ГО-координаты y_P и х_P радиомаяка, а на индикаторе поправок отрабатываются значения Δу и Δх, по которым экипаж может судить о возможности выполнения коррекции.

При коррекции с помощью БРЛС используется радиолокационный ориентир (РЛО) с точно определенными при программировании ЧО-координатами. Для наглядного сравнения МС_НЕЗ с МС_СЧ из НВ в БРЛС поступают текущие значения курсового угла ψ_CЧ и наклонной дальности D_НCЧ ориентира, вычисленные по текущим счисленным координатам самолета и запрограммированным координатам РЛО. По ψ_CЧ и D_HCЧ на экране индикатора БРЛС строится электронное перекрестие. Несовпадение изображения РЛО с перекрестием означает расхождение между МС_НЕЗ и МС_СЧ. Ручное наложение перекрестия на изображение РЛО с помощью механизма управления перекрестием (рис. 7, г) позволяет определить поправки к ψ_CЧ и D_HCЧ, а следовательно, и их исправленные значения ψ_РЛО и D_НРЛО, по которым сначала вычисляется условный пеленг РЛО (относительно ЛЗП)

A_РЛО S=ψ_РЛО+γ-β_ИЗ, а затем определяются и корректированные координаты S и Z самолета. Как и при использовании РСБН, величины корректирующих поправок ΔS и ΔZ индицируются на индикаторе поправок.

Кроме оптимизации координат, АНК позволяет при обнаружении систематических боковых ошибок счисления осуществить также коррекцию курсовой системы, для чего используется «блок дискретных поправок» (БДК).

Вопросы студентам:

1. Какие системы САУ работают с аналоговым АНК?

2. Чем отличаются САУ: АБСУ-134А, КА-142, СТУ-154?

3. Какие задачи решает комплекс Путь-4?

4. Какие виды счисления применяются в аналоговых АНК? Какие точнее?

5. Объясните сущность применения ДИСС при счислении.

6. Как вычисляются радиальные скорости самолета?

7. Опишите работу блок – схемы счисления координат импульсным методом.

8. Как преобразуются ГО в ЧО координаты?

9. Как решается задача полета по КР при счислении в ЧО-координатах?

10. Какие виды коррекции применяются в аналоговых АНК? Сравните их точности.

Лекции 9,10,11,12,13.

Режимы управления самолетом

При реализации навигационных решений в полете с АНК возможно несколько режимов управления самолетом: в горизонтальной плоскости — «Основной», «Кратчайшее расстояние», «Курсовая стабилизация» и управление по курсовой зоне посадочного радиомаяка; в вертикальной плоскости — «Вертикальный маневр» и режим управления по радиоглиссаде.

В зависимости от конкретной навигационной обстановки различные сочетания этих режимов позволяют выполнять необходимые маневры.

Основной режим автоматического управления самолетом заключается в стабилизации нулевого бокового уклонения самолета от ортодромической ЛЗП — частной ортодромии. Повышение качества регулирования при этом достигается введением в закон управления самолетом первой производной по времени от бокового уклонения Z, вырабатываемой также в НВ и непрерывно передаваемой в САУ.

Основной режим обеспечивает также автоматический переход па очередной участок ЛЗП. Сигналом к осуществлению перехода является величина оставшегося расстояния (упреждения разворота) S = —S_УР до ППМ. С этого момента начинается управление самолетом по боковому уклонению от следующего участка ЛЗП, что обеспечивается продолжением счисления в новой системе ЧО-координат и выдачей результатов на вторую пару счетчиков (на которых ранее индицировались преобразованные координаты Z' и S', полученные согласно формулам).

Режим «Кратчайшее расстояние»(«КР») — вспомогательный, но широко применяется при автоматическом управлении самолетом. При счислении в ГО-системе он заключается в поддержании фактического путевого угла β, равным непрерывно вырабатываемому в этом режиме требуемому путевому углу β_ТР=β_З+Δβ_З. Следовательно, управление самолетом в этом режиме, в отличие от основного, ведется по схеме следящей системы, непрерывно разворачивающей вектор путевой скорости самолета в требуемое, но заранее не известное положение. При счислении в ЧО-системе режим «КР» позволяет отрабатывать параметры новой ЛЗП (β_КР, S_КР) для управления относительно нее по Z.

В режиме «Курсовая стабилизация» («КС») НВ отключается, а управление самолетом осуществляется с помощью САУ непосредственно от курсовой системы. При этом полет продолжается с постоянным курсом γ_Г, запомненным в момент включения «КС». Курсовая стабилизация применяется для сохранения прежнего навигационного режима на время, пока производятся различные операции со счетчиками координат (ручная коррекция, задание точки для режима «КР»), так как любые изменения показаний этих счетчиков немедленно сказываются (через САУ) на управлении самолетом.

Управление по курсовой зоне наземного посадочного радиомаяка выполняется без использования НВ, с помощью отдельного счетно-решающего устройства командного навигационного комплекса, которое выдает управляющие сигналы на прибор визуальной индикации и в автопилот.

В режиме «Вертикальный маневр» (переключатель на щитке управления устанавливается в положение «ВМ») управление самолетом осуществляется от НВ и заключается в стабилизации угла снижения траектории (θ = const), задаваемого на специальном щитке пилота или штурмана.

Управление по сигналам глиссадного посадочного радиомаяка, так же как и управление по курсовой зоне, выполняется без применения навигационного вычислителя.

Решение задачи захода на посадку

При полете в районе аэродрома навигационный вычислитель вырабатывает данные для маневрирования до входа самолета в зону посадочных радиомаяков, т.е. практически до начала четвертого разворота перед посадкой. Выдерживание направления по оси ВПП и снижение на посадочной прямой выполняются с помощью пилотажных комплексов различных типов («Путь», «Привод» и др.), использующих в этом случае информацию непосредственно от радионавигационных посадочных систем (СП-50, ILS). Однако для повышения надежности выполнения захода на посадку АНК не прекращает выработки всех необходимых данных для выполнения четвертого разворота и для дальнейшего полета по посадочной прямой. Это позволяет при необходимости повторного захода снова перейти к управлению от НВ.

Для построения маневра захода на посадку может быть использован режим «Кратчайшее расстояние» при счислении координат в ГО-системе, привязанной к ВПП аэродрома (рис. 18). Если известны ГО-координаты поворотных точек маневра в зоне аэродрома, то последовательное использование режима «КР» позволяет провести самолет по любой ломаной линии пути до ввода его в зону курсового радиомаяка. Переход к счислению в этой системе координат от ЧО-системы, использовавшейся на маршруте, осуществляется при подходе к зоне аэродрома. Он заключается в преобразовании ЧО-координат самолета на последнем маршрутном участке путем ввода в НВ координат Х_КПМ и Y_КПМ, определенных в ГО-системе с началом в центре ВПП и с направлением ОY главной оси, равным посадочному путевому углу β_ЗП, совпадающим с курсом посадки ψ_ВПП.

Рис. 18. Схема решения задачи захода на посадку с применением АНК, работающего в ГО-системе координат

Для повышения оперативности переходов от одного участка предпосадочного маневра к другому, в АНК входит специальный блок предпосадочного маневра (БПМ), с помощью которого предварительно запоминаются координаты 8—10 точек предпосадочного маневра (ТПМ). Точки вводятся в процессе полета автоматически в вычислитель в установленном при программировании порядке. БПМ (рис. 19) имеет ряд рукояток для ввода координат X и Y ТПМ, тумблер включения режима «Установка программы», переключатель «Прав. — лев.» для выбора направления разворотов при повторном заходе, кнопку принудительной смены ТПМ, а также небольшой планшет для графического изображения предпосадочного маршрута по координатам ТПМ. Ввод координат ТПМ осуществляется с использованием счетчиков задатчика-индикатора координат ППМ 3 (рис. 5). Так как координаты некоторых ТПМ маршрута повторного захода постоянны для всех аэродромов (Х₅₍₉₎ = Х₆ = 0), а также могут повторяться (Х_ТПМ7 = Х_ТПМ8, Y_ТПМ6 = Y_ТПМ7, Y_ТПМ8 = Y_ТПМ5(9)), на БПМ отсутствуют рукоятки для отдельных координат (X ТПМ 5,6, 8 и 9; Y ТПМ 7,8 и 9). Эти координаты вводятся автоматически при установке других, равных им координат; например, при вводе Х_ТПМ7 одновременно вводится Х_ТПМ8, при вводе Y_ТПМ6 — Y_ТПМ7 и т. д.

Рис. 19. Блок посадочного маневра (БПМ)

В полете имеется возможность вручную («принудительно») менять порядок использования ТПМ, пропуская некоторые точки. Сигнал подлета к ТПМ, являющейся вершиной угла «четвертого» разворота (ТПМ5 на рис. 18), играет роль команды на переключение управления самолетом по сигналам курсоглиссадных радиомаяков.

ПРИМЕНЕНИЕ АВТОМАТИЗИРОВАННЫХ НАВИГАЦИОННЫХ КОМПЛЕКСОВ С ЦИФРОВЫМИ ВЫЧИСЛИТЕЛЯМИ

Преимуществами применения в составе АНК бортовых цифровых вычислительных машин (БЦВМ) по сравнению с использованием аналоговых вычислителей являются:

- возможность резкого повышения степени автоматизации навигации за счет реализации большого количества вычислительных и логических операций (задач), что обеспечивает использование точных формул при допустимых габаритах и весе вычислителя;

- практически неограниченные возможности повышения инструментальной точности решения навигационных задач, а также широкие возможности учета методических погрешностей датчиков исходной навигационной информации;

- удобство сопряжения с современными индикаторами, возможность выдачи на индикацию обобщенных (интегральных) навигационных параметров;

- большие возможности автоматического контроля правильности работы как самого вычислителя, так и всех составных частей (систем) комплекса, снижающие затраты времени и облегчающие работу экипажа при подготовке к полету и в самом полете;

- высокая техническая надежность и (в перспективе) небольшая стоимость, достигаемая за счет отсутствия прецизионных элементов и широкой унификации блоков бортового оборудования для АНК различных типов самолетов.

Эти качества делают БЦВМ основой построения современных и перспективных АНК для средних и крупных самолетов гражданской авиации.

ХАРАКТЕРИСТИКА АВТОМАТИЗИРОВАННОГО НАВИГАЦИОННОГО КОМПЛЕКСА С ЦИФРОВЫМ ВЫЧИСЛИТЕЛЕМ

Широкие вычислительные возможности БЦВМ позволяют разрабатывать АНК в различных вариантах, отличающихся как составом датчиков навигационной информации, так и взаимными связями между ними. При этом стараются достичь наиболее точного, надежного и экономичного решения навигационных задач для конкретного типа самолета.

Например, комплексы самолетов «Боинг-747» и «Конкорд» построены в основном на использовании трех инерциальных навигационных систем (ИНС) с вычислителями и бортовой метеорологической РЛС, а в районах аэродромов — радионавигационной системы ближней навигации и посадки (РСБН) VOR-DME-ILS. При этом в их состав не входят ни ДИСС, ни радионавигационная система дальней навигации (РДНС), ни астрономические средства. На других современных самолетах АНК предусматривает сочетание гироинерциальной системы с ДИСС, имеет центральный навигационный вычислитель, а также ряд радионавигационных датчиков информации (РСБН, РСДН, бортовую РЛС). Поэтому о «типовом» АНК с БЦВМ в настоящее время можно говорить только условно, подразумевая такой комплекс, в котором осуществлены наиболее типичные для современного уровня техники способы решения навигационных задач и конструктивные формы.