ПРИМЕНЕНИЕ АВТОМАТИЗИРОВАННЫХ НАВИГАЦИОННЫХ КОМПЛЕКСОВ 1 глава

Ни одно отдельно взятое техническое средство навигации не является универсальным ни по объему решаемых задач, ни по применению в различных условиях навигационной обстановки. Поэтому практикой самолетовождения уже на первых этапах его развития был выработан основной принцип навигационной работы, заключающийся в совместном использовании различных, независимых друг от друга, навигационных средств.

Основная идея этого принципа — достижение наибольшей точности и надежности выполнения операций за счет компенсации недостатков одних датчиков навигационной информации преимуществами других. Например, объединение в курсовых системах магнитного, астрономического и гироскопического датчиков направления обеспечило надежное получение курса самолета практически в любых условиях полета — на прямолинейных участках ЛЗП и на разворотах, в областях нормального поля Земли и вне их, в условиях видимости небесных светил и под облаками.

Возникающие при большом объеме поступающей информации трудности ее обработки преодолеваются всесторонней автоматизацией измерительных, вычислительных и логических операций, т. е. повышением производительности умственного труда экипажей.

ОСНОВЫ АВТОМАТИЗИРОВАННОГО РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ

СОВРЕМЕННЫЕ ПРОБЛЕМЫ ВОЗДУШНОЙ НАВИГАЦИИ

Развитие гражданской авиации и расширение ее применения в различных областях народного хозяйства непрерывно изменяют и условия решения навигационных задач в полете.

Повышение интенсивности воздушного движения предъявляет новые требования к точности навигации в целях предупреждения столкновений между самолетами в воздухе при пересечениях воздушных трасс, а также для обеспечения приема прибывающих в зону аэропорта самолетов. Точная навигация является главным фактором, позволяющим повысить пропускную способность воздушных трасс за счет более плотного бокового, вертикального и продольного эшелонирования.

Для повышения экономической эффективности транспортных полетов дальние рейсы, например через океаны, организуются с выбором оптимального маршрута, учитывающего распределение ветра на трассе. Такие маршруты более сложны для навигационного обеспечения по сравнению с обычными ортодромическими трассами и требуют специальных мер для их успешного выполнения. Влияние экономики проявляется также в тенденции к сокращению летного экипажа, что требует, в частности, обеспечения командира экипажа автоматизированными бортовыми и наземными техническими средствами.

Общая логическая схема навигационного процесса, оставаясь в принципе неизменной, практически реализуется при скоростных и высотных полетах с существенными особенностями, вытекающими из требований к технике и методике навигации конкретных летательных аппаратов. Для обеспечения наибольшей надежности и точности в любых возможных условиях полета на борту современного самолета необходимо иметь несколько независимых датчиков курса и скорости полета, работающих на различных принципах действия, а определение текущих координат вести как методами независимых определений, так и методами счисления. Увеличение числа каналов сбора навигационной информации достигается также путем дублирования некоторых одинаковых датчиков.

Особенности траекторий и временных характеристик движения самолетов требуют выполнения всех вычислительных и логических операций немедленно в реальном масштабе времени или даже с упреждением (прогнозирование хода полета) и тем самым определяют необходимость высокой оперативности при сборе и обработке информации.

Повышенные требования предъявляются также и к пилотированию, которое должно обеспечить высокое качество регулирования режима полета и особенно качество переходных процессов: плавность (апериодичность), краткость (малую постоянную времени), астатизм (отсутствие систематической ошибки по окончании переходного процесса), устойчивость. Для выполнения этих задач необходимы повышение точности и оперативности выработки решений на изменение положения органов управления самолетом и его двигательной установкой.

Реализация отмеченных требований приводит к усложнению информационных процессов на борту летательного аппарата, резкому повышению их объема и темпа.

В связи с развитием средств сбора навигационной информации, усовершенствованием и созданием новых датчиков курса, высоты, скорости, угла сноса, параметров линий положения и других величин экипаж получает такой объем исходных данных, который не может быть полностью использован при решении задачи навигации «ручными» способами, когда основные вычислительные и логические операции выполняются штурманом или пилотом. Это является следствием ограниченных возможностей человека при обработке информации в процессе управления.

Существенным недостатком человека-оператора является также его ограниченная возможность оперировать с многозначными числами, даже при использовании средств механизации счета (линейки, номограммы и т. п.), что непосредственно сказывается на точности результатов.

Из других недостатков человека, как звена в системе управления, следует отметить утомляемость при выполнении однообразных операций, подверженность мешающему воздействию внешних факторов, малую оперативную память.

Все эти недостатки особенно сказываются на тех этапах полета, где навигационные и пилотажные задачи тесно переплетаются между собой (при сложном маневрировании на маршруте и заходе на посадку). Определение целесообразного воздействия на органы управления самолетом на основании показаний навигационных приборов требует в этих случаях быстрого и точного учета таких характеристик движения, как скорости изменения (производные) координат, без чего не обеспечиваются плавный вывод и удержание самолета на программной траектории. Выработка пилотажных решений чисто интуитивным или рефлекторным (приобретенным в процессе предыдущего опыта и тренировок) путем в условиях современных полетов уже себя не оправдывает. Так, при использовании для захода на посадку только нуль-индикаторов курса и глиссады пилот практически не в состоянии точно вести самолет по заданной программе, так как эти приборы не дают информации о скоростях изменения координат.

Применение автоматизации для совершенствования навигации и пилотирования современных самолетов основывается на ряде преимуществ вычислительных устройств по сравнению с человеком-оператором (пилотом или штурманом) при решении задач общей логической схемы навигации.

Эти преимущества следующие: высокая скорость выполнения вычислительных и простейших логических операций, высокая (при применении цифровых машин практически неограниченная) точность вычислений, большая оперативная память и малое время обращения к ней, быстрая реакция на внешние сигналы, меньшая подверженность ошибкам при выполнении многократно повторяющихся операций, отсутствие «усталости».

Однако преимущества автоматических устройств при выполнении конкретных операций навигационного процесса не умаляют ведущей роли человека на пилотируемом летательном аппарате, для которого любая машина является орудием, повышающим производительность труда. Человек обладает целым рядом психофизиологических свойств, позволяющих решать навигационные задачи, как и вообще задачи управления, в условиях, когда машина оказывается неэффективной. К таким свойствам относятся:

большой диапазон принимаемых сигналов;

способность к инициативе в случаях изменения обстановки, требующих творческого решения задачи и выработки суждений в условиях недостаточности поступающей информации;

длительная память, позволяющая учитывать накопленный опыт.

Основными задачами автоматизации навигации являются:

§ сбор первичной информации от всех применяемых в данных условиях датчиков;

§ обработка полученных данных оптимальными способами;

§ полное (по трем координатам) решение навигационной задачи с использованием точных аналитических зависимостей на основе оптимального комплексного использования различных датчиков;

§ решение всех вычислительных и логических задач в реальном масштабе времени, с наименьшим временем запаздывания;

§ обеспечение наглядной и оперативной автоматической индикации внешних условий и навигационных элементов движения самолета;

§ повышение экономичности полетов.

ПРИНЦИП И ОСНОВНЫЕ ОПЕРАЦИИ АВТОМАТИЗИРОВАННОГО НАВИГАЦИОННОГО ПРОЦЕССА

На базе современной техники можно создать автоматическую систему управления, обеспечивающую решение задач воздушной навигации без всякого участия человека. Известны образцы беспилотных самолетов и других летательных аппаратов, навигационно-пилотажное оборудование которых обеспечивает взлет, полет с необходимым маневрированием по заданной траектории и посадку. Однако надежность и стоимость этих средств далеко не соответствуют требованиям гражданской авиации. Поэтому все современные автоматизированные навигационные средства гражданских самолетов развиваются как средства автоматического выполнения возможно большей части функций общей логической схемы навигации под контролем и управлением экипажа, осуществляющего ответственные, но несложные (в основном логические) операции.

Автоматизированным навигационным комплексом (АНК) называется совокупность конструктивно связанных между собой бортовых навигационных средств, обеспечивающих решение экипажем навигационной задачи при совместном использовании нескольких (бортовых, наземных, спутниковых) датчиков исходной информации и автоматическом выполнении вычислительных и части логических операций.

В состав АНК входят следующие характерные группы бортовых средств:

§ датчики навигационной информации (ДНИ);

§ один или два навигационных вычислителя (НВ);

§ устройства управления, индикации и сигнализации (УУИС);

§ вспомогательные устройства (блоки коммутации, специальные источники электропитания и др.).

Решение навигационной задачи заканчивается выработкой сигналов отклонения самолета от заданной пространственно-временной траектории (программы) полета и выбором алгоритма (метода) устранения отклонений с определением регулируемых параметров (z, ż, Δβ, ΔH и т. д.).

Непосредственное управление самолетом осуществляется группой бортовых устройств, составляющих автоматизированный пилотажный комплекс (АПК). Взаимодействие АНК и АПК состоит в том, что АПК, приняв навигационную информацию от АНК, формирует на ее основе командные пилотажные сигналы по крену, тангажу и воздушной скорости и реализует их через автопилот или командно-пилотажные (директорные) приборы. Тесно связанные между собой АНК и АПК составляют в совокупности навигационно-пилотажный комплекс самолета (НПК).

Общая схема работы АНК

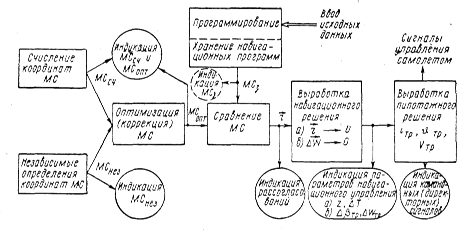Рис. 1. Общая схема решения навигационной задачи в АНК

Общая схема работы АНК (рис. 1) складывается из выполнения следующих основных операций.

Перед полетом производится навигационное программирование, заключающееся в формировании и вводе в память НВ информации, характеризующей заданный пространственно-временной график движения и параметры наземных средств коррекции.

Наиболее совершенные АНК с цифровыми вычислителями требуют ввода только географических координат, высот, времен прохода всех ППМ и координат средств коррекции. Преобразование этих данных в параметры, непосредственно используемые при решении навигационных задач, выполняется в НВ автоматически. В другие АНК (как правило, с аналоговыми НВ) вводятся уже готовые программные данные для каждого этапа полета (путевые углы, расстояния, ортодромические координаты средств коррекции), расчет которых по исходным данным должен выполняться вне АНК при подготовке к полету.

В полете по данным автономных датчиков (доплеровских, инерциальных, аэродинамических) ведется непрерывное счисление текущих координат места самолета (МС_СЧ). Периодически или непрерывно производится определение координат независимыми методами (МС_НЕЗ) с помощью автономных средств (БРЛС, астроориентатора, визуально) или радионавигационных систем (УДНС, РДНС). По результатам независимых определений производится оптимизация текущих координат, определяемых комплексом, которая может выполняться автоматически, полуавтоматически или вручную.

Полученные оптимизированные координаты МС_0ПТ сравниваются с программными (заданными) координатами МС_З, в результате чего определяется вектор рассогласования r или его составляющие — боковое отклонение z самолета от ЛЗП и ошибка ΔS по дальности в текущий момент времени. На основании данных о векторе рассогласования вырабатывается навигационное решение: во-первых, выбирается метод навигации («непосредственная коррекция» или «управление навигационным режимом») и, во-вторых, определяются регулируемые параметры принятого метода.

При методе непосредственной коррекции регулируемыми параметрами, приводимыми к нулевым значениям, являются отклонения текущих координат самолета от их программных значений в данный момент времени: линейное боковое отклонение Z от ЛЗП (ошибка боковой координаты) и расчетное значение ошибки ΔT времени прибытия в контрольную точку (являющееся следствием ошибки ΔS продольной координаты) или угловое уклонение ΔА_С самолета от ЛЗП, заданной как ЛРПС относительно УДНС (РСБН или VOR/DME), а также ошибка ΔT времени прибытия.

Если применяется метод управления навигационным режимом, регулируемыми будут параметры вектора путевой скорости — путевой угол β (или его поправка Δβ) и величина путевой скорости W (или поправка ΔW).

Получаемые текущие значения регулируемых параметров, а часто и их производные (также формируемые в АНК), передаются в пилотажный комплекс для выработки сигналов управления самолетом.

В процессе автоматизированного решения навигационных задач управляющая роль экипажа обеспечивается работой устройств управления, индикации и сигнализации (УУИС), которые позволяют постоянно или периодически (по вызову) получать информацию о текущих координатах, элементах движения, параметрах вектора рассогласования, состоянии основных частей комплекса. На основе этой информации экипаж следит за автоматическим процессом навигации, но при необходимости вмешивается в его ход, используя пульты управления для реализации навигационных решений, выходящих за рамки возможностей автоматики.

Основу АНК и АПК, обеспечивающую им качественно новые возможности по сравнению с другими навигационными средствами, составляют вычислительные устройства, используемые на всех этапах обработки информации. Центральный вычислитель может выполнять не только операции собственно навигационной задачи, но и вычислительную обработку в целях оптимизации первичных измерений (например, курса, путевой скорости), а также автоматический контроль работы датчиков и своих собственных вычислительных схем. Характеристиками вычислительного устройства, примененного в данном АНК, во многом обусловливаются навигационные возможности комплекса в целом.

Переход к автоматизированному решению навигационных задач при использовании многих источников информации требует решения ряда принципиальных вопросов, связанных с выбором основной системы координат АНК, вида аналитических зависимостей для решения навигационных задач, способов отыскания оптимальных значений навигационных параметров и координат МС при наличии избыточной информации, объема и вида необходимой индикации различных навигационных величин, способов управления автоматическими устройствами со стороны экипажа.

Основная система координат АНК

Основной системой координат автоматизированного навигационного комплекса называется система, применяемая в нем для вычислительных операций при счислении координат самолета, их сравнении, коррекциях и выработке управляющих сигналов.

Проблема основной системы координат и связанное с ней навигационное программирование возникли в связи с необходимостью применения аналитических методов обработки информации о координатах самолета, получаемых от нескольких разнородных датчиков — АВК, БРЛС, астроориентаторов, УДНС, РНДС и др. Каждый из этих датчиков выдает координаты в своей специфической системе: АВК и астроориентатор — в географической (геосферической) и ортодромической; БРЛС и УДНС—в полярной относительно различных наземных точек; РДНС — в криволинейной (гиперболической) относительно двух баз наземных станций. При использовании полетной карты была возможность наносить МС в любой системе координат, для чего на ней, кроме географической, строились вспомогательные координатные сетки: биполярная — для УНС; азимутально-дальномерная — для УДНС; гиперболическая — для РДНС; ортодромическая — для АВК ортодромической системы координат и т. д. Тем самым взаимное положение нескольких МС, относящихся к одному времени, но полученных разными путями, было видно непосредственно на карте, их расхождения измерялись линейкой, и для каждого МС легко определялось отклонение от заданной программы, также нанесенной на карту в виде маршрута полета. Однако такой прием совместной обработки информации от различных датчиков не может быть основой автоматического решения навигационных задач главным образом из-за неточности графических построений.

В качестве основной системы координат АНК, как правило, применяется ортодромическая система, связанная либо с ортодромией каждого участка маршрута («частные ортодромии»), либо с одной ортодромией для района полета («главная ортодромия»). На рис. 2 показано расположение на сфере осей главно-ортодромической (Ох и Оу) и частно-ортодромической (OZ и OS) систем координат для одного и того же маршрута. Отсчет продольной координаты (у — в ГО-системе и S — в ЧО-системе) производится от конца этапа, т. е. эта координата имеет отрицательные значения и достигает нуля только в ППМ (КПМ) каждого участка.

Выбор ортодромической системы в качестве основной объясняется тем, что в ней благодаря применению формул плоской тригонометрии проще всего реализуется непрерывное определение текущих координат МС. Кроме того, в этой системе довольно просто обеспечиваются сравнение координат при коррекциях МС по данным радионавигационных средств и выработка навигационных и пилотажных решений, так как одна частно-ортодромическая координата (Z) непосредственно представляет собой боковое отклонение от ЛЗП, а другая (S) — оставшееся расстояние до контрольной точки (ППМ). Наконец, ортодромическая система координат наиболее удобна при использовании навигационного гирополукомпаса (НГПК) — основного курсового прибора современных самолетов гражданской авиации.

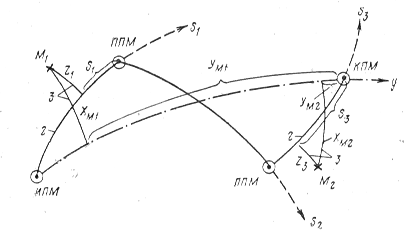
Рис. 2. Главно-ортодромическая (ГО) и частно-ортодромическая (ЧО) системы координат на сфере

Аналитические зависимости для решения задач в АНК

Современная вычислительная техника, особенно цифровая, позволяет реализовать сложные математические зависимости сфероидической геометрии и решать по ним навигационные задачи с любой необходимой степенью точности. Однако невысокая точность исходных данных (особенно при использовании курсовых приборов) позволяет для решения задач воздушной навигации считать поверхность Земли сферической и применять математический аппарат сферической тригонометрии. Этому соответствует и применение в АНК ортодромической системы координат в качестве основной. В то же время все исходные координаты точек на земной поверхности известны только в географической системе, т. е. на эллипсоиде.

В зависимости от требуемой точности замена эллипсоида шаром выполняется различными методами.

В простейшем случае Земля принимается за шар с радиусом R = 6371 км, а геосферические координаты φ и λ считаются равными географическим φ_геогр и λ_геогр; такое упрощение приводит к максимальным ошибкам в расстояниях до 0,5% и в углах — до 0,4°.

В другом случае исходные географические координаты φ_геогр и λ_геогр предварительно с помощью метода проф. В. В. Каврайского переводятся в геосферические по формулам:

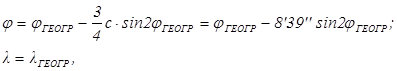
а Земля считается шаром с радиусом R=a(1-c/4)=6372,9 км,

где а = 6378245 м — большая полуось эллипсоида Красовского,

с=(a-b)/a » 1/300 — его сжатие,

b = 6356863 м — малая полуось.

Этот прием обеспечивает уменьшение максимальных ошибок до 0,08% в расстояниях и до 6' — в углах.

Наконец, пересчет географических координат в геосферические можно выполнять по тем же формулам, но радиус Земли выбрать таким, чтобы вдоль заданной ортодромии частный масштаб отображения эллипсоида на сфере был равен единице:

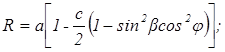
где φ и β — геосферическая широта и путевой угол в любой, в том числе и начальной, точке заданной ортодромии (так как вдоль ортодромии произведение sinβ×cosφ=const). При этом методе достигается точность отображения расстояний до 0,001%.

Однако и сферические зависимости используются часто только для подготовки исходных данных, вводимых в АНК, а само решение навигационных задач ведется по еще более простым зависимостям—формулам прямолинейной тригонометрии. Это обеспечивает значительное упрощение аппаратуры навигационных вычислителей, сохраняя в то же время при определенных условиях вполне удовлетворительную точность результатов.

Возможность применения плоской тригонометрии в навигационных задачах зависит от величин рассматриваемых расстояний, которые лишь в отдельных случаях достигают нескольких тысяч километров (при счислении координат над океаном между коррекциями и при использовании систем дальней радионавигации). При применении же БРЛС, большей части УНС и УДНС ближней навигации расстояния не превосходят 400—500 км.

Представление о степени искажения результатов расчетов при замене сферических треугольников плоскими дает теорема Лежандра, согласно которой углы плоского треугольника со сторонами, равными сторонам сферического, будут уменьшены на 1/3 сферического избытка («эксцесса») данного сферического треугольника:

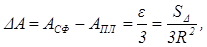
где SΔ — площадь сферического или, приближенно, плоского треугольника, a R — радиус земного шара. Например, при рассмотрении правильного треугольника со сторонами D — 500 км

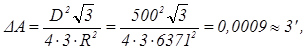
а при сторонах D = 1000 км — ΔА = 12'.

В основе счисления координат по формулам прямолинейной тригонометрии лежит использование упрощенной ортодромической системы координат с таким выбором главной ортодромии (оси Оу), чтобы ЛЗП на всех этапах проходила с возможно меньшими отклонениями от нее. В этих условиях точные («сферические») формулы счисления ортодромических координат при использовании ортодромического датчика курса принимают вид:

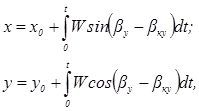
где β_у — текущий условный путевой угол, β_ку — условный «угол карты» (заданный путевой угол главной ортодромии).

Применение в АНК упрощенных формул для счисления координат приводит к методическим ошибкам тем большим, чем больше фактические значения координаты х отличаются от нуля, т. е. при полете по маршрутам, не совпадающим с главной ортодромией. Нетрудно заметить, что при полете по ортодромическим меридианам, т. е. перпендикулярно главной ортодромии (β_у — β_ку = 90°), методическая ошибка отсутствует (так как cos(β_y — β_ку) = 0); наибольшей она будет при полетах с направлениями, близкими к главной ортодромии, но на некотором удалении от нее, когда угол β_у — β_ку близок к нулю. Известны расчеты, на основании которых можно показать, что неучет сферичности Земли в полете по ЛЗП, параллельной в начальной точке главной ортодромии, приводит к относительным радиальным ошибкам счисления МС, определяемым выражением

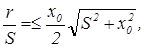
где S — пройденный путь, х₀ — начальное удаление от главной ортодромии, выраженное в радианах (долях радиуса Земли). Например, при S = 500 км = 0,079 рад и х₀ = 200 км — 0,031 рад относительная ошибка МС r/S = 0,0013, а при х₀ = 100 км — r/S = 0,0006.

Однако в условиях полетов гражданской авиации для конкретного заданного маршрута всегда можно выбрать такое положение главной ортодромии, чтобы полет все время проходил вблизи нее, т. е. при малых значениях х, и тем самым практически исключить ошибки счисления, связанные с применением упрощенных формул. Даже в случаях возникновения в полете необходимости резко изменить маршрут в сторону от главной ортодромии современные АНК обеспечивают возможность оперативного перехода на счисление в системе координат, связанной с новой главной ортодромией, т. е. в области малых значений координаты х.

Другая часть вычислительных операций, выполняемых АНК, представляет собой преобразования для перевода координат самолета, определенных различными независимыми методами, в координаты основной системы данного АНК, что необходимо для сравнения их со счисленными или с программными координатами.

В зависимости от применяемых средств (систем) независимого определения МС исходные координаты выражаются в разных системах: географической, биполярной (двуазимутальной), полярной сферической, гиперболической и др. При этом возможен как непосредственный переход от исходных координат к основным, так и через координаты промежуточной системы. Например, гиперболические координаты, определяющие положение МС относительно двух баз станций, могут быть предварительно пересчитаны в географические координаты или в сферические полярные относительно ведущей станции РДНС (ρ, θ), а затем уже в основную систему АНК — ортодромическую.

Применение упрощенных аналитических зависимостей (формул прямолинейной тригонометрии) при координатных преобразованиях допустимо, как правило, только при определении МС с помощью радионавигационных средств (систем) ближнего действия (БРЛС, УДНС ближней навигации), когда опорные ориентиры, используемые при определении МС, удалены от фактического места самолета и от ЛЗП не более чем на 300—350 км. В этих случаях сферические треугольники могут решаться как плоские с такими же сторонами и углами. Возможные при этом ошибки могут быть оценены с помощью теоремы Лежандра.

Вопросы студентам:

1. Каковы основные проблемы современной воздушной навигации. Как они решаются? Приведите примеры.

2. Как решаются задачи в АНК? В чем сущность метода непосредственной коррекции и метод управления навигационным режимом, чем они отличаются?

3. Чем обусловливаются навигационные возможности комплекса?

4. Что такое основная система координат АНК? Какие системы координат применяются в аппаратуре, входящей в АНК? Что такое ГО и ЧО?

5. Что такое сферическая система координат? Что делается для уменьшения ошибки представления геоида в виде сферы?

6. По каким формулам производится счисление ортодромических координат?

7. Как и для чего выбирается ГО? Для чего используется ЧО?

Лекция 5.

Способы оптимизации навигационной информации

Оптимизация исходных навигационных данных (текущих координат и навигационных элементов движения) состоит в том, что из нескольких значений одной и той же величины, полученных с помощью различных датчиков, но относящихся к одному моменту времени, формируется новое, более точное значение этой величины. При этом решение вопроса о том, какое значение измеряемой величины является наиболее точным, т. е. наивероятнейшим, возможно только на основе учета вероятностных характеристик исходных сигналов.

В принципе схема наиболее полной оптимизации состоит в том, что сначала оценивается степень доверия к сигналу каждого отдельного датчика, а затем с учетом этой оценки из всех сигналов составляется такое новое значение измеряемой величины, чтобы оно удовлетворяло некоторому выбранному критерию оптимальности. Критерием оптимальности может служить, например, минимум средней квадратической ошибки искомой навигационной величины.

Сложность оценки каждого из составляющих сигналов заключается в том, что в процессе полета их вероятностные характеристики непрерывно меняются: ошибки АВК растут с увеличением времени полета, ошибки радионавигационных линий положения и МС изменяются в зависимости от удалений от наземных станций систем и других геометрических и физических факторов и т. д.

В настоящее время на основе накопленного опыта автоматизации навигации летательных аппаратов и морских судов разрабатывается общая теория оптимальной обработки навигационных сигналов, имеющая целью обеспечить рациональные алгоритмы получения наивероятнейших значений, как отдельных навигационных величин, так и текущих МС, используемых для навигационного управления самолетом.

При правильной обработке данных точность оптимизированного значения навигационной величины выше наиболее высокой точности исходных величин. Однако осуществление наилучшего способа оптимизации требует сложной бортовой аппаратуры и обеспечивается только при использовании цифровых вычислительных машин. Поэтому в наиболее распространенных в гражданской авиации АНК, имеющих вычислители аналогового типа, задачи оптимизации определения МС решаются упрощенным полуавтоматическим путем, при котором оценка достоверности информации от различных датчиков выполняется штурманом (пилотом), после чего к вычислителю АНК подключается тот датчик координат (параметров), который считается в данных условиях полета наиболее точным. Оптимизация, осуществляемая простой заменой данных менее точного датчика данными более точного, получила название коррекции навигационных данных. Примерами полуавтоматической оптимизации являются периодические коррекции показаний курсовых систем для устранения накапливающейся погрешности курса от собственного ухода гирополукомпасов (режимы «МК» и «АК») или коррекция счисленных координат МС по данным УДНС, БРЛС и других датчиков.