Логические элементы

Устройства, предназначенные для формирования функций алгебры логики, называются логическими устройствами. Логические устройства строятся на логических элементах, которые реализуют определённую функцию. Основные логические операции включают следующие элемен­тарные преобразования двоичных сигналов:

1) Логическое сложение или дизъюнкция (от англ. disjunction - разъединение), обозначаемое символом v и называ­емое также операцией ИЛИ. Эта операция описывается для про­стейшей функции двух переменных х₁ и х₂ в виде логической формулы:

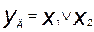
Соотношение означает, что функция y_д равна «1», если хотя бы один из аргументов (х₁ или х₂) равен «1».

Элемент ИЛИ - на выходе этого элемента появится логическая еди­ница тогда, когда хотя бы на одном из входов появится единица. То есть, или на первом, или на втором, или на третьем - на любом из имеющихся входов. Логический ноль на выходе будет только тогда, когда на всех входах будет сигнал логического нуля.

Наиболее просто эту операцию можно реализовать с помощью контактной цепи с дву­мя параллельно включенными контактами. Сигнал y_д на выходе такой цепи появится только в том случае, если хотя бы один из контактов замкнут.

Условное обозначение, таблица истинности и другие показа­тели этой логической функции приведены в таблице 3.

Таблица 3 - Формы отображения основных логических операций

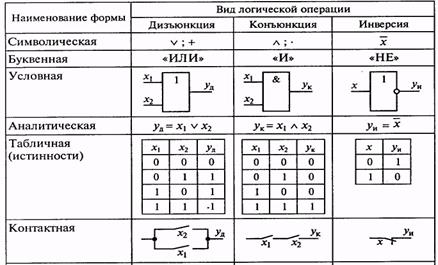
2) Логическое умножение или конъюнкция (от англ. conjunction — соединение), обозначаемое символом ^ и называе­мое операцией И. Условное обозначение & конъюнкции на логи­ческих схемах именуют амперсандом. Для удобства записи сложных логических функций символ конъюнкции можно условно отож­дествлять со знаком обычного умножения. Для функции двух пе­ременных в этом случае имеем:

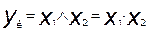
Соотношение показывает, что у_к = 1 только в том случае, когда оба аргумента (х₁ или х₂) становятся равными «1».

Элемент И - на выходе этого элемента сигнал логической единицы появляется только тогда, когда на всех входах будет присутствовать логическая единица. То есть, и на первом, и на втором, и на третьем (если он есть), и на всех имеющихся входах. Если хотя бы на одном входе будет ноль, то и на выходе тоже будет ноль.

Условное обозначение и другие показатели функции у_к пред­ставлены в третьем столбце (см. табл. 3). Эта операция может быть реализована контактной цепью, состоящей из последовательно включённых контактов.

3) Логическое отрицание или инверсия, обозначае­мое черточкой над переменной и называемое операцией НЕ. Эта операция записывается:

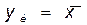
Как видно, операция выполняется над одной переменной x и значение у_и всегда противоположно значению этой переменной. Условное обозначение и другие показатели функции у_и приведе­ны в четвертом столбце (см. табл. 3).

Реализация логической операции НЕ может быть также осу­ществлена контактной цепью, но (в отличие от цепей, рассмот­ренных ранее) с помощью нормально замкнутых контактов элект­ромагнитного реле. Отсутствие напряжения на обмотке реле (x = 0) предполагает замыкание цепи и появление сигнала на ее выходе, соответствующего логической «1» (у_и = 1). При наличии напряже­ния (логической «1») на обмотке реле (х = 1) цепь разомкнута, и сигнал на выходе цепи отсутствует (у_и = 1).

Универсальные логические операции, реализуемые базовыми элементами, включают две следующие разновидности.

4) Функция Шеффера, обозначаемая символически вер­тикальной черточкой | (штрих Шеффера), отображает операцию И-НЕ. Для простейшей функции двух переменных х₁ и х₂ в этом случае полу­чают

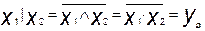
Таблица 4 - Формы отображения универсальных логических операций

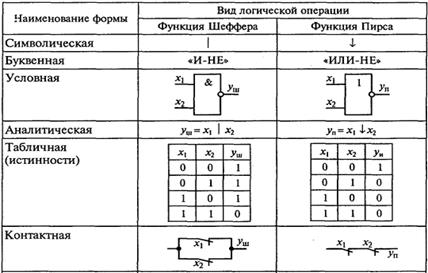
5) Функция Пирса, обозначаемая символически вертикаль­ной стрелкой (стрелка Пирса), выражает операцию ИЛИ-НЕ. Для функции двух переменных х₁ и х₂ она записывается в виде

Важнейшие показатели универсальных логических операций представлены в табл. 4. Реализацию операций И-НЕ и ИЛИ-НЕ не представляет труда осуществить также в контактной цепи, применяя для этой цели электромагнитные реле с нормально замкнутыми (в отсутствие сигнала на входе управления реле, соответствующее отсутствию напряжения на его обмотке) контактами. Для реализации опера­ции И-НЕ электромагнитные реле включают в цепь параллельно (см. табл. 4), а в случае операции ИЛИ-НЕ — последовательно.

Составляя из этих основных кирпичиков различные схемы, можно получить все разнообразие цифровых и логических элементов, применяемых в цифровой технике, которые в свою очередь имеют свои схемные обозначения и выглядят на схеме как самостоя­тельные элементы.