Атака встреча посередине (Meet-in-the-Middle Attack)

При этом методе криптанализа алгоритм шифрования делится на верхнюю и нижнюю части. Затем криптоаналитик посредством частичных (отдельных) рассуждений на базе догадок пытается выполнить частичное шифрование от верха до середины и частичное расшифрование от низа до середины алгоритма. Результаты затем сравниваются и если они согласуются, то ключевой кандидат откладывается (запоминается) для дальнейшего анализа, в противном случае ключевая догадка неправильная. Наиболее примечательные приложения этого метода нашли при анализе каскадных шифров [85, 92, 93]. Далее представляются большие детали.

Атака «встреча посредине» (MITM) требует известного открытого текста и может служить примером метода компромисса между временем и памятью. Рассмотрим операцию двойного DES шифрования 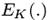с парой (P₁,C₁) известного плайнтекст/шифртекста: 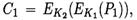которая использует 112-битный ключ (K₁, K₂) с независимыми и равномерно распределенными K₁ и K₂. Это отношение может быть также представлено с помощью операции расшифрования 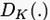как

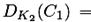
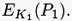
Атака сначала создает список из результатов зашифрований известного открытого текста P₁ для всех 2⁵⁶ возможных кандидатов ключей K’₁ для 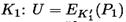и сохраняет пару 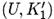в сортированной таблице, проиндексированной с помощью U. Для всех 2⁵⁶ возможных значений K‘₂ ключа K₂ вычисляется 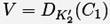и выполняется тестирование V для проверки его присутствия в таблице как индекса. Если V не присутствует в таблице, то 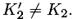Таким же образом продолжается испытание остальных кандидатов для K₂. Если V является индексом для некоторого (U, K’₁), а именно, U = V , то (K’₁, K‘₂) является кандидатом для (K₁,K₂). Для первой пары (P₁, C₁) ожидаемое число ложных сигналов (решений) равно 2⁵⁶/(2⁶⁴/2⁵⁶) = 2⁴⁸, так как существует вероятность 2^-64 совпадения 64-битовых псевдослучайных строк U и V, и 2⁵⁶ значений для K’₁ и 2⁵⁶ значений для K‘₂. Вторая пара плайнтекст/ шифртекста уменьшает интенсивность ложных сигналов до 2⁴⁸× 2^-64 = 2^-16, потому что нужно тестировать только предыдущие 2⁴⁸ кандидатов. Временная сложность атаки равна около 2⁵⁶ + 2⁴⁸ DES шифрований для K₁ и 2⁵⁶ + 2⁴⁸ DES расшифрований для K₂. Сложность памяти равна 2⁵⁶ пар (текст, ключ) для сортированной таблицы и двух известных пар (P;C). Эти вычисления допускают использование одного процессора.

Так как при выполнении каждого зашифрования используются различные ключи, то MITM атака может быть распараллелена с помощью нескольких процессоров. Ван Оршот и Вайнер в [220] описали MITM атаку на базе метода параллельного поиска коллизий и компромисса между временем и памятью (для экономии памяти). Главным преимуществом ее является более короткая (низкая) временная сложность. Их атака требует двух известных пар плайнтекст/шифртекстов. Оцениваемая стоимость аппаратной реализации атаки составляет 10,000,000$ США.

Теперь, пусть 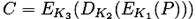будет тройным DES в EDE режиме[1]⁾ с тремя независимыми ключами или 168 ключевыми битами. Атака «встреча посредине» может быть осуществлена аналогично атаке на двойной DES. Допустим, что атака осуществляет поиск коллизий между 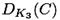и 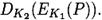Для первой пары (открытый текст, шифртекст), (P₁,C₁), каждый из 2¹¹² кандидатов пар ключей (K’₁, K‘₂) предлагает в среднем 2⁴⁸ раз каждый из 2⁶⁴ 64-битовых текстовых блоков. 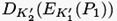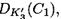И значит, существует 2⁵⁶ совпадений между и или 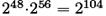кортежей (K’₁, K‘₂, K’₃). Для второй пары (P₂ ,C₂) каждый из 2¹⁰⁴ кандидатов (K’₁, K‘₂, K’₃) имеет вероятность 2^-64 совпадений 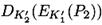с 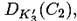и это приводит к генерированию 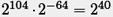кандидатов ключа. Для третьей пары (P₃ ,C₃) каждый из 2⁴⁰ кандидатов (K’₁, K’₂, K’₃) имеет вероятность 2^-64 совпадения 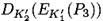с 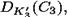и ожидаемое число ложных сигналов равно 2⁴⁰ 2^-64 = = 2^-24. Сложность памяти составляет 2⁵⁶ пар (текст, ключ); требуемыми данными являются три различные пары (P,C), а временная сложность равна 2¹¹² + 2⁴⁸ + 2⁴⁰ шифрований в двойном DES плюс 2⁵⁶ + 2⁵⁶ + 2⁴⁰ расшифрований в одинарном DES.

Ван Оршон и Вайнер в [220] представили распараллеленную версию атаки MITM на трехключевой тройной DES, использующую параллельный метод поиска коллизии и компромисс между временем и памятью.

2.1.7. Метод "Разделяй и побеждай"

Этот метод криптоанализа основан на том, что множество ключей K допускает представление 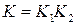. Это значит, что каждый ключ 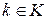может быть представлен в виде вектора 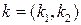, где , .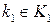

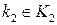Считается также выполненным обязательное условие в виде существования некоторого критерия h, позволяющего при известных открытом и закрытом текстах проверять правильность первого подключа 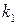в .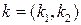

Метод "Разделяй и побеждай" предлагает сначала опробовать элементы множества 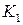, отбраковывая варианты 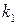по критерию h. Отсюда определяется 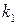- первая компонента вектора 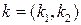. Затем, используя найденное значение 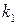и известный шифртекст, опробуются варианты 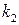. Трудоемкость определения компоненты 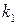равна в среднем 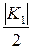операций опробования, соответственно трудоемкость определения 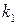равна в среднем 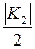операций опробования. Тогда трудоемкость метода есть 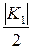+ 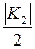против 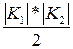при методе полного перебора [4].

Основная проблема при применении метода "Разделяй и побеждай" состоит в нахождении критерия h, который зависит от конкретного преобразования 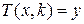, где 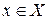, , 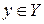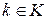или вообще может не существовать. Иногда критерий h может описываться вероятностно-статистической моделью.