Атака на основе коллизии ключей

В [12] Бихам описал атаку с известным открытым текстом на базе парадокса дня рождения. Атака позволяет находить ключ K блочнoго шифра за 2^k/2 запросов (для одного и того же фиксированного открытого текста) со сложностью 2^k/2, где |K|= k битов. Атака допускает, что противник может получить шифровку некоторого фиксированного, известного блока открытого текста, на 2^k/2 случайно выбранных ключах. Такие данные (E_K(P),K) сохраняются в таблице, индексированной первым элементом пары. Каждый шифртекст C’ = E_K’ (P) при известном открытом тексте P сравнивается затем с первыми элементами (C, K) в таблице для некоторого K. Совпадение говорит о том, что кандидат для K’ найден, и сообщения могут быть подделаны, пока K’ остается в применении. Согласно парадоксу дня рождения ожидается, что один из первых 2^k/2 принятых шифртекстов раскрывает свой ключ зашифрования. Если размер блока открытого текста меньше, чем |K|, то могут быть запрошены дополнительные открытые тексты для нахождения уникального решения. Компромиссный алгоритм может вместо этого выбирать m случайных ключей и получать t блоков шифртекстов (при различных ключах, но с одним и тем же открытым текстом).

Вероятность нахождения одного из t ключей равна:

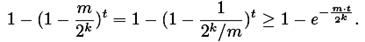
Если 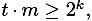то вероятность нахождения ключа равна, по меньшей мере,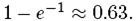

В Таблице 1 показан пример такой атаки с использованием DES. Можно сделать вывод, что теоретическая стойкость шифра ограничена квадратным корнем из размера пространства ключей. Теоретическая стойкость шифра определяется как минимальная сложность t такая, что для заданных t пар плайнтекст/шифртекст, зашифрованных возможно на разных ключах, анализ, занимающий до t шагов, с высокой вероятностью сможет восстановить, по меньшей мере, один из ключей.

Таблица 1. Сложность атаки с коллизией ключей в шифр DES.

# шифротексты

сложность