Методика построения таблиц линейных аппроксимаций подстановочных преобразований.

Под изучением линейных свойств шифров (подстановочных преобразований), в большинстве случаев понимается построение таблиц линейных аппроксимаций подстановок (шифров) и определение их максимумов.

2.3.3.1 Линейная аппроксимационная таблица

Линейная аппроксимация алгоритма шифрования является основой концепции линейного криптоанализа – одного из более важных, общих методов криптоанализа. Под линейной аппроксимацией имеется ввиду линейное уравнение (соотношение), связывающее входные биты подстановки с выходными. Уравнение выполняется с некоторой вероятностью p для случайно выбранного значения маски входа и соответствующей ей маски выхода. Величина |Δp| = |p-1\2| представляет собой эффективность аппроксимации. Аппроксимации с ненулевыми значениями Δp считаются эффективными.

В случае итераивных блочных шифров (именно этот случай нас интересует), расчет наиболее эффективной линейной аппроксимации осуществляется обычно в 2 этапа. Во-первых, вычисляется эффективная линейная аппроксимация одной итерации шифра, как результат композиции аппроксимаций составляющих функций. Далее, как результат композиции аппроксимаций последовательных итераций, получается линейная аппроксимация шифра целиком.

Аппроксимация алгоритма позволяет выявить ключевые биты для достаточно большого набора известных пар открытый текст/зашифрованный текста. В отличии от дифференциального криптоанализа, который по существу является атакой с выбором открытых текстов, линейный криптоанализ относится к атакам с известным открытым текстом и к тому же, в определенных случаях [23], применим к атакам основывающимся исключительно на знании шифртекта.

В общем случае, линейная аппроксимация функции Y = f(X): {0,1}ⁿ —> {0,1 }^m определяется как произвольное уравнение вида:

(2.9)

выполняемое с вероятностью аппроксимации p = N(X',Y')/2ⁿ, где Y' {1,..,m}, X' {1,..,n}, а N(X',Y') обозначает число пар (X, Y), для которых составляется уравнение. Для простоты приведенное выше уравнение записывается в следующем виде:

Y[Y']=X[X'] (2.10)

Множества индексов X',Y' называются входными и выходными масками соответственно, а функция N(X',Y') называется «считающей» функцией аппроксимации.

Характеристика линейной аппроксимации определяется как последовательность (X',Y', p), где X',Y' – маски входа и маски выхода, а p – вероятность аппроксимации.

Линейные аппроксимации произвольной функции, как и в случае с дифференциальным анализом, удобно представлять с помощью специальных таблиц – таблиц линейных аппроксимаций (ЛАТ).

В случае с уменьшенными до 16 бит версиями симметричных шифров, при построении ЛАТ просматриваются всевозможные 16-битные значения входов шифра (открытых текстов), которые получаются при различных 16-битных выходах шифра (шифртекстов). При этом вычисляются поразрядные суммы по модулю 2 произведений входов шифра на некоторые фиксированные числа (входные маски) и соответствующие поразрядные суммы произведений по модулю 2 выходов шифра на фиксированные маски выхода. Входные и выходные маски являются индексами входов в ячейку таблицы размера 2¹⁶×2¹⁶. Сама же таблица получается заполнением ячеек числами, соответствующими количествам линейных соотношений, выполняющихся для композиций входных битов, прошедших маски по столбцам, и выходных битов, прошедших маски по строкам, при вариации по всему множеству входов шифра. Остается заметить, что сущность каждого линейного соотношения заключается в равенстве нулю суммы по модулю 2 входных и выходных бит, прошедших обе маски.

Если маску входов обозначить через α, а маску выходов через β, то число линейных переходов α в β для a-го шифра NS_а(α, β) (число линейных соотношений, выполняющихся для маски входов α и маски выходов β) определяется выражением:

(2.11)

где х – переменная, описывающая входное значение а-го шифра на текущем шаге;

A – величина, равная количеству бит, составляющих вход шифра;

input – количество бит, составляющих вход шифра;

output – количество бит, составляющих выход шифра;

– операция побитового суммирования по модулю 2 одноименных компонент сомножителей (скалярное произведение к-битных векторов).

Алгоритм построения таблицы представлен ниже:

1. построение таблицы 2^m ´ 2^m (m – длина блока);

2. заполнение ячеек значениями -2ⁿ;

3. перебор масок входа и выхода a и b;

4. перебор всех вариантов входа х;

5. вычисление выражения;

HemingWeight(a & X) + HemingWeight(b & Cipher[X]);

6. выполнение инкремента ячейки [a][b], если результат по модулю 2 равен 0;

7. определение максимального значения таблицы.

Вычитание числа, равного половине входов, введено для формирования величин равных смещению относительно половинного (среднего) значения (для того, чтобы представить линеаризованные множества в более простом виде). В результате вероятность р перехода α и β на а-м шифре определятся выражением:

(2.12)

Сложность вычисления одного элемента таблицы ЛАТ, с применением данного алгоритма составляет О(2ⁿ). Учитывая, что в данной работе проводится анализ уменьшенных версий шифров (вход и выход составляют 16 бит), то общая сложность расчета таблицы ЛАТ составляет 2^n+m ·2ⁿ и равняется 2⁴⁸. Данная сложность, на сегодняшний день является достаточно большой, а учитывая тот факт, что в рамках данной работы необходимо построение набора таких таблиц, данный алгоритм является практически не применим.

Для построения таблиц линейных аппроксимаций в данной работе используется ускоренный алгоритм подсчета ЛАТ.

2.3.3.2 Ускоренный алгоритм подсчета ЛАТ

Ускоренный алгоритм подсчета ЛАТ разработан польским ученым Кшиштофом Шмелем из Познаньского Университета Технологий. Он представлен в работе [24] и описывает алгоритм вычисления таблицы аппроксимаций TAf для случайной функции f, определенной в виде .

Пусть TAf – таблица аппроксимаций функции , а TAf₀ , TAf₁ – таблицы аппроксимаций остаточных функций:

 

f₀ = f(Х_n-1 = 0) = f(0, X_n-2,…, X₀) и f₁ = (X_n-1 = 1) = f(1, X_n-2,…, X₀). (2.13)

 

Кроме того, пусть TAf⁰ и TAf¹ обозначают половины TAf для = 0 и = 1 соответственно (рис. 2.1).

 

Рисунок 2.1 – Иллюстрация теоремы 1

Быстрый метод расчета ЛАТ основывается на следующей теореме.

Теорема 1. для произвольной функции f: , где n > 1 и
m ≥ 1 справедливо выражение

TAf⁰ = TAf₀ + TAf₁ , TAf¹ = TAf₀ - TAf₁ (2.14)

Быстрый алгоритм вычисления таблицы аппроксимаций TAf состоит из двух шагов. На первом шаге вычисляется начальное значение таблицы TAf. Процесс получения начального значения TAf включает использование элементарных аппроксимационных таблиц TP всех остаточных функций f, зависящих от одной переменой X₀. На втором шаге вычисляется конечное значение TAf, как результат сложения и вычитания этих элементарных таблиц для последовательных значений. Важной особенностью быстрого алгоритма является то, что вычисление таблицы TAf может быть выполнено поколоночно, без хранения всей таблицы TAf в памяти.

Процедура вычисления начального значения колонки таблицы аппроксимаций TAf для Y´ представлена ниже.

 

INI-TAC(TAC,Y´, f, n, m, TP)

1. for X´ = 0 to do

2. TAC[X´] = BIT-XOR(f[X´] and Y´, m)

3. for X´ = 0 to step 2 do

4. (TAC[X´], TAC[X´+1]) = TP[TAC[X´], TAC[X´+1]]

5. Return

 

Здесь X´, Y´ - маски входа и выхода функции f, TAC (column of approximation table) – колонка аппроксимационной таблицы.

Вспомогательная функция BIT-XOR(X, n) вычисляет вес Хэмминга
n-битного вектора X (количество единиц в двоичной последовательности).

BIT-XOR(X, n)

1. w = 0

2. for i = 0 to n – 1 do w = w

3. return w

Иллюстрация данного алгоритма приводится на рисунке 2.2.

 

Рисунок 2.2–Процедура вычисления начального значения колонки TAf для Y´

 

Начальное значение колонки TAf для Y´ вычисляется процедурой INI-TAC(…). В начале (шаги 1-2) для каждой маски X´ вычисляется значение Y[Y´] с использованием вспомогательной функции BIT-XOR(…) рис.2. Затем (шаги 3-4) каждая пара смежных значений заменяется парой, хранящейся в таблице пар TP. Сама таблица TP представлена в таблице 2.3:

 

Таблица 2.3 – Таблица пар TP

		TP[ , ]
		(1, 0)
		(0, 1)
		(0, -1)
		(-1, 0)

Для каждой функции имеется одна переменная, определяемая значениями и , содержащая пару значений из правой колонки элементарной таблицы аппроксимаций TP.

Алгоритм вычисления конечного значения колонки TAf для Y´ представлен ниже, а также на рисунке 2.3.

CALC-TAC(TAC, i, j)

1. if j – i > 2 then

2. k = (i + j) div 2

3. CALC-TAC(TAC, i, k)

4. CALC-TAC(TAC, k+1, j)

5. SUMSUB-TAC(TAC, i, k, k+1, j)

 

Рисунок 2.3 – Процедура вычисления конечного значения колонки TAf

Конечное значение колонки TAf для Y´ вычисляется рекурсивной процедурой CALC-TAC(…). В первом вызове процедуры должно быть использовано начальное значение колонки TAf и диапазон строк: i = 0, j = . Для диапазона большего 2 задача разбивается на две подзадачи (шаги 3-4). Колонка таблицы аппроксимаций вычисляется вспомогательной процедурой SUMSUB-TAC(…).

SUMSUB-TAC(TAC, , , , )

1. for i = 0 to do

2. (TAC[ + i], TAC[ + i]) = (TAC[ + i] + TAC[ + i], TAC[ + i] – TAC[ + i])

3. return

Процедура SUMSUB-TAC(…) для двух частей колонки TAf (полученных в результате решения двух подзадач) заменяет первую из них их суммой, а вторую – их разностью.

Далее представлен быстрый алгоритм вычисления значения maxTA для функции f:

maxTA(f, n, m)

1. max = 0

2. for Y´ = 0 t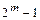o do

3. INI-TAC(TAC, Y´, f, n, m, TP)

4. CALC-TAC(TAC, 0, )

5. for X´ = 0 to do

6. if X´ ≠ 0 or Y´ ≠ 0 then

7. if max < |TAC[X´]| then max = |TAC[X´]|

8. return max

Процедуры INI-TAC(…) и CALC-TAC(…) вычисляют колонку TAf для Y´ за линейное время O(n+m) для одного элемента. Быстрый алгоритм
maxTA(…) вычисляет значение maxTA, которое соответствует лучшей ненулевой линейной аппроксимации функции f. Вычисление производится поколоночно за время O(n+m) для одного элемента. Общая сложность построения ЛАТ составляет 2³² и позволяет применять данный алгоритм на практике (время построения таблицы 2-5 минут, в зависимости от производительности системы).

Содержание заданий и исследований работы. Порядок выполнения исследований

2.4.1. Разработка программного продукта по построению таблицы линейных аппроксимаций подстановочного преобразования

Содержание отчёта

Отчёт должен содержать:

- цель исследований и программу исследований работы;

- разработанный вариант программного комплекса исследования линейных свойств подстановочных преобразований;

- результаты экспериментальных исследований с помощью этого комплекса случайно сгенерированных и заданных преподавателем подстановочных преобразований.

2.6 Контрольные вопросы и задания

1. Дайте определение таблицы ЛАТ подстановки.

2. Назовите известные вам показатели случайности подстановочных преобразований.

3. Приведите определение цикла подстановки.

4. Назовите комбинаторные свойства случайных подстановок.

5. Сформулируйте особенности линейных свойств случайных подстановок.

6. Как определяется линейная вероятность?

7. Изложите методику определения теоретического значения максимума линейной вероятности.

8. Изложите сущность предлагаемого метода определения вероятности получения подстановки с заданным значением смещения.

9. Сущность методики построения линейной таблицы подстановки.

Литература

174. Luke O’Connor. Properties of Linear Approximation Tables. Email: oconnor@dsts. Edu. au, 1995.

175. Luke O’Connor. On Linear Approximation Tables and Ciphers secure against Linear Cryptanalysis. Email: oconnor@dsts. Edu. au, 1995. (семь страниц).

44. Долгов В.И. Свойства таблиц линейных аппроксимаций случайных подстановок. / В.И. Долгов, И.В. Лисицкая, О.И. Олешко // Прикладная радиоэлектроника. - Харьков: ХНУРЭ. – 2010. – Т. 9, № 3. - С. 334-340.

176. Долгов В.И. Анализ циклических свойств блочных шифров. / В.И. Долгов, И.В. Лисицкая, В.И. Руженцев // Прикладная радиоэлектроника. – 2007. – Т.6, №2 – С. 257-263.

177. Nicolas T. Courtois, Gregory V. Bard, and Shaun V. Ault. Statistics of Random Permutations and the Cryptanalysis Of Periodic Block Ciphers, J. Math. Crypt. 2 (2008), 1-20.

171. Бронштейн И.Н. Справочник по математике для инженеров и учащихся вузов. / И.Н. Бронштейн, К.А. Семендяев // Изд-во М:. ²Наука² 1980, 976 стр.

24. Chmiel, K. Fast computation of approximation tables. / К. Chmiel // Information Processing and Security Systems 2005, Part II, 125-134.

[1] Во многих источниках понятия перестановка и подстановка применяются как синонимы.