Элементарная теория дисперсии.
Для качественного понимания многих явлений, возникающих при взаимодействии света с веществом, достаточно учитывать наличие в атомах и молекулах электронов, которые связаны с атомами квазиупруго.
Колеблющийся электрон движется с ускорением, а значит, излучает электромагнитные волны. Вследствие этого колебания электроны будут затухающими.
При прохождении через вещество электромагнитной волны на электроны действует сила, являющаяся вынуждающей:
 . (30.21)
. (30.21)
При этом фаза вынуждающей силы a определяется координатами электрона в веществе.
Амплитуда и фаза вынужденных колебаний под действием вынуждающей силы (30.21) определяется следующими формулами:
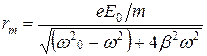 . (30.22)
. (30.22)
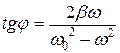 . (30.23)
. (30.23)
w0 – собственная частота колебаний электронов;
b – коэффициент затухания колебаний электронов.
Колеблющиеся электроны излучают вторичные волны, которые распространяются со скоростью света в вакууме с. Но фазы вторичных волн отличаются от фазы первичной. Поэтому при наложении вторичных и первичных волн возникает результирующая волна, распространяющаяся со скоростью 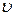 . Различие между
. Различие между 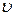 и стем больше, чем меньше знаменатель
и стем больше, чем меньше знаменатель 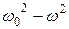 в (30.23) и, соответственно, больше амплитуда вынужденных колебаний, т.е. вблизи резонансной частоты электронов. Отсюда вытекает существование зависимости
в (30.23) и, соответственно, больше амплитуда вынужденных колебаний, т.е. вблизи резонансной частоты электронов. Отсюда вытекает существование зависимости 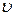 от w, т.е. дисперсии.
от w, т.е. дисперсии.
Для упрощения анализа пренебрежем, в первом приближении, затуханием (потом его наличие мы учтем) т.е. положим b = 0. Тогда амплитуда вынужденных колебаний
 (30.24)
(30.24)
сдвиг фаз между вынуждающей силой и колебаниями 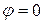 .
.
Следовательно, электроны будут совершать колебания, описывающиеся уравнением:
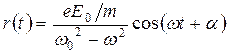 . (30.25)
. (30.25)
Или
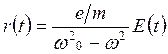 . (30.26)
. (30.26)
При смещении электронов из положения равновесия молекула, как нейтральная в целом система заряженных частиц, приобретает дипольный электрический момент
 . (30.27)
. (30.27)
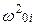 – собственная частота i-го электрона.
– собственная частота i-го электрона.
Напомним, что изменяющийся во времени дипольный электрический момент является источником электромагнитных волн. Каждый из векторов  по направлению совпадает с
по направлению совпадает с 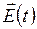 . Поэтому их геометрическое сложение сводится к алгебраическому.
. Поэтому их геометрическое сложение сводится к алгебраическому.
Обозначим число молекул в единице объёма N. Тогда мгновенное значение вектора поляризованности  (дипольного момента единицы объема диэлектрика) можно представить в виде:
(дипольного момента единицы объема диэлектрика) можно представить в виде:
 . (30.28)
. (30.28)
Вектор поляризованности связан с напряженностью поля, в котором находится диэлектрик, соотношением  , где
, где  - диэлектрическая восприимчивость диэлектрика. Диэлектрическая проницаемость вещества eпо определению
- диэлектрическая восприимчивость диэлектрика. Диэлектрическая проницаемость вещества eпо определению
 (30.29)
(30.29)
Но диэлектрическая проницаемость определяет показатель преломления вещества:
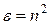 (30.30)
(30.30)
Поэтому можно записать соотношение, определяющее связь показателя преломления и частоты внешнего поля 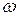 , т .е. волны:
, т .е. волны:
 . (30.31)
. (30.31)
Если частота волны 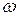 сильно отличается от собственной частоты
сильно отличается от собственной частоты 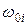 электроновi-го сорта, то сумма в выражении (30.31) мала и
электроновi-го сорта, то сумма в выражении (30.31) мала и  . Вблизи каждой из собственных частот
. Вблизи каждой из собственных частот  обращается в
обращается в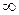 , поэтому графически зависимость
, поэтому графически зависимость  выглядит так, как показано на рисунке 30.6.
выглядит так, как показано на рисунке 30.6.
 Однако бесконечности бессмысленны и возникли они из-за пренебрежения затуханием. В действительности зависимость в окрестности каждой собственной частоты n2(w) имеет вид, показанный приблизительно на рисунке 30.7. Соответственно зависимость от длины волны в соответствующей области длин волн n(l0) имеет вид, показанный приблизительно на рисунке 30.8.
Однако бесконечности бессмысленны и возникли они из-за пренебрежения затуханием. В действительности зависимость в окрестности каждой собственной частоты n2(w) имеет вид, показанный приблизительно на рисунке 30.7. Соответственно зависимость от длины волны в соответствующей области длин волн n(l0) имеет вид, показанный приблизительно на рисунке 30.8.
 Участки 1 – 2 и 3 – 4 соответствуют нормальной дисперсии. На участке 2 – 3 дисперсия аномальная.
Участки 1 – 2 и 3 – 4 соответствуют нормальной дисперсии. На участке 2 – 3 дисперсия аномальная.
В области 1-2 показатель преломления меньше 1, а значит, фазовая скорость больше с. Этот вывод не противоречит теории относительности. Монохроматическая волна не передаёт сигнала. Сигнал передаётся групповой скоростью группы волн. А эта скорость в области 1 – 2 оказывается меньше скорости света в вакууме. В области аномальной дисперсии поглощение очень велико и понятие групповой скорости теряет смысл. Расчеты показывают, что и в этой области энергия, а значит и сигнал, передаются со скоростью меньшей с.
Поглощение света.
При этом прохождение световой волны через вещество часть её энергии затрачивается на возбуждение колебаний электронов. Вторичные волны возвращают затраченную энергию волне, но не полностью. Определенная доля энергии первичной волны преобразуются в другие виды энергии – в энергию движение атомов, т.е. внутреннюю энергию.
Следовательно, интенсивность света при прохождении через вещество уменьшается. Вынужденные колебания становятся особенно интенсивными на резонансных частотах электронов. Поэтому поглощение света особенно велико в области аномальной дисперсии.
Экспериментально установлено, что изменение интенсивности 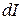 на пути
на пути 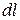 пропорционально
пропорционально 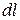 и I:
и I:
 . (30.32)
. (30.32)
где  – коэффициент поглощения.
– коэффициент поглощения.
Если на входе в вещество имеем I0, а после прохождения расстояния l – I, то, интегрируя (30.32), найдём:
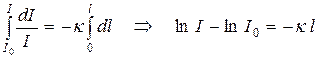
Проведя потенцирование, получаем соотношение:
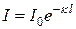 , (30.33)
, (30.33)
которое называется законом Бугера. Из (30.33) следует, что  – величина обратная толщина слоя, в котором интенсивность света I убывает в е раз.
– величина обратная толщина слоя, в котором интенсивность света I убывает в е раз.
Коэффициент поглощения зависит от длины волны: 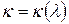 . В газах, где молекулы взаимодействуют очень слабо для большинства длин волн
. В газах, где молекулы взаимодействуют очень слабо для большинства длин волн 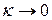 ,но имеются узкие спектральные полосы с резкими максимумами.
,но имеются узкие спектральные полосы с резкими максимумами.
Эти максимумы соответствуют резонансным частотам колебаний электронов в атомах.
Твёрдые тела жидкости и газы при высоких давлениях дают широкие полосы поглощения, которые обусловлены взаимодействием атомов в веществе.
Рассеяние света
С классической точки зрения рассеяние света обусловлено возбуждением колебаний электронов в атомах. Колеблющиеся электроны становятся точечными источниками вторичных волн, которые распространяются по всем направлениям. Однако необходимо учесть, что вторичные волны являются когерентными и соответствующий расчет показывает, что в случае однородной среды вторичные волны полностью гасят друг друга во всех направлениях, кроме направления первичной волны.
Таким образом, рассеяние света возникает только в неоднородной среде. Световые волны дифрагируют на неоднородностях среды и начинают распространяться по всем направлениям. Такую дифракцию на мелких неоднородных и называют рассеянием.
Убывание интенсивности при рассеяние характеризуют коэффициентом экстинкции 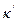 , который добавляется и коэффициенту поглощения:
, который добавляется и коэффициенту поглощения:
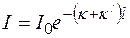
Если величина неоднородностей мала по сравнению с длиной волны, то интенсивность рассеянного света оказывается пропорциональной четвёртой степени частоты:

Это утверждение называют законом Релея.
Даже тщательно очищенные газы и жидкости не являются вполне прозрачными. В них тоже происходит рассеяние света, обусловленное появлением неоднородностей. Неоднородностями являются флуктуации плотности вещества, обусловленные тепловым движением. Такое рассеяние света называют молекулярным. Именно им объясняется голубой цвет неба.
31. КВАНТОВАЯ ОПТИКА
31.1. Тепловое излучения и люминесценция. Основные понятия.
Тепловым излучением называется испускание телами электромагнитных волн за счёт их внутренней энергии. Все остальные виды свечения - люминесценция.
 Рассмотрим излучение, которое находится в равновесии с излучающим телом. Для этого представим тело, окружённое идеально отражающей оболочкой.
Рассмотрим излучение, которое находится в равновесии с излучающим телом. Для этого представим тело, окружённое идеально отражающей оболочкой.
Воздух из полости удалён. Отражённое оболочкой излучение частично поглощается телом, и между телом и излучением в пространстве между телом и оболочкой происходит непрерывный обмен энергией. Если распределение энергии между телом и излучением остаётся неизменным для каждой длины волны, то тело и излучение находятся в равновесии.
Экспериментально установлено, что в равновесии с излучающим телом может находиться только тепловое излучение. Эта его особенность обусловлена тем, что интенсивность теплового излучения растёт с ростом температуры и уменьшается в обратном случае.
К равновесным процессам и состояниям применимы законы термодинамики. Поэтому тепловое излучение должно подчиняться некоторым общим закономерностям, вытекающим из принципов термодинамики, которые мы должны рассмотреть. Однако, чтобы сформулировать эти закономерности, необходимо ввести ряд понятий.
Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям во всём диапазоне частот, называется энергетической светимостью R тела. Энергетическая светимость определяется температурой 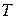 излучающего тела:
излучающего тела:
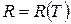 (31.1)
(31.1)
Экспериментально установлено, что излучение тела распределено по спектру неравномерно. Для того, чтобы охарактеризовать это распределение используют функцию частоты и температуры излучающего тела  , которую будем называть испускательной способностью тела. Если в интервале частот от
, которую будем называть испускательной способностью тела. Если в интервале частот от 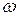 до
до 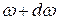 с единицы поверхности излучается поток энергии
с единицы поверхности излучается поток энергии  , то величина
, то величина 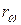 , равная
, равная
 (31.2)
(31.2)
называется испускательной способностью тела. Эту величину можно также назвать спектральной плотностью энергетической светимости. Вполне очевидно, что эта функция должна, как и  , сильно зависеть от температуры. Поэтому в дальнейшем будем использовать обозначение
, сильно зависеть от температуры. Поэтому в дальнейшем будем использовать обозначение 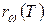
Распределение излучения по спектру можно характеризовать либо зависимостью от частоты излучения, исходящего от тела,  , либо зависимостью от длины волны излучения
, либо зависимостью от длины волны излучения 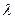 . Исторически сложилось так, что при теоретических исследованиях рассматриваются зависимости от частоты, а экспериментально – от длины волны. При сопоставлении этих зависимостей необходимо учитывать связь между соответствующими функциями.
. Исторически сложилось так, что при теоретических исследованиях рассматриваются зависимости от частоты, а экспериментально – от длины волны. При сопоставлении этих зависимостей необходимо учитывать связь между соответствующими функциями.
Участку 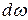 в спектре излучения некоторого тела соответствует интервал длин волн
в спектре излучения некоторого тела соответствует интервал длин волн 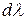 . Поскольку речь идет об одном и том же участке в спектре излучения, между
. Поскольку речь идет об одном и том же участке в спектре излучения, между 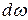 и
и 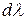 должна быть связь. Действительно, из соотношения
должна быть связь. Действительно, из соотношения
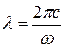 (31.2)
(31.2)
следует, что
 (31.3)
(31.3)
Минус в этом соотношении отражает тот факт, что росту частоты соответствует уменьшение длины волны и приращения 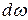 и
и 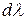 имеют разные знаки. Если нас интересует соотношение между модулями, то минус можно просто отбросить.
имеют разные знаки. Если нас интересует соотношение между модулями, то минус можно просто отбросить.
Соответственно распределение излучения по спектру можно характеризовать функцией длины волны  .
.
 (31.4)
(31.4)
Если 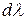 и
и 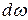 соответствует одному и тому же участку спектра излучения некоторого тела при данной температуре, то потоки излучения
соответствует одному и тому же участку спектра излучения некоторого тела при данной температуре, то потоки излучения  и
и  должны быть равны:
должны быть равны:
 (31.5)
(31.5)
Подставив вместо 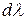 его значение (31.3), получим
его значение (31.3), получим
 . (31.6)
. (31.6)
Поэтому связь  и
и  можно представить в виде:
можно представить в виде:
 . (31.7)
. (31.7)
Излучение, падающее на тело, частично им поглощается, а частично отражается. Степень поглощения телом падающего излучения зависит от его спектрального состава и состояния тела, в частности его температуры. Пусть в интервале частот d  падает поток лучистой энергии
падает поток лучистой энергии  , и часть
, и часть  этого потока поглощается телом. Величина
этого потока поглощается телом. Величина
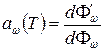 . (31.8)
. (31.8)
называется поглощательной способностьютела. В соответствии с определением 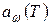 есть безразмерная величина и
есть безразмерная величина и 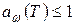 .
.
Тело, для которого  называется абсолютно чёрным. Необходимо подчеркнуть, что определение абсолютно чёрного телане подразумевает, что это тело ничего не излучает (К сожалению, это представление является распространенным заблуждением). Наоборот, именно абсолютно чёрное тело наиболее эффективно отдает энергию за счет теплового излучения. И по этой причине, например, поверхность радиаторов элементов электронной аппаратуры для большей их эффективности «чернят».
называется абсолютно чёрным. Необходимо подчеркнуть, что определение абсолютно чёрного телане подразумевает, что это тело ничего не излучает (К сожалению, это представление является распространенным заблуждением). Наоборот, именно абсолютно чёрное тело наиболее эффективно отдает энергию за счет теплового излучения. И по этой причине, например, поверхность радиаторов элементов электронной аппаратуры для большей их эффективности «чернят».
Отметим, что человек, одетый в белую одежду, в инфракрасные приборы ночного видения будет менее заметным, чем одетый в темную одежду (при условии, что не используется инфракрасный фонарь).
Если  , то тело называют серым.
, то тело называют серым.
 Тел с абсолютно чёрной поверхностью, как и других идеальных объектов в природе не бывает. Например, поверхность, на которую нанесена сажа, близка к абсолютно черной только в ограниченном частотном диапазоне. Однако легко создать устройство, участок поверхности которого будет сколь угодно близок к абсолютно черному телу. Действительно, если внутри тела создать полость, поверхность которой покрыть той же сажей, то небольшое отверстие ведущее внутрь полости для стороннего наблюдателя будет вполне соответствовать по свойствам абсолютно черному телу. Любой луч, упавший на поверхность, отверстия практически полностью поглощается внутри полости. Вероятность выхода луча через отверстие во вне полости исчезающее мала, а интенсивность при каждом отражении внутри уменьшается во много раз.
Тел с абсолютно чёрной поверхностью, как и других идеальных объектов в природе не бывает. Например, поверхность, на которую нанесена сажа, близка к абсолютно черной только в ограниченном частотном диапазоне. Однако легко создать устройство, участок поверхности которого будет сколь угодно близок к абсолютно черному телу. Действительно, если внутри тела создать полость, поверхность которой покрыть той же сажей, то небольшое отверстие ведущее внутрь полости для стороннего наблюдателя будет вполне соответствовать по свойствам абсолютно черному телу. Любой луч, упавший на поверхность, отверстия практически полностью поглощается внутри полости. Вероятность выхода луча через отверстие во вне полости исчезающее мала, а интенсивность при каждом отражении внутри уменьшается во много раз.
Закон Кирхофа
 Рассмотрим систему, состоящую из нескольких тел, окруженных оболочкой, поддерживаемой при постоянной температуре
Рассмотрим систему, состоящую из нескольких тел, окруженных оболочкой, поддерживаемой при постоянной температуре 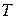 в условиях, когда тела могут обмениваться энергией только за счет излучения и поглощения электромагнитных волн. (отдаленно напоминающей эту ситуацию можно считать продукты, помещенные в холодильник, если забыть об обмене энергией за счет конвекции). Очевидно, что спустя некоторое время все тела системы будут иметь одинаковую температуру, независимо от их природы. Однако испускательные
в условиях, когда тела могут обмениваться энергией только за счет излучения и поглощения электромагнитных волн. (отдаленно напоминающей эту ситуацию можно считать продукты, помещенные в холодильник, если забыть об обмене энергией за счет конвекции). Очевидно, что спустя некоторое время все тела системы будут иметь одинаковую температуру, независимо от их природы. Однако испускательные 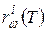 и поглощательные
и поглощательные  способности тел системы различны. Поэтому тело больше поглощающее энергию должно больше ее и излучать, чтобы температура тела оставалась равной
способности тел системы различны. Поэтому тело больше поглощающее энергию должно больше ее и излучать, чтобы температура тела оставалась равной 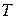 . Это соотношение поглощательной и испускательной способностей тела является отражает закона Кирхгофа, согласно которому отношение испускательной и поглощательной способности тел является для всех тел универсальной функцией частоты (длины волны) и температуры:
. Это соотношение поглощательной и испускательной способностей тела является отражает закона Кирхгофа, согласно которому отношение испускательной и поглощательной способности тел является для всех тел универсальной функцией частоты (длины волны) и температуры:
 . (31.9)
. (31.9)
Для абсолютного черного тела  , а значит, универсальная функция
, а значит, универсальная функция  в законе Кирхгофа имеет смысл испускательной способности абсолютно черного тела.
в законе Кирхгофа имеет смысл испускательной способности абсолютно черного тела.
Аналогично соотношению (31.7) универсальная функция длины волны и температуры 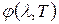 в законе Кирхгофа при рассмотрении зависимостей от длины волны связана с
в законе Кирхгофа при рассмотрении зависимостей от длины волны связана с 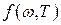 соотношением:
соотношением:
 . (31.10)
. (31.10)
 В результате экспериментального исследования излучения исходящего из отверстия в полость, близкого к излучению абсолютно черного тела, был установлен вид
В результате экспериментального исследования излучения исходящего из отверстия в полость, близкого к излучению абсолютно черного тела, был установлен вид 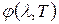 , приблизительно показанный на рисунке 31.4. Графики соответствуют трем температурам:
, приблизительно показанный на рисунке 31.4. Графики соответствуют трем температурам:  >
>  >
> 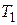 . Очевидно, что с ростом температуры существенно увеличивается энергетическая светимость тела, которой соответствует площадь графика под зависимостью
. Очевидно, что с ростом температуры существенно увеличивается энергетическая светимость тела, которой соответствует площадь графика под зависимостью 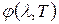 . Кроме того, длина волны
. Кроме того, длина волны  , на которую приходится максимум излучающей способности, уменьшается с ростом температуры. Вин установил закономерность, согласно которой
, на которую приходится максимум излучающей способности, уменьшается с ростом температуры. Вин установил закономерность, согласно которой
 . (31.11)
. (31.11)
Эту особенность спектра излучения абсолютно черного тела называют законом смещения Вина (речь идет о смещении  при изменении температуры).
при изменении температуры).
Стефан, на основе анализа экспериментаьльных данных по светимости различных тел, пришел к выводу, что энергетическая светимость всех тел пропорциональна четвертой степени температуры. Однако Больцман доказал, что такое соотношение справедливо только для абсолютно черных тел. Поэтому утверждение о том, что
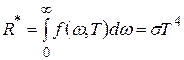

Дата добавления: 2021-01-11; просмотров: 579;











