Расчет цилиндрической передачи
1.Выбор варианта термообработки зубчатых колес.
Принимаем вариант термообработки (т.о.) I (см. табл. 1П.6 приложения 1П): т.о. шестерни - улучшение, твердость поверхности 269...302 НВ; т.о. колеса - улучшение, твердость поверхности 235...262 НВ; марки сталей одинаковы для шестерни и колеса: 40Х;
2.Предварительное определение допускаемого контактного напряжения при проектном расчете на сопротивление контактной усталости. Средняя твердость H поверхности зубьев:
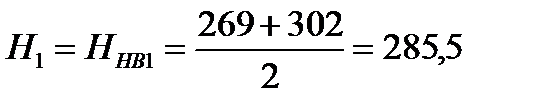 НВ;
НВ;
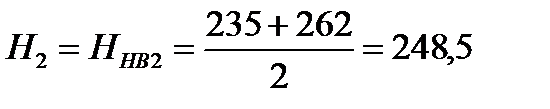 НВ;
НВ;
Предел контактной выносливости поверхности зубьев σH lim, соответствующий базовому числу циклов напряжений (см. табл. 1П.9 приложения 1П) для т.о. улучшение:
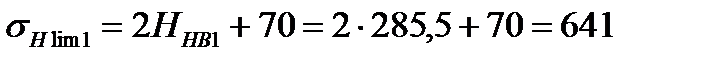 МПа;
МПа;
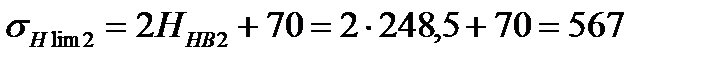 МПа;
МПа;
Расчетный коэффициент SН (табл. 1П.9 приложения 1П) для т.о. улучшение:
SН1= SН2=1,1.
Базовое число циклов напряжений NН lim:
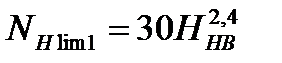
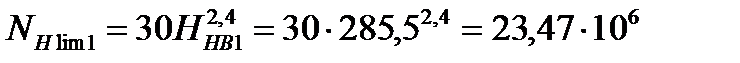 ;
;
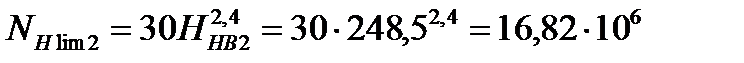 ;
;
Эквивалентное число циклов напряжений NНE за расчетный срок службы передачи Lh=10000 часов:
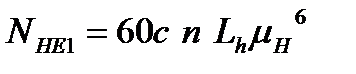
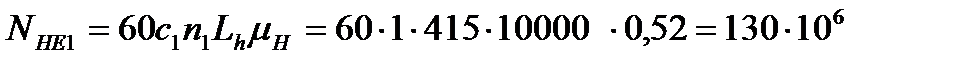 ;
;
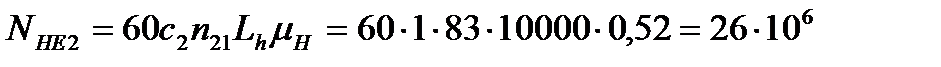 ;
;
где с1, и с2 -число зацеплений за один оборот соответственно зуба шестерни и зуба колеса; с1=1; с2 =1; µH=0,52- согласно графика нагружения.
Определяем коэффициенты долговечности ZN1и ZN2. Так как NНE1>NНlim1, тогда
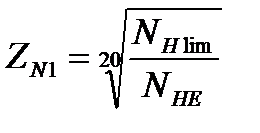
 .
.
Так как NНE2>NНlim2, тогда
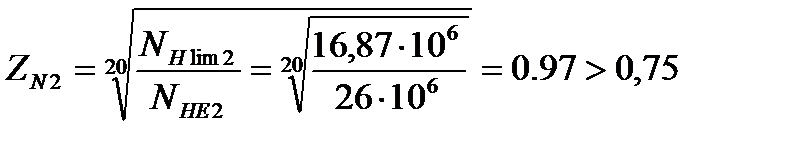 .
.
Предварительная величина допускаемого контактного напряжения при расчете передачи на сопротивление контактной усталости:
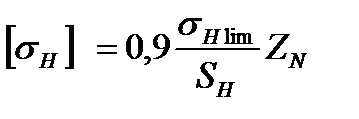
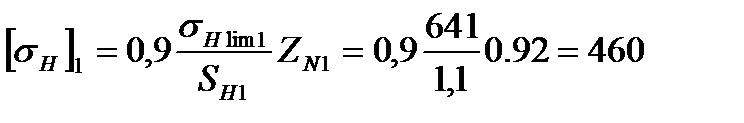 МПа;
МПа;
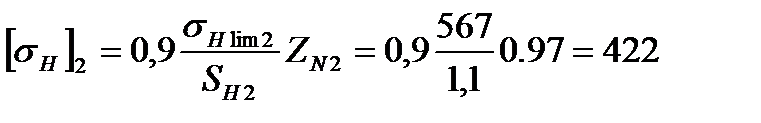 МПа;
МПа;
В качестве расчетного допускаемого контактного напряжения [σн] при расчете прямозубой цилиндрической передачи на контактную усталость принимается минимальное напряжение из [σн]1 и [σн]2.
В нашем примере [σн]= [σн]1=422 МПа.
3. Определение межосевого расстоянии. По табл. 1П.11 приложения 1П выберем коэффициент ψba. В данной таблице в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев указывается диапазон рекомендуемых значений ψba. В указанном диапазоне ψba рекомендуется принимать из ряда стандартных чисел: 0,15; 0,2; 0,25; 0,315; 0,4 и 0,5. Данных рекомендаций допускается не придерживаться при проектировании нестандартных редукторов.
В нашем примере шестерня рассчитываемой ступени расположена симметрично относительно опор, а колесо - симметрично (см. схему привода). По табл. 1П.11 приложения 1П при HB1<350 и HB2<350 принимаем из диапазона ψba = 0,3...0,5 расчетное значение ψba =0,5 и значение ψbdmax=1,4.
Тогда коэффициент ψba (предварительно):
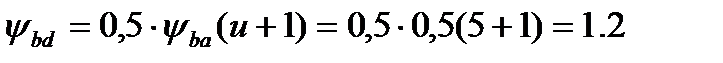
По табл. 1П.12 приложения 1П при НВ1<350 и НВ2 <350 для кривой IV (редуктор соосный) принимаем коэффициент КHβ = 1,1.
Приняв для прямозубой цилиндрической передачи вспомогательный коэффициент Кα= 495, определим предварительно межосевое расстояние а'w :
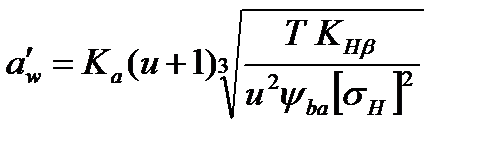 (2.18)
(2.18)
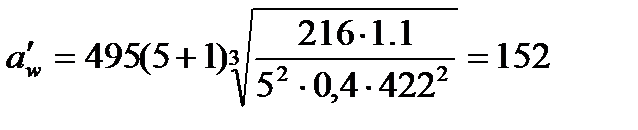 мм.
мм.
По табл. 1П. 13 приложения 1П принимаем ближайшее стандартное значение аw = 160 мм.
4. Определение модуля передачи.
m 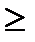 Km·T2(u+1)/(u·aw·b2· [σ]F),
Km·T2(u+1)/(u·aw·b2· [σ]F),
m > 6,6·216·(5+1)/(5·160·64·199) = 0,84 мм,
где Km = 6.6 – для прямозубых колес,
принимаем по ГОСТ 9563-60 m = 2 мм.
5. Определение чисел зубьев шестерни и колеса. Суммарное число зубьев
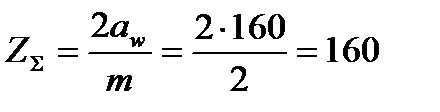
Число зубьев шестерни
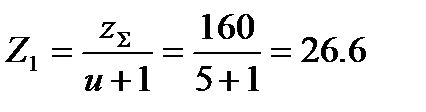 принимаем Z1=27.
принимаем Z1=27.
Число зубьев колеса
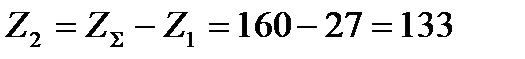 .
.
6. Определение фактического передаточного числа ступени.
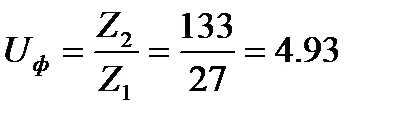
Отклонение Uф от U:
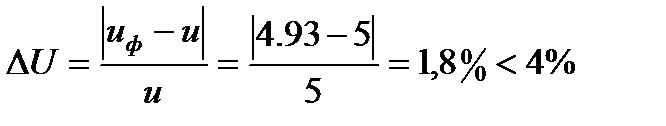 .
.
7. Определение основных размеров шестерни и колеса. Диаметры делительные:
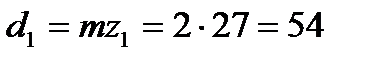 мм;
мм;
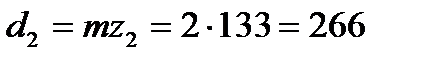 мм.
мм.
Проверка:
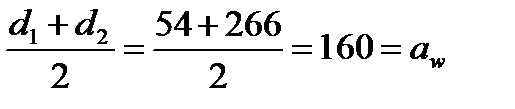 мм.
мм.
Примем коэффициент высоты головки зуба ha* = 1 и коэффициент радиального зазора с*= 0,25. Тогда, диаметры окружностей вершин da и впадин df зубьев при высотной модификации:
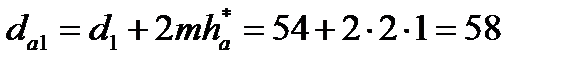 мм;
мм;
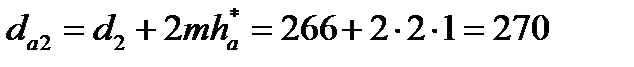 мм;
мм;
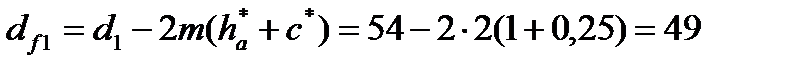 мм;
мм;
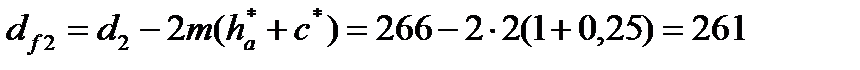 мм.
мм.
Ширина венца колеса
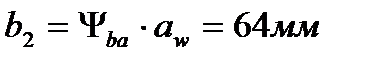 мм,
мм,
Ширина венца шестерни
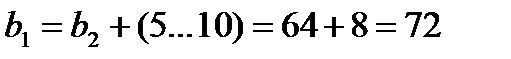 мм.
мм.
Уточняем коэффициент ψbd:
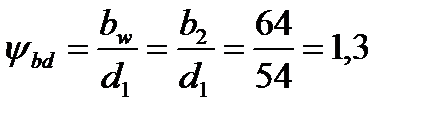 , что меньше ψbdmax =1,4
, что меньше ψbdmax =1,4
Проверочный расчет
8. Проверка пригодности заготовок зубчатых колес и выбор материала
для их изготовления. Диаметр заготовки шестерни
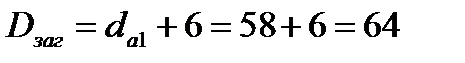 мм.
мм.
Условие пригодности заготовки шестерни
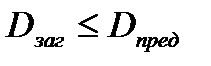 ,
,
Где Dпред -см. табл.1П.7 приложения 1П. Для стали 40Х при т.о. улучшение для твердости поверхности 235...262 НВ Dпред=200 мм. Таким образом, для изготовления шестерни принимаем сталь 40Х. Выберем материал для изготовления колеса. Для этого определим толщину заготовки диска колеса Сзаг и толщину заготовки обода Sзаг:
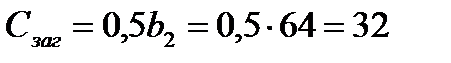 мм;
мм;
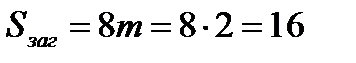 мм.
мм.
Наибольшую из величин Сзаг и Sзаг сравниваем для той же марки стали, что и для шестерни (т.е. 40Х) по табл. 1П.7 приложения 1П при т.о. улучшение для твердости поверхности 235...262 НВ с Sпред =125 мм. Условие Сзаг =56< Sпред =125 мм выполняется. Таким образом, для изготовления колеса также подходит сталь 40Х
9. Определение степени точности передачи. Окружная скорость υ (м/с)
шестерни или колеса в полюсе зацепления одинакова и может быть определена:
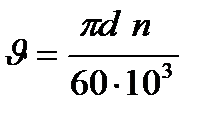 (2.22)
(2.22)
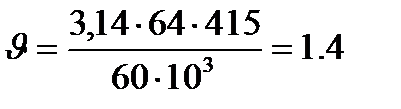 м/с.
м/с.
По табл. 1П.15 приложения 1П, исходя из υ=1,4 м/с для косозубых цилиндрических передач выбираем 9-ю степень точности, при которой допускается окружная скорость зубчатых колес до 2 м/с.
10. Уточнение допускаемого контактного напряжения при проверочном расчете на сопротивление контактной усталости. На основании рекомендаций, изложенных в п. 2.1, принимаем параметр шероховатости Rа = 3,2 мкм и коэффициент ZR =0,9. Коэффициент ZV =1, т.к. υ<5 м/с.
Тогда по формуле:
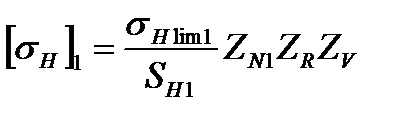 (2.23)
(2.23)
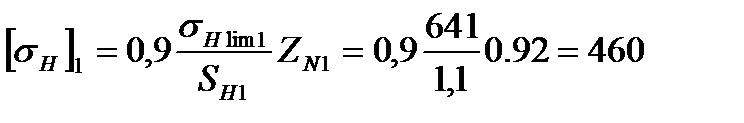 МПа;
МПа;
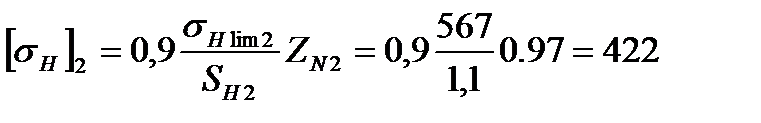 МПа;
МПа;
Таким образом, уточненные величины [σн]1 и [σн]2 остались такими же , как и при предварительном расчете ввиду того, что произведение ZR ZV оказалось равным 0,9.
Следовательно, уточненная величина расчетного допускаемого контактного напряжения [σн] будет такой же, как и при предварительном расчете, т.е. [σн]=422 МПа (см. п. 2).
11. Определение сил, действующих в косозубом зацеплении. Окружная сила Ft на делительном цилиндре
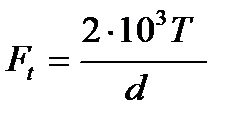 (2.24)
(2.24)
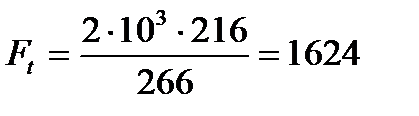 Н
Н
При этом для шестерни и колеса:
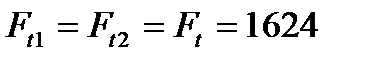 Н.
Н.
Радиальная сила Fr:
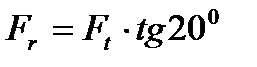 (2.25)
(2.25)
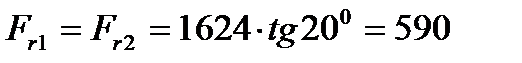 Н.
Н.
12.Определение коэффициента нагрузки Кн. При расчете на сопротивление контактной усталости
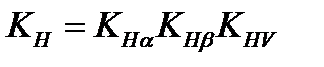
Коэффициент КНа = 1 -для косозубых передач.
Коэффициент KHβ уточняем по той же кривой IV при HB1<350 и HB2<350 (см. табл. 1П.12 приложения 1П), что и при предварительном расчете в п.3, в зависимости от уточненной в п.7 величины ψbd=0,98. При этом коэффициент Kнβ практически не изменился: KHβ=1,05.
По табл. 1П.17 приложения 1П коэффициент δН=0,06 при HB1<350 и HB2<350 .
По табл. 1П.18 приложения 1П коэффициент g0= 7,3 (при m=2 мм и 9-й степени точности).
Тогда динамическая добавка
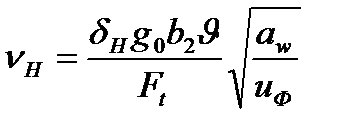 (2.26)
(2.26)
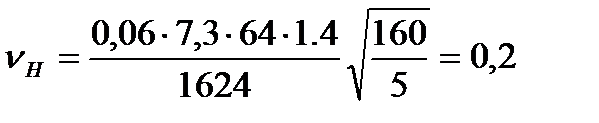
Коэффициент KHV:
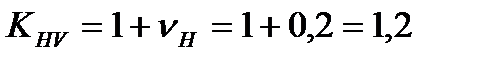 .
.
Окончательно
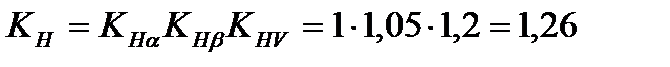 .
.
13. Проверочный расчет передачи на сопротивление контактной усталости. Для стальных зубчатых колес коэффициент ZH, учитывающий механические свойства материалов сопряженных зубьев: ZЕ =190 МПа1/2.
ч определяют в зависимости от от коэффициента осевого перекрытия 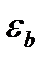 .
.
Коэффициент торцового перекрытия зубьев для косозубой передачи приближенно можно определить по формуле
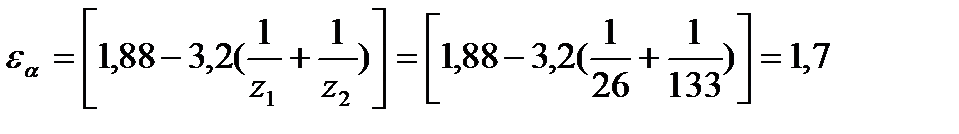
Коэффициент, учитывающий суммарную длину контактных линий, для косозубой передачи, так как 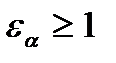 , то:
, то: 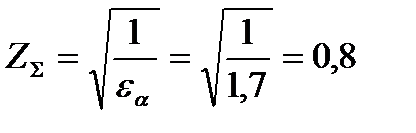 .
.
Расчетное значение контактного напряжения
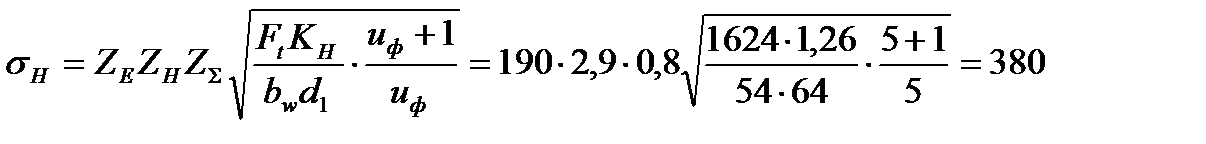 МПа
МПа
Сопротивление контактной усталости обеспечивается, так как выполняется условие: σн=380 МПа < [σн]=422 МПа.
0,9 [σн] 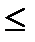 σн
σн 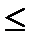 1,05 [σн]
1,05 [σн]
Недогрузка (380 – 422)100/422 = 9,9% допустимо 10%.
14. Определение допускаемого напряжения изгиба при расчете зубьев на сопротивление усталости при изгибе. По табл. 1П.9 приложения 1П принимаем:
а) для шестерни (т. о. улучшение + закалка ТВЧ), при m=3 мм.
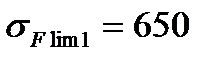 МПа;
МПа; 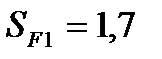 ;
;
б) для колеса (т. о. улучшение)
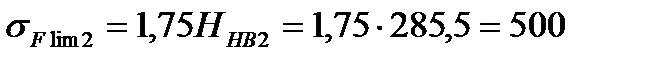 МПа, (см. п.2),
МПа, (см. п.2), 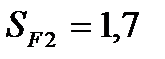
Принимаем величины qF, YNmax:
а) для шестерни qF = 9; YNmaх=2,5 при H1>350 МПа;
б) для колеса qF = 6; YNmaх=4 при H1<350 МПа;
Эквивалентное число циклов напряжений NFE за расчетный срок службы Lh =10*103 часов, где с, и с2 - см. п. 2.:
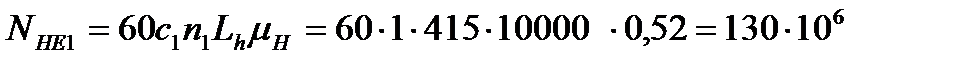 ;
;
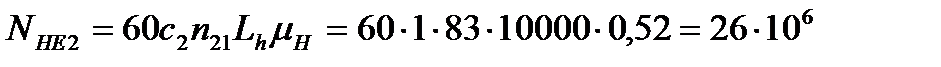 ;
;
На основании рекомендаций, изложенных в п. 2.1,определяем коэффициенты долговечности YN1 и YN2.
Для шестерни при NFE> NFlim1 принимается YN1 =1.
Для колеса при при NFE> NFlim1 принимается YN1 =1.
Тогда допускаемое напряжение изгиба:
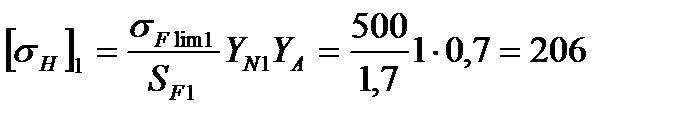 МПа;
МПа;
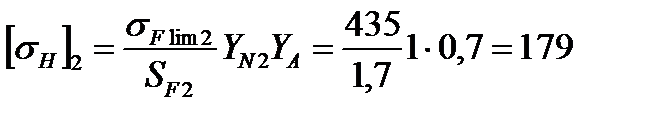 МПа.
МПа.
15. Определение коэффициента нагрузки КF. Коэффициент нагрузки при расчете зубьев на сопротивление усталости при изгибе:
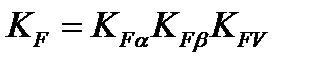 (2.27)
(2.27)
Коэффициент КFа = 1 -для косозубых передач.
Коэффициент KFβ принимаем по табл. 1П.12 приложения 1П при HB1<350 и HB2<350 при ψbd=0,98 (кривая V): KFβ =1,1.
Коэффициент δF ,учитывающий влияние вида зубчатой передачи и модификации профиля зубьев: δF =0,16 .
Коэффициент g0= 7,3- см. п.12.
Тогда динамическая добавка
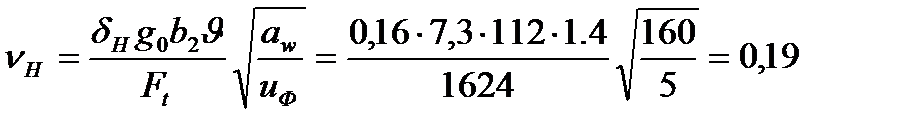
Коэффициент KHV:
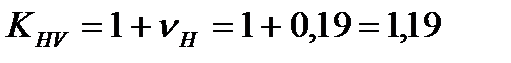 .
.
Окончательно
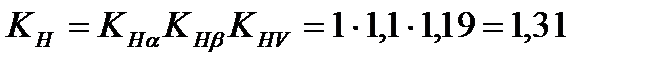 .
.
16 Проверочный расчет зубьев на сопротивление усталости при изгибе.
Коэффициент YFS, учитывающий форму зуба и концентрацию напряжений:
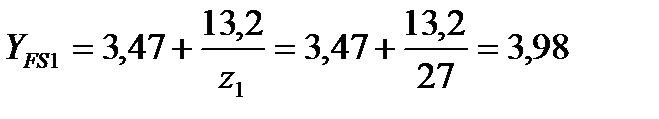 ;
;
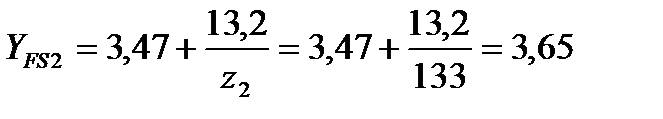 .
.
Тогда расчетное напряжение изгиба σF:
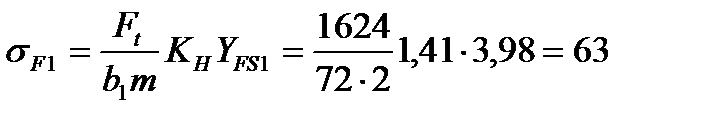 МПа;
МПа;
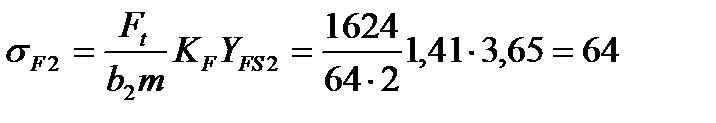 МПа.
МПа.
Сопротивление усталости при изгибе обеспечивается, так как выполняются условия:
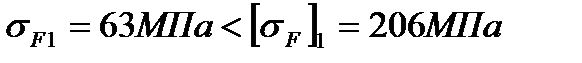
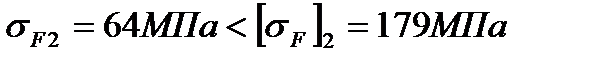
Отмечаем, что для данного варианта термообработки основным критерием работоспособности передачи является сопротивление контактной усталости, а не усталости при изгибе.
17. Проверочный расчет передачи на контактную прочность при действии пиковой нагрузки (при кратковременной перегрузке). Цель данного расчета - проверка статической прочности зубьев при действии пиковой нагрузки (при кратковременной перегрузке), не учтенной при расчете на сопротивление контактной усталости. По табл. 1П.9 приложения 1П предельно допускаемое контактное напряжение 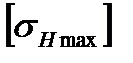 :
:
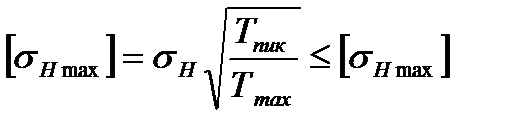 МПа;
МПа;
где - 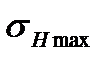 - максимальное контактное напряжение,
- максимальное контактное напряжение, 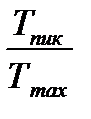 - кратковременная перегрузка.
- кратковременная перегрузка.
Определяем для шестерни и колеса 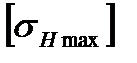 согласно таблице 1П.9 приложения 1П.:
согласно таблице 1П.9 приложения 1П.:
а) для шестерни: 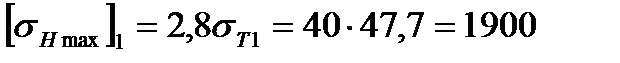 МПа.
МПа.
б) для колеса 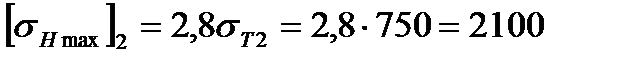 МПа.
МПа.
В качестве расчётной принимаем наименьшую величину 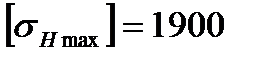 МПа.
МПа.
Тогда для рассчитываемой ступени:
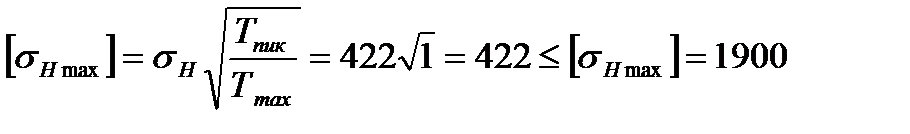 МПа.
МПа.
18. Проверочный расчет передачи при изгибе пиковой нагрузкой (при кратковременной перегрузке). Цель данного расчета - проверка статической прочности зубьев при действии пиковой нагрузки (при кратковременной перегрузке), не учтенной при расчете зубьев на сопротивление усталости при изгибе.
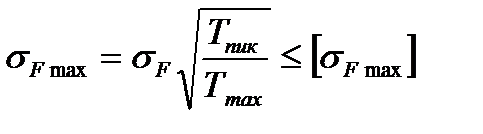
где 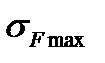 - максимальное напряжение изгиба при кратковременной перегрузки.
- максимальное напряжение изгиба при кратковременной перегрузки.
По табл. 1П.9 приложения 1П предельно допускаемое напряжение изгиба
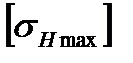 :
:
а) для шестерни: 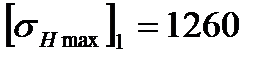 Мпа;
Мпа;
б) для колеса: 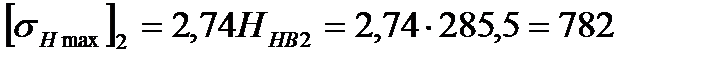 Мпа,
Мпа,
где 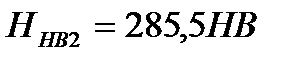 (см. п. 2).
(см. п. 2).
Ранее мы получили 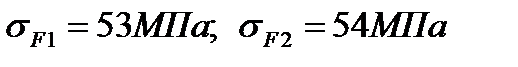 (см. п. 16).
(см. п. 16).
Тогда для рассчитываемой ступени:
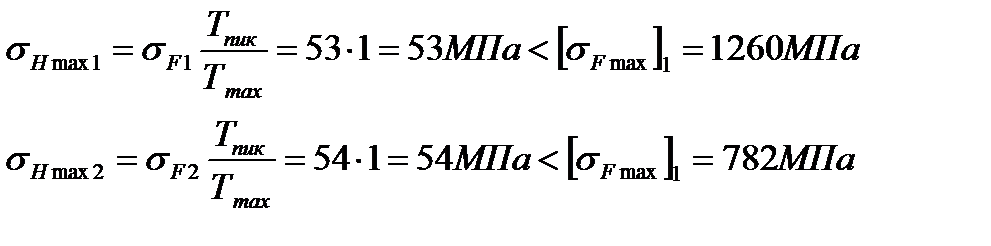
Дата добавления: 2019-05-21; просмотров: 1541;











