Схема круговой кривой
Для расчета закругления на местности теодолита измеряют угол β, для того чтобы вычислить угол поворота трассы φ=180º–β (φ–угол между первоначальным и последующим направлением трассы)
Радиус закругления R выбирают в соответствии с условиями техники безопасности эксплуатации сооружения и рельефа. По φ и R вычисляют основные элементы круговой кривой.
Тангенс (Т) – расстояние от вершины угла (ВУ) до начало кривой (НК) или конца кривой (КК):
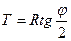
Кривая (К) – длина дуги окружности с радиусом R от НК до КК:
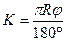
Биссектриса (Б) – расстояние от ВУ до середины кривой (СК):
Б 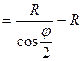
Домер (Д) – разность путей по ломаной линии и дуге:
Д=2Т–К
За концом кривой все пикеты смещаются вперед на Д.
Для того чтобы разбить круговую кривую на местности достаточно закрепить ее основные точки: начало, середину и конец.
Для того чтобы закрепить НК и КК от ВУ по оси трассы откладывают Т. Для того чтобы закрепить СК, при помощи теодолита откладывают угол β/2 и в этом направлении откладывают Б.
Пикетажное значение НК и КК вычисляют по формулам:
НК=ВУ–Т
КК=НК+К
Контроль: КК=ВУ+Т–Д
При больших R не достаточно только закрепить НК, СК, КК. В этом случае пользуются детальной разбивкой круговой кривой, которая выполняется, например, способом прямоугольных координат, продолженных хорд и т.д.
Дальше приступают к нивелированию трассы, которое начинают с привязки трассы к реперу ГВС. Привязка заключается в проложении нивелирного хода о репера до начала трассы (ПК0). Далее нивелируют пикеты, «плюсовые» точки, поперечники, главные точки кривых. Нивелирование выполняется геометрическим способом «из середины», причем пикеты нивелируют как связующие точки (по двум сторонам реек), а остальные как промежуточные (по черной стороне). Заканчивается нивелирование привязкой трассы к реперу высотной сети.
Дата добавления: 2016-09-26; просмотров: 2574;











