Цифровые синтезаторы частоты с косвенным синтезом (ФАПЧ).

Метод синтеза частоты называют косвенным, если выходное колебание синтезатора частоты формируется отдельным перестраиваемым генератором, частота которого автоматически подстраивается специальной схемой по эталонному колебанию другого генератора, как правило, высокостабильного. В результате в установившемся режиме частота выходного колебания находится в дробно-кратном соотношении с частотой колебания эталонного генератора. В качестве схемы управления перестраиваемого генератора используют ту или иную модификацию системы фазовой автоматической подстройки частоты (ФАПЧ или PLL), при этом в установившемся синхронном режиме и начальная фаза выходного колебания синтезатора зависит от начальной фазы эталонного колебания.

Рассмотрим структуру простейшего однопетлевого синтезатора частоты с косвенным методом синтеза (рис.7.4.1). Принцип работы этой схемы хорошо известен [17-19]: частотно-фазовый детектор (ЧФД) подстраивает частоту генератора, управляемого напряжением (ГУН) до тех пор, пока не буде выполнено равенство

F₀ / M = F_вых / N, тогда F_вых = (F₀ / M)·N.

Очевидно, что частота выходного колебания зависит от коэффициентов деления делителя опорной частоты М и ДПКД - делителя частоты с переменным коэффициентом деления N, установленного в цепи обратной связи. Петлевой фильтр обеспечивает заданные динамические характеристики (время установления и характер переходного процесса) и устойчивость петли ФАПЧ.

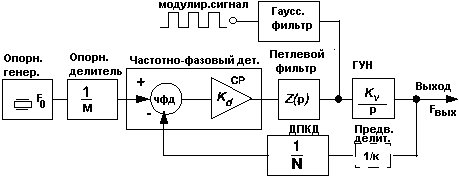
Рис.7.4.1.

Здесь (F₀ / M) имеет смысл шага перестройки по частоте синтезатора. Рассмотрим возможные последствия уменьшения шага перестройки частоты синтезатора.

1) Поскольку частота (F₀ / M) является частотой сравнения ЧФД, от ее величины зависят параметры петлевого фильтра. Следовательно, при уменьшении шага перестройки частоты синтезатора увеличивается длительность переходных процессов, т.е. фактически, время перестройки синтезатора с одной частоты на другую. Как правило, длительность переходного процесса может составлять 30…300 интервалов частоты сравнения ЧФД (в зависимости от параметров петлевого фильтра и выходного каскада самого ЧФД).

2) В соответствии с приведенной выше формулой для выходной частоты синтезатора, при уменьшении частоты сравнения (F₀ / M) требуется соответствующее увеличение коэффициента деления частоты N, что приводит к пропорциональному увеличению фазовых шумов в выходном колебании синтезатора. Данный эффект обусловлен тем, что по существу петля ФАПЧ умножает в N раз не просто частоту сравнения, но полную фазу колебания, поступающего на вход эталонной частоты фазового (частотно-фазового) дискриминатора, в том числе и шумовую составляющую полной фазы. Как будет показано ниже, по отношению к «внешним» шумам, проникающим в петлю ФАПЧ с «опорного» входа дискриминатора, она ведет себя как ФНЧ, т.е. беспрепятственно пропускает модулирующее шумовое воздействие с этого входа на ГУН, дополнительно усиливая эти шумы в N раз.

В качестве детектора ошибки по фазе в данной схеме может применяться как фазовый детектор (дискриминатор), так и частотно-фазовый детектор. Преимуществом последнего является его чувствительность к величине и знаку рассогласования частоты в режиме отсутствия синхронизации в петле ФАПЧ, благодаря чему полоса захвата в схеме с ЧФД становится равной полосе удержания. Подробнее работа ЧФД рассмотрена в параграфе 7.7, здесь же уместно отметить, что выходной каскад ЧФД в современных интегральных схемах ФАПЧ-синтезаторов строится как преобразователь с накачкой заряда - «зарядовый насос» (charge pump – CP). Применение СР, как каскада, имеющего токовый выход, позволяет включать в петлю ФАПЧ интегрирующее звено (в одном из вариантов ПИФ – пропорционально-интегрирующего фильтра), тем самым придавая петле ФАПЧ свойство астатизма.

Выходной каскад типа СР вырабатывает импульсы тока фиксированной амплитуды, длительность и полярность которых зависит от величины и знака рассогласования фазы в петле ФАПЧ (см. параграф 7.7). Именно от амплитуды импульсов выходного тока СР во многом зависит длительность переходного процесса петли ФАПЧ при смене частоты в пределах полосы удержания или при захвате частоты. В связи с этим выходной ток СР во многих ИМС косвенных синтезаторов делают переключаемым: при смене частоты для ускорения переходного процесса заранее включают режим максимального выходного тока СР, а после окончания переходного процесса для обеспечения экономичности снижают выходной ток СР в несколько раз. Например, в ИМС TSA6057 (см. параграф 8.3) максимальный выходной ток СР составляет 5 мА, а минимальный 0,5 мА.

Преобразователь с накачкой заряда является импульсной схемой, благодаря чему он может оказаться источником нежелательных спектральных составляющих в спектре выходного колебания; эти составляющие легко «узнать», поскольку они располагаются на частотах, отстоящих от частоты основного колебания ГУН на величину, кратную частоте сравнения ЧФД. Так, на рис. 7.4.2 [17] в спектре колебания синтезатора, настроенного на 1880 МГц, видны «следы» частоты сравнения ЧФД 200 кГц.

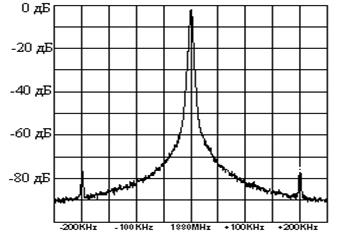
Рис. 7.4.2.

В режиме удержания частоты после окончания всех переходных процессов в петле ФАПЧ устанавливается состояние равновесия, в котором оба входных колебания ЧФД имеют строго одинаковую частоту (а в схемах ФАПЧ со свойством астатизма – и одинаковую фазу, т.е. в пределах полосы удержания в стационарном режиме ошибка по фазе отсутствует), следовательно, выходное управляющее воздействие на выходе ЧФД должно отсутствовать. В «идеальной» схеме синтезатора частоты, т.е. построенной из элементов, не имеющих утечек по току в цепи выход ЧФД – петлевой фильтр – управляющий вход ГУН, так и будет, но реально существуют утечки по току в ключах каскада СР самого ЧФД, в конденсаторах петлевого фильтра, в цепи смещения варикапа ГУН. Даже наноамперные токи утечки приводят к тому, что ЧФД будет вынужден все время «подкачивать» короткими импульсами тока петлевой фильтр и входную цепь ГУН, как это показано на рис. 7.4.3 [17], что и приводит к проникновению нежелательных составляющих в спектр колебания ГУН.

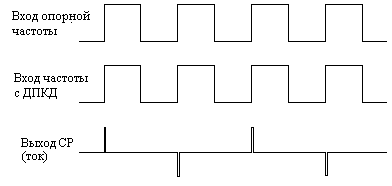
Рис. 7.4.3

Периодическая модуляция частоты в такой схеме однопетлевого синтезатора (этот способ модуляции применяется, например, в цифровых передатчиках системы DECT на частоте 1.9 ГГц) осуществляется после достижения установившегося значения средней частоты ГУН. Для этого петля ФАПЧ размыкается путем установления выхода ЧФД в третье состояние, затем через гауссовский фильтр на ГУН подается пачка модулирующих частоту импульсов, после чего петля ФАПЧ снова замыкается и производится подстройка среднего значения частоты. Разумеется, за то время, пока ЧФД не управляет частотой ГУН, последняя «дрейфует», отклоняясь от номинального значения. Величина этого отклонения зависит от уже упомянутых в предыдущем абзаце утечек по току в ключах выходного каскада ЧФД, в конденсаторах петлевого фильтра, в цепи смещения варикапа ГУН, а также от других дестабилизирующих факторов (наводок, пульсаций в цепи питания, затягивания частоты ГУН, и пр., см. параграф 8.1). Тем не менее, размыкать петлю ФАПЧ на время прохождения пакета модулирующих импульсов необходимо, так как вводимое после ЧФД (рис.7.4.1) модулирующее воздействие воспринимается петлей ФАПЧ как «внутренняя» помеха. Ниже будет показано, что по отношению к «внутренним» помехам замкнутая петля ФАПЧ ведет себя как ФВЧ, т.е. пытается компенсировать такое модулирующее воздействие, сводя результат модуляции к нулю.

Итак, рассмотрим в упрощенном изложении вопрос о влиянии помех и шумов на спектр выходного колебания простой системы ФАПЧ (рис. 7.4.1) [17].

Условимся, что для малых (шумовых) возмущений фазы колебания петлю ФАПЧ можно рассматривать как линейную непрерывную систему автоматического регулирования (САР), что дает возможность применять аппарат логарифмических частотных характеристик, обладающий свойством наглядности и простоты. Что касается непрерывности модели для цифровой петли ФАПЧ, то такое допущение оправдано, поскольку частота сравнения, на которой работает ЧФД, значительно превышает ширину полосы пропускания петли по уровню –3 дБ [18]. Основные приемы, особенности построения и использования логарифмических частотных характеристик для суждения об эффективности и устойчивости системы ФАПЧ подробно изложены в [19]. Типовая логарифмическая АЧХ системы ФАПЧ может выглядеть так, как показано на рис. 7.4.4.

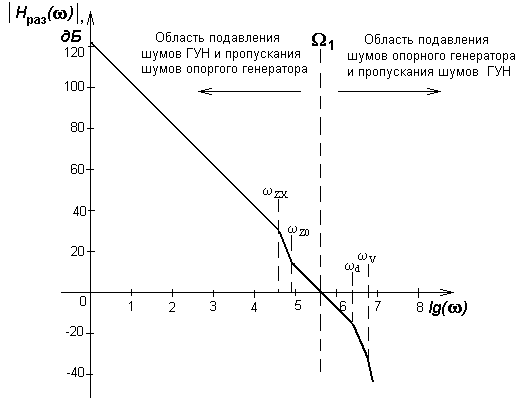
Рис. 7.4.4.

Введем обозначения для мощности основных источников фазовых шумов (помех) в кольце ФАПЧ:

· S_R(w) – спектральная плотность мощности (СПМ) фазового шума на «опорном» входе ЧФД, обусловленного флюктуациями фазы опорного генератора и шумами (помехами) от опорного делителя;

· S_СР(w) – СПМ шума (помех) на выходе ЧФД, связанного с работой самого дискриминатора и его выходного каскада – «зарядового насоса» СР;

· S_V(w) – СПМ фазового шума собственных фазовых флюктуаций колебания ГУН (или фазовой модуляции, когда модулирующее воздействие оказывается непосредственно на сам ГУН).

Считая указанные источники шума некоррелированными, запишем выражение для СПМ фазового шума на выходе синтезатора с ФАПЧ:

Q_S(w) = Q_V(w) + Q_CP(w) + Q_R(w),

где Q_V(w) – часть мощности выходного фазового шума, обусловленная влиянием S_V(w); Q_СР(w) – часть мощности выходного фазового шума, обусловленная влиянием S_СР(w); Q_R(w) – часть мощности выходного фазового шума, обусловленная влиянием S_R(w).

Найдем выражения, описывающие Q_V(w) , Q_CP(w) и Q_R(w).

По отношению к фазе колебания блоки рассматриваемого синтезатора частоты можно представить в операторной форме следующим образом:

· K_d(p) = K_d /(1+pT_d) – блок ЧФД считаем инерционным звеном первого порядка; его сопрягающяя частота w_d = 1/T_d обозначена на рис. 7.4.4.;

· K_V(p) = K_V/(p(1+pT_V)) – блок ГУН считаем комбинацией интегратора и инерционного звена первого порядка, его сопрягающяя частота w_V=1/T_V обозначена на рис. 7.4.4; далее для простоты принимаем K_V(p) = K_V(p)/p;

· Z(p) – петлевой фильтр, вид передаточной функции которого зависит от типа фильтра (см. параграф 7.7, [17-20]), на рис. 7.4.4. его сопрягающие частоты обозначены как w_Z0 и w_ZX;

· 1/N – считаем ДПКД безынерционным делителем полной фазы колебания.

Если записать операторную передаточную функцию разомкнутой петли ФАПЧ от входа ЧФД до выхода ГУН в виде

H_раз(p) = K_d(p)Z(p)K_V(p)/p,

то для операторной передаточной функции замкнутой петли ФАПЧ будет справедливо выражение

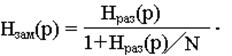
Тогда для вклада в общий уровень выходного шума системы от шумов и помех, поступающих на входы ЧФД, можно записать выражение:

Q_R(w) = |H_зам(jw)|²S_R(w).

Из рис. 7.4.4. видно, что для низких частот |H_раз(jw)| >> 1, следовательно, |H_зам(jw)|»N, и Q_R(w) = N²S_R(w). Отсюда ясно, что низкочастотные шумы и помехи, поступающие на вход ЧФД («внешние»), система ФАПЧ беспрепятственно (и даже с усилением!) передает на выход ГУН. Можно также отметить, что для ослабления проникновения «внешних» помех в спектр выходного колебания синтезатора желательно работать с небольшими значениями N.

Для высоких частот, т.е. лежащих за пределами полосы пропускания петли ФАПЧ (на рис. 7.4.4 – выше частоты среза W₁), |H_раз(jw)|»0 и |H_зам(jw)|»0, что приводит к подавлению высокочастотных флюктуаций фазы «внешних» помех, т.е. Q_R(w) » 0.

Итак, по отношению к «внешним» шумам и помехам, например, шумам фазы (или к преднамеренной угловой модуляции) опорного колебания, петля ФАПЧ ведет себя как ФНЧ, транслируя их на выход синтезатора в полосе частот примерно до частоты среза АЧХ разомкнутой петли W₁.

Если мощность S_СР(w) шума, генерируемого ЧФД, пересчитать на его вход, разделив на коэффициент передачи ЧФД, т.е.

Q_CP(w) = S_СР(w) |H_зам(jw)/K_d(jw)|²,

то выводы о влиянии шумов и помех, порождаемых ЧФД, на спектр выходного колебания синтезатора будут аналогичны сделанным выше для Q_R(w).

Противоположным образом, как ФВЧ, действует петля ФАПЧ на собственные шумы ГУН («внутренние» шумы): она подавляет низкочастотные флуктуации фазы ГУН и пропускает высокочастотную их составляющую (границей раздела областей НЧ и ВЧ здесь опять служит частота W₁). Чтобы убедиться в этом, выпишем выражение для Q_V(w) – части мощности выходного фазового шума, обусловленной наличием S_V(w):

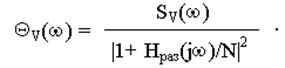
Поскольку H_раз(p) является функцией, обладающей свойствами ФНЧ, см. рис. 7.4.4, то в области низких частот |H_раз(jw)/N| >> 1 и, соответственно, Q_V(w) » 0. Напротив, при w>>W₁ будет выполняться неравенство |H_раз(jw)/N| » 0, откуда следует, что подавления высокочастотных флюктуаций фазы ГУН не будет: Q_V(w) = S_V(w).

Иллюстрацией к вопросу о фильтрации фазовых шумов петлей ФАПЧ может послужить рис. 7.4.5, где на спектре выходного колебания синтезатора на основе ИМС ADF4113, имеющего центральную частоту 900 МГц, можно четко различить две частотные области: низкочастотная - «внешних» шумов, главным источником которых является колебание опорного генератора, и высокочастотная - «внутренних» шумов, связанная с флюктуациями фазы ГУН. Границей раздела (cм. W₁ на рис. 7.4.4) этих областей является частота среза петли, в данном случае равная 20 кГц.

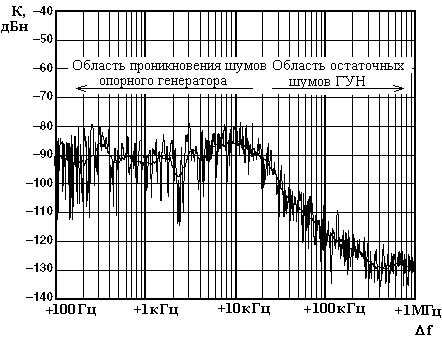
Рис. 7.4.5

Итак, в случае применения простой однопетлевой (однокольцевой) системы ФАПЧ возникает противоречие: для того, чтобы уменьшить влияние фазовых шумов ГУН, необходимо уменьшать инерционность петлевого фильтра, а для снижения проникновения в выходное колебание «внешних» фазовых шумов, нужно действовать противоположным образом, т.е. «утяжелять» фильтр. Иногда эту проблему решают с помощью введения в систему ФАПЧ дополнительных петель авторегулирования. Рассмотрим для примера двухкольцевую систему ФАПЧ (рис. 7.4.6).

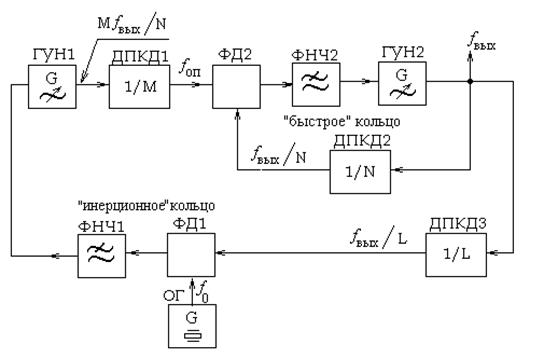
Рис.7.4.6

Внутреннее кольцо этой системы состоит из фазового дискриминатора ФД2, петлевого фильтра ФНЧ2, генератора ГУН2 и делителя частоты с переменным коэффициентом деления N ДПКД2. Фильтр ФНЧ2 делается малоинерционным для того, чтобы успешно подавлять шумы выходного генератора всей системы – ГУН2. Внешнее кольцо ФАПЧ включает в себя элементы ДПКД3 с коэффициентом деления частоты L, ФД1, опорный кварцевый генератор ОГ, ФНЧ1, ГУН1 и ДПКД1 с коэффициентом деления частоты М. Петлевой фильтр внешнего кольца ФНЧ1 является весьма инерционным, за счет чего фазовый шум генератора ГУН1 значительно меньше, чем шум опорного генератора ОГ. Таким образом, для внутреннего кольца ФАПЧ ПГ1 выступает в качестве эталонного малошумящего генератора, следовательно, общий уровень шума в выходном колебании двухкольцевой системы ФАПЧ должен быть меньше, чем у типовой однокольцевой.

Из рис. 7.4.6 видно, что в процессе работы двухкольцевой системы ФАПЧ должны одновременно выполняться два условия:

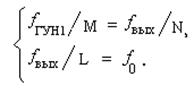
Можно сделать вывод, что для правильного функционирования рассматриваемого синтезатора при смене частоты коэффициент L должен изменяться синхронно с коэффициентами M и N:

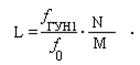
Иногда для оптимизации характеристик системы ФАПЧ ее выполняют многокольцевой – может использоваться три кольца авторегулирования и больше; возможен вариант совмещения в одной системе колец фазовой и частотной автоподстройки частоты.

Вернемся к простому синтезатору с ФАПЧ по схеме рис. 7.4.1. Для повышения рабочей частоты синтезатора перед ДПКД (который может работать на частотах только до сотен МГц) устанавливают предварительный делитель частоты с коэффициентом деления К, при этом и шаг перестройки частоты увеличивается в К раз:

F_вых = (К·F₀ / M)N.

В случае необходимости сохранения на высоких рабочих частотах такого же шага перестройки, как в схеме без предварительного делителя (F₀ / M) применяют схему с перестраиваемым поглощающим счетчиком и двухмодульным предварительным делителем (рис.7.4.7).

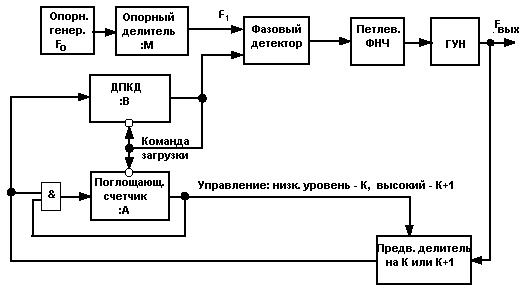
Рис. 7.4.7.

Предварительный делитель в этой схеме имеет переключаемый коэффициент деления: К или К+1 (например, 10/11 или 3/4, такие ИМС выпускаются промышленностью).

ДПКД и поглощающий счетчик работают таким образом, что по команде загрузки они загружаются числом В и А соответственно (причем обязательно В>А), после чего каждый входной импульс уменьшает их состояние на 1. Пока в счетчиках остается число, большее 0, на их выходах присутствует высокий логический уровень, а при достижения 0 этот уровень меняется на низкий.

Схема с поглощающим счетчиком работает следующим образом. Пусть в какой-то момент времени счетчик В обнулился, при этом оба счетчика, согласно схеме, перезагружаются величинами А и В соответственно, и начинается новый цикл счета на уменьшение их значений. Пока поглощающий счетчик не обнулился, на его выходе 1 и предварительный делитель работает с коэффициентом К+1, поэтому он обнулится через (К+1) А периодов частоты ГУН. Как только его значение достигнет 0, на его выходе установится низкий логический уровень, он перестанет считать, а коэффициент предварительного делителя станет равным К. До обнуления счетчика В останется еще (В-А) циклов счета (счетных импульсов). Поскольку счетные импульсы теперь поступают с частотой ГУН, деленной на К, то до обнуления счетчика В пройдет еще (В-А)К периодов частоты ГУН. После обнуления ДПКД описанный цикл повторится.

Итак, подсчитаем эквивалентный коэффициент деления схемы: он равен полному числу периодов частоты ГУН до ее повторной перезагрузки

N = (A(K+1))+((B-A)K) = A+BK.

Частота ГУН при этом описывается той же формулой, что и для простейшей петли ФАПЧ:

F_вых = (F₀ / M)N = (F₀ / M)(A+BK)

Важно здесь то, что теперь изменением коэффициента деления поглощающего счетчика А можно добиться перестройки синтезатора на высокой частоте с малым шагом, равным (F₀ / M). Пределы изменения эквивалентного коэффициента деления N = (К²-К)... (A_max+B_maxK).

Описанный принцип реализован в отечественных ИМС К1015ХК2А (им требуется внешний предварительный делитель с изменяемым модулем счета) и в ИМС семейства ADF4110-ADF4112 (у них этот делитель выполнен на кристалле ИМС).

Рассмотренные выше типы синтезаторов (рис. 7.4.1., рис. 7.4.7) относятся к классу синтезаторов с целочисленным коэффициентом деления частоты N в цепи обратной связи, или «Integer-N» синтезаторам. Существуют синтезаторы с дробно-переменным делителем частоты (ДДПКД), называемые «Fractional-N» синтезаторами, у которых N может иметь изменяемую дробную часть. Их преимуществом является возможность получения заданной рабочей частоты при значительно меньшем коэффициенте деления в цепи обратной связи петли ФАПЧ. При этом обеспечивается и малый шаг сетки частот синтезатора.

Напомним, что из полученной выше формулы Q_R(w) = N²S_R(w), описывающей влияние фазовых шумов опорного генератора на СПМ фазовых шумов выходного колебания синтезатора, следует, что для улучшения спектральной чистоты выходного колебания желательно работать с небольшими значениями N, что невозможно обеспечить для высоких частот синтезатора при малом шаге по частоте. Длительность переходных процессов в синтезаторе также определяется шагом по частоте, который, как было отмечено выше, для любого «Integer-N» синтезатора равен частоте сравнения (F₀ / M).

Проиллюстрируем сказанное примером. Предположим, требуется получить сетку частот в окрестности 50 МГц с шагом 10 Гц. Частота опорного кварцевого генератора составляет F₀ = 1 МГц. В случае применения простой однокольцевой схемы ФАПЧ (рис.7.4.1) коэффициент деления ДПКД составит N = 5000000, коэффициент деления опорного делителя М = 100000. Величина СКО фазового шума опорного генератора, пересчитанная на выход синтезатора, т.е. проникающая в спектр колебания ГУН, будет в N/M = 50 раз больше, чем СКО фазового шума самого опорного генератора. Длительность же переходного процесса установления новой частоты может достигать 10…100 периодов частоты сравнения дискриминатора, что в данном случае составит 1…10 секунд!

Рассмотрим тот же пример при использовании синтезатора частоты с дробно-переменным коэффициентом N («Fractional-N» синтезатора). Существует несколько различных схем таких синтезаторов, но для любой из них можно записать формулу, определяющую значение частоты выходного колебания в следующем виде:

F_вых = F_сравн(N+q/M_F),

где F_сравн – частота сравнения ЧФД, причем, как и для рассмотренных выше схем синтезаторов справедливо соотношение F_сравн = F₀/М; N – целая часть коэффициента деления ДДПКД; q – число, записанное в «дробный» регистр, M_F – значение «модуля-интерполятора»; 0 £ q £ M_F.

Итак, выбираем частоту сравнения F_сравн = 100 кГц; длительность переходного процесса определяется этой частотой и достигает 0,1…1 мс, но шаг перестройки частоты зависит не от частоты сравнения, а от значения модуля-интерполятора. Установив значение «целочисленного» регистра ДДПКД N = 500 и значение модуля-интерполятора M_F = 10000, получим: для q = 0 F_вых = 50 МГц, для q = 1 F_вых = 50,00001 МГц и т.д., следовательно, шаг перестройки по частоте составит требуемую величину 10 Гц.

Рассмотрим упрощенный вариант структурной схемы синтезатора с ДДПКД [20], рис. 7.4.8. Узлы опорного генератора ОГ, опорного делителя частоты ОД, частотно-фазового дискриминатора ЧФД, петлевого ФНЧ и ГУН являются типовыми для любой схемы ФАПЧ и аналогичны рассмотренным выше. Делитель с переменным коэффициентом деления в данной схеме двухмодульный: при подаче на его управляющий вход s логического нуля коэффициент деления равен N, а при s равном логической единице он принимает значение N+1. Управляющий сигнал вырабатывается счетчиком импульсов СИ, имеющим вход для счетных импульсов и импульса сброса содержимого в логический 0. В счетчик СИ пользователем записывается число q, которое служит для сравнения с числом подсчитанных импульсов, поступающих на вход «счет». Выход счетчика СИ равен логической 1 до тех пор, пока содержимое его меньше или равно q, а после того, как счетчиком будет получен q+1 счетный импульс, его выход устанавливается в логический 0. Импульс сброса содержимого счетчика СИ в 0 вырабатывается другим счетчиком – накопителем кода фазы НКФ, который подсчитывает импульсы, следующие с частотой сравнения с выхода опорного делителя частоты. Модуль счета НКФ также определяется пользователем и обозначен здесь как M_F; после формирования сбрасывающего импульса, обнуляющего содержимое СИ, содержимое НКФ также обнуляется.

Рис. 7.4.8.

Начнем рассмотрение работы схемы рис. 7.4.8 с того момента, когда содержимое НКФ и СИ стало равным нулю. Первые q импульсов ГУН с этого момента будут делиться в ДПКД на N+1, а последующие, начиная с q+1 и до прихода с НКФ импульса «сброс», будут делиться по частоте на N. В синхронном режиме периоды импульсных последовательностей на обоих входах ЧФД равны, что можно выразить в виде очевидного равенства, левая часть которого эквивалентна количеству периодов частоты сравнения, поступающих на опорный вход ЧФД, а правая – количеству периодов импульсной последовательности, поступающей на ЧФД с ДПКД за интервал времени между двумя последовательными переполнениями НКФ:

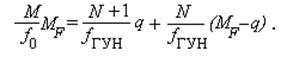
Выражая выходную частоту синтезатора F_вых = f_ГУН из данного равенства, получим:

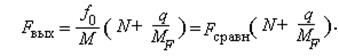
Этой формулой мы уже пользовались выше для описания свойств «Fractional-N» - синтезатора.

Таким образом, синтезаторам частоты с дробно-переменным коэффициентом деления присуще полезное свойство – возможность обеспечение малого шага сетки частот при высоких значениях самой рабочей частоты. Тем не менее, из самого принципа его работы очевиден и его недостаток: постоянное переключение коэффициента деления частоты в ДПКД приводит к паразитной частотной модуляции и, следовательно, появлению нежелательных частотных составляющих в спектре выходного колебания. На рис. 7.4.9 можно увидеть график упрощенной зависимости частоты выходного колебания синтезатора с ДДПКД вида N/(N+1) от времени. Для устранения указанного нежелательного эффекта в выпускаемых промышленностью «Fractional-N»-синтезаторах применяют следующие меры:

- усложняют ДДПКД, предусматривая в нем переключение нескольких коэффициентов деления частоты, например, N, N+1, N-1;

- используют сигма-дельта корректор, который псевдослучайным образом нарушает регулярность переключений коэффициента деления, что помогает «размывать» наиболее интенсивные спектральные составляющие, но увеличивает мощность фазового шума;

- выбирают определенный алгоритм переключения коэффициента деления частоты;

- включают управляемую линию задержки на выходе ГУН [20].

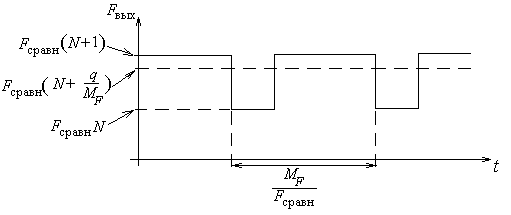
Рис.7.4.9.

В качестве примера интегрального исполнения «Fractional-N» -синтезатора рекомендуем изучить материалы по ИМС семейства AD4250..AD4252 фирмы Analog Devices.

В цифровых приемопередатчиках широко используют сдвоенные синтезаторы частоты - микросхемы, способные формировать одновременно две частоты от одного опорного сигнала. Сдвоенные синтезаторы частоты можно разделить на два типа: ВЧ/ВЧ синтезаторы, вырабатывающие одновременно две высокие частоты, номиналы которых различаются незначительно, и ВЧ/ПЧ синтезаторы, у которых номиналы частот различаются более чем на порядок. В последнем случае ВЧ колебание может вырабатываться с использованием схемы «Fractional-N», а колебание промежуточной частоты - схемой «Integer-N» сдвоенного синтезатора. При этом обе системы ФАПЧ, размещенные на кристалле сдвоенного синтезатора, тактируются от одного опорного генератора, за счет чего их колебания получаются когерентными; благодаря этому обеспечивается возможность когерентной обработки сигналов цифровой радиосвязи [21].

Строго говоря, рассмотренные выше системы ФАПЧ нельзя назвать в полном смысле цифровыми: точнее было бы говорить об импульсных системах ФАПЧ с цифровыми узлами. В настоящее время разрабатываются полностью цифровые системы ФАПЧ, в которых цифровыми методами реализуются все узлы системы, в том числе ЧФД, петлевой фильтр, управляемый генератор; частота последнего в данном случае зависит не от управляющего напряжения, а от кода.

Для дальнейшего изучения интегральных систем ФАПЧ рекомендуем ознакомиться с главой 12 книги [22] – «Проблемы разработки систем ФАПЧ с использованием глубокой субмикронной технологии».

Может быть также полезным для читателей, заинтересовавшихся работой синтезаторов с ФАПЧ, обращение к Интернет-ресурсу www.analog.com/pll/, где представлена интерактивная программа ADIsimPLL, помогающая оценить работу синтезаторов на основе ИМС семейств ADFхххх (ADF4000…4117, ADF4252 и т.д.). Существуют аналогичные «виртуальные» возможности и у других производителей интегральных систем ФАПЧ.