Определение температур нагрева металла.

Как мы отмечали ранее, при нестационарном тепловом состоянии с течением времени происходит изменение температуры тела, т. е. 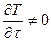. Такое изменение температуры тела возможно, когда тело остывает или нагревается. На практике это широко распространенный процесс нагрева металла. Решение дифференциального уравнения теплопроводности совместно с граничными условиями представляет собой весьма сложную математическую задачу. Мы остановимся на решении при граничных условиях 3-го рода, получившем наибольшее практическое распространение. На практике часто встречаются печи, в которых нагрев металла происходит при неизменной температуре рабочего пространства. Некоторые печи с изменяющейся температурой по длине рабочего пространства можно условно разделить на расчетные участки с приближенно неизменной температурой в пределах каждого участка и к каждому из них применить решения, полученные при граничных условиях 3-го рода.

Решение дифференциального уравнения для удобства заменяют критериальным уравнением следующего вида: 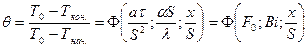, (1)

Где 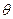- безразмерный температурный критерий;

Т₀ – температура среды печи;

Т_нач. и Т_кон. – температура нагреваемого тела соответственно начальная и конечная.

Из уравнения (1) видно, что температура нагрева металла Т зависит от трех безразмерных комплексов: критериев Фурье (F₀), Био (В_i) и безразмерного геометрического комплекса 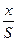, определяющего собой местоположение точки в теле, для которой определяют температуру. Так, для центра нагреваемого тела x=0 и 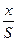=0, для поверхности тела х=S и 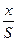=1.

В зависимости от условий решения уравнения Т_кон может представлять собой как конечную температуру поверхности тела (при 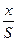=1), так и конечную температуру в центре тела (при 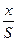=0).

Таким образом, решая уравнение (1) для поверхности тела ( 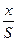=1), получаем температурный критерий: 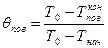, а для центра ( 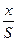=0): .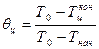

F₀= 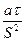- критерий Фурье. Его физический смысл вытекает из того, что главным его членом является время 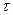. Поэтому критерий F₀ определяет собой время процесса и называется безразмерным временем.

Характер нагрева тел существенно зависит от критерия Вi. Решение уравнения (1) для пластины и цилиндра представлено в виде номограмм Д. В. Будрина в графическом виде.