Динамика вращения твердого тела вокруг неподвижной оси.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТВЁРДОГО ТЕЛА
Вначале найдём выражение для кинетической энергии материальной точки, вращающейся с угловой скоростью 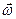 вокруг неподвижной оси OZ.
вокруг неподвижной оси OZ. 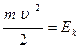 , где m – масса материальной точки. Но
, где m – масса материальной точки. Но  , следовательно:
, следовательно: 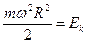
 Величину
Величину 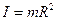 называют моментом инерции материальной точки относительно данной оси. Если выбрана ось OZ:
называют моментом инерции материальной точки относительно данной оси. Если выбрана ось OZ: 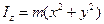 . Таким образом:
. Таким образом: 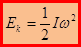 или
или 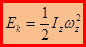 .
.  Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси. Кинетическая энергия i-го малого объема ∆Vi твёрдого тела:
Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси. Кинетическая энергия i-го малого объема ∆Vi твёрдого тела: 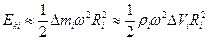
Кинетическая энергия твердого тела:
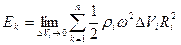 ;
; 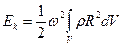 . Или:
. Или: 
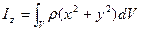 – момент инерции твёрдого тела относительно оси OZ.
– момент инерции твёрдого тела относительно оси OZ.
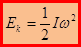 или
или 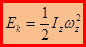
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЁРДОГО ТЕЛА ПРИ СЛОЖНОМ ДВИЖЕНИИ
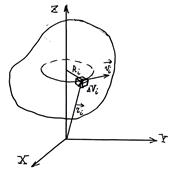
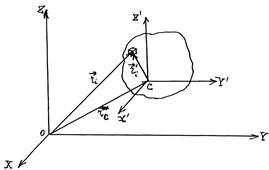 Будем рассматривать сложное движение твердого тела как совокупность двух движений: поступательного со скоростью центра масс тела и вращения вокруг центра масс. Рассмотрим i-ый малый объем ∆Vi твёрдого тела:
Будем рассматривать сложное движение твердого тела как совокупность двух движений: поступательного со скоростью центра масс тела и вращения вокруг центра масс. Рассмотрим i-ый малый объем ∆Vi твёрдого тела:
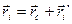 ;
; 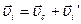 ;
;
Найдём кинетическую энергию этого элемента в системе координат XYZ
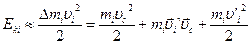
Для нахождения кинетической энергии твёрдого тела необходимо сложить кинетические энергии бесконечно малых объёмов:
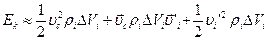 ,
, 
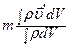 – скорость центра масс тела в системе, связанной с центром масс равна 0.
– скорость центра масс тела в системе, связанной с центром масс равна 0.
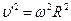 ,
, 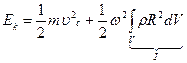
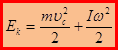 или
или 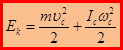
Кинетическая энергия твёрдого тела при произвольном движении равна сумме кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращения вокруг мгновенной оси, проходящей вокруг центра масс.
МОМЕНТЫ ИНЕРЦИИ ТВЁРДЫХ ТЕЛ
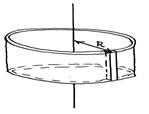 Момент инерции твёрдого
Момент инерции твёрдого 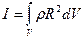 тела есть характеристика самого тела вне зависимости от его вращения. Величины
тела есть характеристика самого тела вне зависимости от его вращения. Величины  и R есть функции координат; интегрирование осуществляется по всему объёму. В общем случае неоднородного (
и R есть функции координат; интегрирование осуществляется по всему объёму. В общем случае неоднородного (  ≠ const) тела произвольной формы вычисление момента инерции является очень сложной задачей. В качестве примеров рассмотрим нахождение моментов инерции некоторых однородных (
≠ const) тела произвольной формы вычисление момента инерции является очень сложной задачей. В качестве примеров рассмотрим нахождение моментов инерции некоторых однородных (  = const) тел правильной формы.
= const) тел правильной формы.
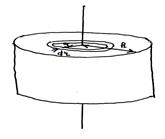
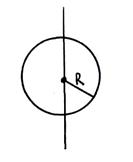
1) Момент инерции тонкостенного однородного цилиндра массы m и радиусом R относительно его оси симметрии:
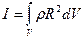 ,
, 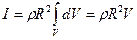 . С учетом
. С учетом 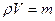 ,
,
получаем 
2) Момент инерции сплошного однородного цилиндра массы m радиусом R и высотой H относительно его оси симметрии:  . Разобьем цилиндр на бесконечно тонкие слои:
. Разобьем цилиндр на бесконечно тонкие слои:
 .
.
С учётом 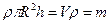 , получаем:
, получаем: 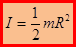
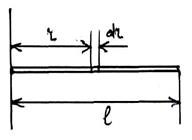 3) Момент инерции тонкого однородного стержня массы m длиной ℓ относительно оси проходящей через его конец перпендикулярно его оси:
3) Момент инерции тонкого однородного стержня массы m длиной ℓ относительно оси проходящей через его конец перпендикулярно его оси:  .
.  .
.
 С учётом
С учётом 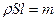 , получаем
, получаем 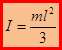
4) Момент инерции однородного шара массы m радиусом R относительно оси, проходящей через его середину. Приведём конечный результат без вывода: 
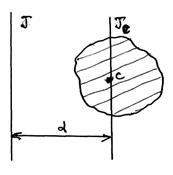 Теорема Штейнера
Теорема Штейнера
В случае, когда момент инерции необходимо найти относительно произвольной оси задача существенно упрощается, если для её решения воспользоваться теоремой Штейнера.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния между осями.
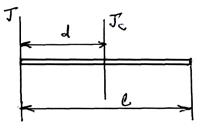
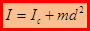
Пример: в соответствии с теоремой Штейнера найдем момент инерции 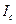 тонкого однородного стержня относительно оси, проходящей через центр масс, если известен момент инерции
тонкого однородного стержня относительно оси, проходящей через центр масс, если известен момент инерции 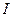 относительно оси, проходящей через конец стержня. Учтём, что
относительно оси, проходящей через конец стержня. Учтём, что 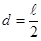 :
: 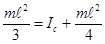 . Получим:
. Получим: 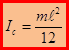 .
.
Дата добавления: 2021-01-11; просмотров: 157;










