Исследование магнитных свойств ферромагнитных материалов

Характерной особенностью ферромагнитных материалов или ферромагнетиков является значительно большая, чем у неферромагнитных материалов, величина магнитной индукции В при одном и том же значении величины напря­женности магнитного поля Н. Внесение ферромагнетика в магнитное поле приводит к упорядочению расположения его атомов, в результате чего появляется дополнительный поток магнитной индукции, обусловленный элементарными токами, существующими внутри атомов.

Величина магнитной индукции В характеризует результирующее магнитное поле в ферромагнитном материале, создаваемое внешними и внутренними возбудителями. Магнитная индукция В зависит от величины напряженности магнитного поля Н, определяемой намагничивающим током I и конфигурацией обтекаемого им проводника, и задается обычно в виде кривой В = f (H).Эта зависимость не имеет точного аналитического выражения и обычно находится экспериментальным путем. В общем случае магнитная индукция В не является однозначной функцией напряженности магнитного поля Н, а зависит и от магнитного состояния, в котором пребывал ферромагнетик до воздействия на него внешнего магнитного поля.

Для исключения влияния начального магнитного состояния ферромагнетика на результаты исследования следует материал подвергнуть воздействию переменного по направлению внешнего магнитно­го поля, постепенно уменьшая величину намагничивающего тока до нуля с таким расчетом, чтобы в конце процесса Н = 0 и В = 0.

В основу расчета магнитных цепей приборов, машин и аппаратов кладется кривая первоначального намагничивания В = f (Н) (рис.1). Для построения кривой В = f (Н), размагниченный образец из ферромагнитного материала помещают в монотонно и медленно нарастающее магнитное поле, отмечая значения Н и В, отвечающие одному и тому же моменту времени.

Р и с у н о к 1 − Кривая первоначального намагничивания ферромагнитного

материала

Имея кривую первоначального намагничивания, можно установить и построить зависимость величины абсолютной магнитной проницаемости m_а ферромагнетика от напряженности магнитного поля Н, т. е. кривую m_а = f(H).Необходимо учитывать, что

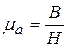. (1)

Величина абсолютной магнитной проницаемости m_а является важнейшей характеристикой ферромагнитных материалов и показывает способность материала намагничиваться в том или ином магнитном поле (рис. 2.).

Р и с у н о к 2 − Зависимость магнитной проницаемости ферромагнетика

от напряженности магнитного поля

Как видно из кривой m_а = f(Н), абсолютная магнитная проницаемость ферромагнетиков изменяется в весьма широких пределах от m₀ (при Н = 0 и Н = ¥) до m_амакс (при Н = Н'). Это затрудняет использование величины m_а для практических расчетов магнитных цепей.

Наибольшее значение абсолютной магнитной проницаемости m_амакс можно определить непосредственно по кривой первоначального намагничивания. Для этого из начала координат 0 проводят касательную 0А к кривой В = f (Н) и находят координаты Н', В' точки касания А (рис.1). Отношение В' к Н' определяет собой наибольшее значение абсолютной магнитной проницаемости m_амакс

m_амакс. (2)

Для ферромагнитных материалов, подвергающихся воздействию переменного по величине и направлению магнитного поля, основной характеристикой является петля гистерезисного цикла, изображающая зависимость величины магнитной индукции В от напряженности магнитного поля Н, т. е. В =f(H).

Следует отметить, что в начале процесса перемагничивания форма петли гистерезисного цикла все время несколько изменяется и только после 10 − 12 циклов перемагничивания устанавливается ее окончательный вид.

Для каждого наибольшего значения напряженности магнитного поля получается своя петля гистерезисного цикла. Совокупность этих кривых, образует семейство симметричных петель с вершинами лежащими на основной кривой намагничивания, причем каждая петля с меньшим значением наибольшей напряженности магнитного поля лежит внутри петли с большим значением Н_макс (рис. 3).

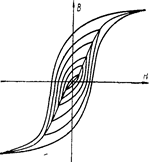
Р и с у н о к 3 − Изменение магнитной индукции в зависимости от величины

напряженности магнитного поля при постепенном уменьшении Н_макс

При увеличении значения Н_макс увеличивается площадь петли гистерезисного цикла, которая характеризует потери энергии за один цикл перемагничивания ферромагнитного материала.

При некотором значении Н_макс получается гистерезисная петля с наибольшей площадью, которая называется предельной (рис. 4) и является важной характеристикой ферромагнетика. Дальнейшее увеличение Н_макс не вызывает измене­ния формы и величины площади петли гистерезисного цикла, а приводит лишь к удлинению участков АF и A'F'.

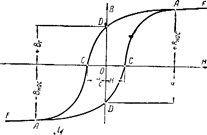
Р и с у н о к 4 − Предельная петля гистерезисного цикла

Наибольшее значение магнитной индукции B_нас, отвечающее значению Н_макс, после которого ферромагнетик не реагирует на дальнейшее возрастание возбуждающего поля, является одной из основных магнитных характеристик материала и называется магнитной индукцией насыщения.

Важные характеристики ферромагнетиков определяются точками пересе­чения D, D' и С, С' предельной петли гистерезисного цикла с осями координат, которые определяют собой соответственно величину остаточной магнитной индукции В_г а также задерживающуюили коэрцитивную силу Н_с.

В зависимости от величины Н_с, характеризующей способность материала сохранять остаточный магнетизм, принято существующие ферромагнетики относить к магнитно-мягким (с Н_с < 8·10² А/м), из которых изготовляются сердечники электромагнитов, и магнитно-твердым (с Н_с > 40·10² А/м), применяемых для изготовления постоянных магнитов.

Зная величину задерживающей силы Н_с, можно ориентировочно определить то значение напряженности магнитного поля Н', при котором абсолютная магнитная проницаемость принимает наибольшее значение 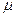_макс из соотношения

Н' = (1,2 − 1,4)·Н_с (3)

На рис.5 приведены петли гистерезисного цикла для различных ферромагнитных материалов.

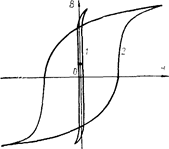
Р и с у н о к 5 − Петли гистерезисных циклов ферромагнетиков

При работе ферромагнетиков в быстро изменяющемся магнитном поле петля гистерезисного цикла получается не­сколько шире, чем при медленном изменении магнитного поля, и носит название динамической петли. Площадь динамической петли характеризует собой полные потери в ферромагнетике за один цикл перемагничивания: потери на гистерезис, вихревые токи, а в некоторых случаях и на последействие вследствие магнитной вязкости материала.

Форма динамической петли зависит от качества испытуемого материала, толщины его листов, максимального значения величины магнитной индукции, а также от частоты изменения намагничивающего тока.

При небольшом значении магнитной индукции динамическая петля эллипсовидная, при средней магнитной индукции − похожа на обычную петлю гистерезисного цикла, а дальнейшее увеличение магнитной индукции вызывает по­степенный переход ее в эллипсовидную форму.

По площади S_п динамической петли, измеренной планиметром, можно определить удельные потери энергии в ферромагнетике на гистерезис и вихревые токи по формуле

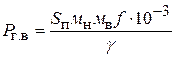, (4)

где Р_г.в − удельные потери в ферромагнетике, Вт/кг;

S_п − площадь динамической петли, см²;

м_н и м_в − соответственно масштабы по осям Н и В, А/м см и Вб/м²·см;

f −частота переменного тока, Гц;

g − вес единицы объема ферромагнетика, г/см³.

Важной магнитной характеристикой ферромагнетиков в быстроменяющемся магнитном поле является его абсолютная амплитудная или динамическая проницаемость m_а~ определяемая как:

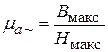, (5)

где В_макс и Н_макс − соответственно максимальные магнитная индукция и напряженность магнитного поля.

Определяются по динамической кривой намагничивания, являющейся геометрическим местом вершин динамических петель. При небольшой частоте f намагничивающего тока и тонких листах ферромагнитного материала динамическая кривая намагничивания практически совпадает с кривой первоначального намагничивания, получаемой при медленно нарастающем значении напряженности магнитного поля, так что m_а~ = m_а.

При исследовании магнитных свойств ферромагнетиков в переменном магнитном поле образцу придается форма замкнутого кольца, собранного из отдельных, изолированных листов испытуемого материала, на котором размещаются две обмотки Iи II с числом витков соответственно w₁ и w₂, выполненных изолированным проводом (рис. 6.).

Р и с у н о к 6 − Образец из ферромагнетика для испытания в переменном магнитном поле

Наличие двух независимых обмоток позволяет измерять ток I в намагничивающей обмотке I и величину индуктированной ЭДС Е в измерительной обмотке II, что дает возможность путем соответствующих расчетов найти отвечающие им наибольшие значения напряженности магнитного поля Н_макс и величины магнитной индукции В_макс.

Действительно, применив закон полного тока

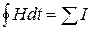(7)

вдоль средней магнитной линии образца из ферромагнетика (рис. 6.), имеем

HpD = Iw₁, (8)

откуда напряженность магнитного поля

, (9)

а ее наибольшее значение Н_макс , А/м будет

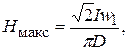(10)

где D − диаметр средней магнитной линии образца, м.

Величина ЭДС Е, наводимая в измерительной обмотке II, будет

Е = 4,44В_максSw₂ , (11)

а наибольшее значение магнитной индукции В_макс, Вб/м²находится из соотношения

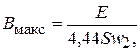(12)

где S − площадь поперечного сечения образца ферромагнитного материала, м²;

w₂ -число витков измерительной обмоткиII.

Подводя к намагничивающей обмотке I различное по величине напряжение, вызывающее появление соответствующего намагничивающего тока I, который возбуждает в ферромагнитном материале магнитное поле можно по соотношениям (10) и (12) и измеренным величинам I и Е найти соответственно значения Н_макс и В_макс, а также по формуле (5) динамическую проницаемость m_а~, что позволяет установить экспериментальные зависимости В = f (Н) и m_а~ = f(H) для исследуемого ферромагнитного материала.

Описанный метод вольтметра и амперметра для снятия кривой магнитной индукции и магнитной проницаемости в магнитном поле тока промышленной частоты является наиболее простым, но и наименее точным (погрешность порядка 10 − 15%) и все же он часто применяется при исследовании образцов из магнитно-мягких материалов.

Магнитные свойства ферромагнетиков можно изучать с помощью электронного осциллографа, который кроме более высокой точности измерения (погрешность порядка 5 – 7 %) позволяет наблюдать влияние различных факторов (деформация, температура и др.) на магнитные характеристики испытуемого материала.

При этом методе на вход Х горизонтальной развертки электронного осциллографа подается потеря напряжения Du, обусловленная мгновенным значением намагничивающего тока i, протекающего по обмотке I и по образцовому сопротивлению r₀ схемы рис. 7, равная

Du=ir₀ , (13)

которая прямо пропорциональна напряженности магнитного поля

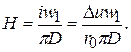(14)

Измерив на экране электронного осциллографа абсциссу е_x,см вершины динамической петли и зная чувствительность S_x, см/В входа горизонтальной развертки X,можно найти наибольшее значение напряженности магнитного поля Н_макс, А/м

(15)

где

(16)

постоянный коэффициент данной экспериментальной установки.

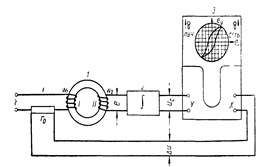
Р и с у н о к 7 − Схема установки для снятия кривой магнитной индукции в зависимости от величины напряженности магнитного поля:

1 − испытуемый ферромагнитный образец;

2 − интегратор;

3 − электронный осциллограф

Мгновенная ЭДС, наведенная в измерительной обмотке II, равна

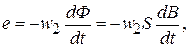(17)

где w₂ −число витков измерительной обмотки II;

S − сечение образца из ферромагнетика, м².

Из соотношения (17) следует, что мгновенное значение магнитной индукции будет

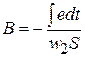, (18)

Следовательно, для того чтобы подать к входу Y вертикальной развертки электронного осциллографа напряжение, прямо пропорциональное величине магнитной индукции в исследуемом образце, необходимо измерительную обмотку II подключить к нему через специальное устройство − интегратор, который обеспечивает автоматическое выполнение соотношения (18).

На рис. 8. приведена схема интегрирующего устройства типа rС, которая входными зажимами II присоединяется к измерительной обмотке, а выходными Y- к выходу вертикальной развертки электронного осциллографа.

Р и с у н о к 8 − Схема интегрирующего устройства

Применяя для цепи интегратора второй закон Кирхгофа, имеем

(19)

где е − мгновенное значение ЭДС с. измерительной обмоткиII;

и_r и и_c − мгновенные значения напряжения на концах соответственно сопротивления r и конденсатора С.

Параметры схемы выбираются такими, чтобы и_r во много раз превышало и_c, что позволяет находить мгновенный ток

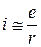, (20)

Тогда мгновенное значение напряжения и_c на конденсаторе С будет

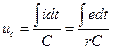(21)

oткуда

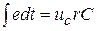(22)

Подставляя найденное значение 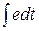в уравнение (18), имеем

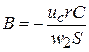(23)

Измерив на экране электронного осциллографа ординату e_y, см вершины динамической петли и, зная чувствительность S_y, см/В входа Y вертикальной развертки, можно найти наибольшее абсолютное значение магнитной индукции В_макс, Вб/м² испытуемого образца как

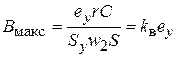, (24)

где

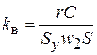(25)

постоянный коэффициент данной экспериментальной установки.

Одновременная подача напряжении Dи и u_c соответственно к входам горизонтальной и вертикальной разверток электронного осциллографа позволяет наблюдать на его экране кривые В = f(H), форма которых для определенного ферромагнетика зависит от величины намагничивающего тока I, протекающего в намагничивающей обмотке I.

Определение динамической кривой намагничивания с помощью электронного осциллографа сводится к измерению абсцисс и ординат вершин симметричных динамических петель и подсчету величин магнитной индукции и напряженности магнитного поля соответственно по формулам (15) и (24).