Основные положения теплового расчета

Рассмотрим изменение температуры первичного (горячего) и вторич- ного (холодного) теплоносителей в теплообменном аппарате рекуперативно- го типа (рис. 5.3). За начало координат принято сечение, через которое втека- ет теплоотдающая жидкость. По оси абсцисс отложена длина трубы или по- верхность теплопередачи F, а по оси ординат – температуры жидкостей; ин- дексами 1 и 2 отмечаются температуры и другие параметры соответственно горячего и холодного теплоносителя. Параметры теплоносителей на входе и

выходе из теплообменного аппарата отмечаются одним и двумя штрихами.

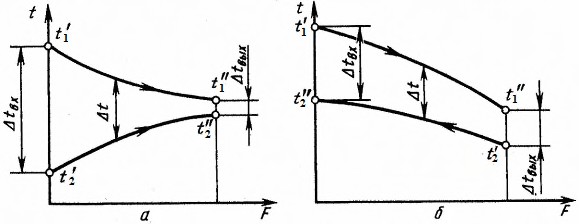
Рис. 5.3. Изменение температуры теплоносителей в рекуперативном ТА:

а – при прямоточном движении теплоносителей без фазовых превращений;

б – при противоточном движении теплоносителей без фазовых превращений

При прямотоке (см. рис. 5.3, а) на входе в теплообменный аппарат раз- ность температур между жидкостями имеет наибольшее значение. При дви- жении жидкостей в теплообменном аппарате разность температур между ни- ми быстро уменьшается, так как жидкости движутся в одном направлении. Температура теплоотдающей жидкости понижается, а температура тепловос- принимающей жидкости увеличивается.

При прямотоке температура тепловоспринимающей жидкости не мо- жет подняться выше температуры теплоотдающей жидкости на выходе из теплообменного аппарата.

При противотоке (см. рис. 5.3, б) температура охлаждаемой жидкости в теплообменном аппарате понижается более интенсивно, так как горячая жид- кость встречает все более и более холодную охлаждающую жидкость, поэто- му при противотоке можно нагреть охлаждающую (тепловоспринимающую) жидкость выше температуры выходящей охлаждаемой (теплоотдающей)

жидкости, т.е. в этом случае возможно t2¢

>> t1¢ .

Разность температур между обеими теплообменивающимися жидко- стями не изменяется очень резко, как это наблюдается при прямотоке. Сред- нее значение температурного напора

Ät= Ätвх - Ätвых

ln Ätвх

Ätвых

(5.1)

при противотоке получается больше, чем при прямотоке (величины Ätвх и Ätвых в случае прямотока и противотока обозначены на рис. 5.3). Поэтому при одной и тоже площади рабочей поверхности F величина теплового потока от горячего теплоносителя к холодному больше при противотоке, чем при пря- мотоке:

F

Q = òÄtdF = k ÄtF , (5.2)

здесь k – коэффициент теплопередачи.

При опытном исследовании теплообменника величина Q может быть определена по изменению энтальпии теплоносителей:

Q = G c

(t¢- t¢) = G c

(t¢- t¢) = Q

1 1 p1 1 1

2 p 2 2 2

2 . (5.3)

Здесь G1и G2– массовые расходы теплоносителей; сp1и сp2– их тепло- емкости. Реально Q1больше Q2из-за потерь тепла через внешний кожух теп- лообменника. Отношение количества теплоты, воспринятой холодным теп- лоносителем, к количеству теплоты, отданной горячим теплоносителем, на- зывается коэффициентом тепловых потерь.

Тепловой расчет теплообменника может быть выполнен с использова- нием понятия тепловой эффективности, представляющей собой отношение теплового потока Q рассматриваемого теплообменника к тепловому потоку Qид, который может передать греющий теплоноситель в идеальных условиях, т.е. бесконечно большого коэффициента теплопередачи или передачи тепло- ты в теплообменнике с бесконечно большой площадью поверхности тепло- передачи:

Q W (t¢- t¢)

W (t¢- t¢)

h = = 1 1 1 = 2 2 2 .

Q W (t¢- t¢)

W (t¢- t¢)

(5.4)

ид min 1 2

min 1 2

Здесь,W1 = G1cp1

W2= G2 cp

– полные теплоемкости массовых расходов теплоносителей; G1и G2– мас- совые расходы теплоносителей; Cp1и Cp2– удельные изобарные теплоемко- сти теплоносителей; Wmin– минимальное значение из W1и W2.

Для однократного перекрестного тока, когда оба теплоносителя абсо-

лютно не перемешаны

{[ (

0 ,78 )

] 0 ,22 }

h1= 1 - exp

exp - S

A - 1 RS

, (5.5)

где A = Wmin/Wmax, R = Wmax/Wmin– функции полных теплоемкостей массовых расходов; S = kF/Wmin– число единиц переноса теплоты в теплообменнике, k

– коэффициент теплопередачи; F – площадь теплопередающей поверхности. Для двукратного перекрестного тока с противоточным включением хо-

дов

⎡⎛1 - h ⎞2

⎤ ⎡ ⎛

1 - h ⎞ ⎤

h2 = ⎢⎜⎜

1 ⎟⎟

- 1⎥

⎢ A⎜⎜

1 ⎟⎟

- 1⎥ . (5.6)

⎢⎣⎝1 - Ah1 ⎠

⎦⎥ ⎢⎣

⎝1 - Ah1 ⎠ ⎥⎦

Вычислив тепловую эффективность h2, с помощью выражения (5.7)

можно определить:

тепловой поток, передаваемый в теплообменнике:

Q = h W

(t¢ - t¢); (5.7)

2 min 1 2

выходные температуры теплоносителей:

Wmin ( )

t1¢ = t1¢ - h2

W1

t1¢ - t2¢

; (5.8)

t2¢ = t2¢ + h2

Wmin(t¢ - t¢)

W

1 2

2

. (5.9)

Таким образом, по уравнениям (5.7), (5.8) и (5.9) определены тепловой поток, передаваемый в теплообменнике, и выходные температуры теплоно- сителей.