Способы графического задания прямой линии

1.Двумя точками (А и В).

Положение прямой линии относительно плоскостей проекций

Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения.

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями - n.

2.2. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями - m.

2.3. Прямые параллельные профильной плоскости проекций называются профильными - р.

3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости оттого, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

3.1. Горизонтально проецирующая прямая – m.

3.2. Фронтально проецирующая прямая – n.

3.3. Профильно проецирующая прямая – р (рис. 93).

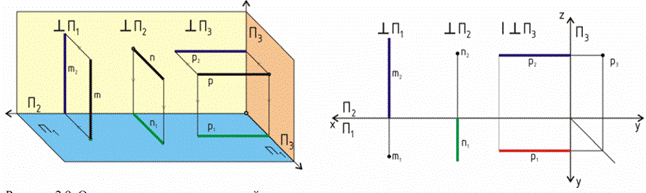
Рис. 93

Вопросы и задания

1. Расскажите о методе ортогонального проецирования. В чем он заключается?

2. Сформулируйте основные свойства ортогональных проекций.

3. Что такое «точка»?

4. Как располагается точка в ортогональной системе двух плоскостей проекций

5. Как располагается точка в ортогональной системе двух плоскостей проекций

6. Дайте определение понятию «прямая линия».

7. Перечислите способы графического задания прямой линии.

8. Расскажите, как может располагаться прямая относительно плоскостей проекций.

Лекция 8

Плоскость. Способы преобразования проекций.

1. Плоскость

Способы преобразования проекций

3. Способ перемены плоскостей проекций.

4. Способ вращения.

5. Вопросы и задания

Плоскость

Плоскость — это поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной на­правляющей прямой.

Плоскостью называют поверхность, которая имеет два измерения и в которой любая прямая, соединяющая две её точки, целиком принадлежит ей.

Плоскость на чертеже может быть задана различными способами:

· тремя точками, не лежащими на одной прямой (рис. 94);

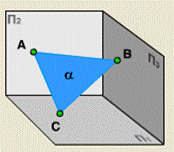
Рис. 94

· прямой и точкой, не лежащей на одной прямой (рис. 95);

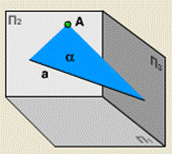
Рис. 95

· двумя пересекающимися прямыми (рис. 96);

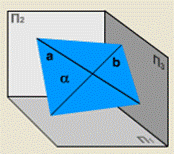
Рис. 96

· двумя параллельными прямыми (рис. 97).

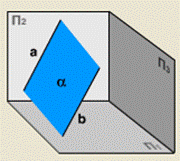
Рис. 97

Плоскости, заданные на чертеже одним из таких способов, не ограничиваются проекциями определяющих ее элементов.

Рассматривая комплексный чертеж плоскости, можно убедиться, что каждый из названных способов задания ее допускает возможность перехода от одного из них к другому.