Лічильники з довільним модулем рахунку

Лічильники з довільним модулем рахунку мають значення М, що відрізняється від цілого ступеню числа 2. Прикладами таких лічильників можуть служити пристрої з M = 10; M = 12; M = 24; M = 60 і т. д. На практиці доводиться мати справу з лічильниками, призначеними для ділення частоти вхідних послідовностей імпульсів у сотні, тисячі і десятки тисяч разів, і далеко не завжди коефіцієнт ділення може бути кратним 2^m (m – ціле число).

При побудові лічильників цього типу використовують такі способи:

· виключення зайвих станів;

· зворотного зв’язку;

· кратних модулів.

Найбільшого розповсюдження набув спосіб виключення зайвих станів. Його реалізація переважно здійснюється наступним чином:

· застосуванням попередньої установки лічильника;

· використанням примусового його обнуління.

На рис. 8.5 приведена схема лічильника, в якому попереднє завантаження початкового стану забезпечується через асинхронні S-входи Т-тригерів за допомогою логіки DD1…DD4 і керуючого входу РЕ (паралельного завантаження). Через входи D₁ , D₂ , D₄ , D₈ у лічильник може бути записаний будь-який двійковий код у діапазоні 0000 – 1111, значення якого буде зафіксоване на виходах Q₁ , Q₂ , Q₄ , Q₈ . Запис коду забезпечується до початку подачі вхідної послідовності імпульсів на С-вхід. Тому з моменту подачі вхідних імпульсів лічильник рахуватиме, починаючи не з нуля, а з занесеного коду.

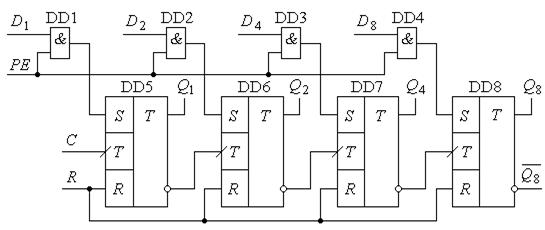
Рис.8.5.

Кількість імпульсів N , що може бути подана на С-вхід лічильника до переповнення, обчислюється за формулою:

N = M – D,

тобто з М станів лічильника виключається D перших станів.

На рис. 8.6 приведені умовні позначення двійкового лічильника (рис. 8.6, а) та лічильника з попередньою установкою (рис. 8.6, б).

На відміну від двійкового лічильника, в позначенні лічильника з попередньою установкою зображені входи D (D₁ ÷ D₈) і допоміжний вхід паралельного завантаження РЕ. Особливість таких лічильників полягає в тому, що при циклічній роботі після завершення кожного циклу необхідно перезаписувати початковий код. Крім того, необхідно враховувати, що двійковий вихідний код у такому лічильнику при D ≠ 0 не відповідає кількості імпульсів, поданих на вхід С.

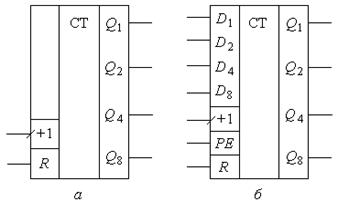
Рис.8.6.

Незважаючи на це, лічильники цього класу знаходять широке використання. Як приклад, можна назвати блок адресації у мікропроцесорах. Вихідний двійковий код лічильника задає адресний простір, за яким процесор звертається до зовнішніх пристроїв та пам’яті. При необхідності переходу на нову програму в лічильник завантажується початкова адреса необхідної програми, і він починає формувати послідовно її адреси.

При використанні в якості віднімаючого, вихідний код лічильника зменшуватиметься від записаного, що широко використовується в різноманітних таймерах. При зменшенні коду до нуля наступним імпульсом лічильник встановиться в код 1111, якщо перед цим знову не буде записаний початковий код.

Примусове обнуління характеризується тим, що із загальної кількості станів М виключаються ті, які своїми значеннями перевищують встановлений модуль перерахунку M_B . Якщо, наприклад, лічильник з M = 16 повинен мати M_B = 12, то всі значення, котрі перевищують 12, повинні бути виключені. Тобто створення лічильника з модулем перерахунку M_B досягається виконанням двох умов:

· обнуління лічильника при досягненні поточним кодом значення M_B ;

· виключення всіх станів, що перевищують M_B .

Перша умова забезпечується, якщо сигнал обнуління: R = M_B .

Для лічильника з M_B = 12 маємо: .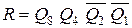

а

б

в

Рис.8.7

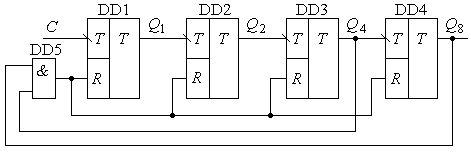
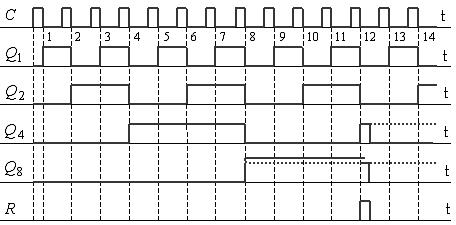
На рис. 8.7, а приводиться приклад схеми двійкового лічильника з M_B = 12, а на рис. 8.7, б – часові діаграми, що пояснюють його роботу. Як витікає з часових діаграм, за зрізом дванадцятого вхідного імпульсу на виходах Q₄ та Q₈ з’являються одиничні сигнали, які створюють сигнал обнуління R усіх тригерів. Враховуючи те, що стан лічильника Q₁ , Q₂ , Q₃ , Q₄ = 0011 є короткочасним (він існує протягом часу обнуління тригерів лічильника). Його можна вважати перехідним і віднести до неробочих.

Таким чином функція виключення зайвих станів, яка забезпечує обнуління лічильника, виглядає наступним чином:

,

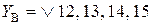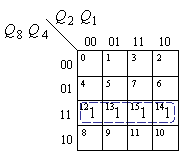
яка після мінімізації за допомогою карти Карно (рис. 8.7, в) прийме вигляд

.

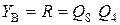Спосіб зворотного зв’язку використовується досить рідко. Особливість цього способу полягає у наступному. Припустимо, що лічильник містить у собі n тригерів. Виділимо з цієї групи меншу – з n₂ тригерами, тоді n = n₁ + n₂ . У виділеній групі заводиться зворотній зв’язок так, щоб при появі одиниць на виходах тригерів перший тригер скидався в нуль. Тоді коефіцієнт перерахунку в цій групі становитиме 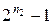, а загальний коефіцієнт перерахунку:

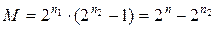. (8.4)

Спосіб кратних модулів пояснюється схемою, що приведена на рис. 8.8.

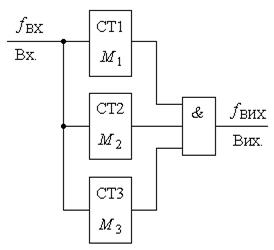
Рис.8.8.

Лічильники СТ1, СТ2, СТ3 з модулями рахунку, відповідно, M₁ , M₂ , M₃ з’єднані по входу паралельно, а їх виходи об’єднані елементом 3І. Імпульс на виході з’явиться лише тоді, коли одночасно на виходах всіх лічильників з’являться вихідні імпульси. У такій схемі частота імпульсів вхідної послідовності f_вх буде ділитися на коефіцієнт M = M₁ M₂ M₃ , і частота вихідних імпульсів матиме значення:

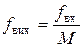. (8.5)