Представление чисел от 0 до 16 в разных системах счисления
| Системы счисления | |||
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0A | |||
| 0B | |||
| 0C | |||
| 0D | |||
| 0E | |||
| 0F | |||
Любая константа N c наперёд заданной точностью может быть представлена в позиционной системе счисления с основанием D в следующем виде (будем рассматривать только целые и положительные D):
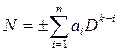 , (1.1)
, (1.1)
где 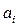 -возможные цифры (0£
-возможные цифры (0£ 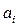 £D-1). Для шестнадцатеричной системы счисления (D = 16) возможными цифрами будут 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f.
£D-1). Для шестнадцатеричной системы счисления (D = 16) возможными цифрами будут 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f.
Число k указывает местоположение запятой. Если k£0, то число N дробное, если 0<k<n, то число N смешанное, если k>n , то число N целое. Величина n определяет требуемую точность представления числа.
В обычной записи чисел знак суммы и степени основания отбрасываются и числа записываются в виде
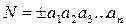 . (1.2)
. (1.2)
Если N – число дробное или смешанное, отделяем запятой целую часть от дробной. Например, число две тысячи четыреста двадцать пять можно записать в десятичной, двоичной, восьмеричной и шестнадцатеричной системе в виде формы (1.1) и (1.2) так:
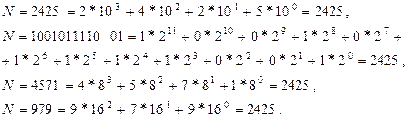
Исторически так сложилось, что в обиходе используется десятичная система счисления, но с появлением вычислительных машин при их программировании стало удобным применять двоичную и шестнадцатеричную систему счислений. Это в первую очередь связано с тем, что элементарная ячейка компьютера бит может находиться только в двух состояниях 0 или 1. Поэтому, двоичное число, например 100101111001 (2425), сразу характеризует, сколько бит (в данном случае 12) необходимо, чтобы хранить число 2425 в памяти компьютера, и в каком состоянии (0 или 1) они должны находиться. Но двоичное число достаточно громоздко, мало того, память ЭВМ организована так, что адресуются не отдельные биты, а совокупность восьми бит называемых байтом. Эта кратность восьми предопределило выбор шестнадцатеричной системы как компактного способа записи констант при программировании.
Поясним сказанное на примере. В одном байте (8 бит) может хранится двоичное число, лежащее в диапазоне от 00000000 до 11111111 (от 0 до 255) или в шестнадцатеричной форме от 00 до FF. Переход от двоичной к шестнадцатеричной системе и обратно можно выполнить очень просто не прибегая к аналитическим выражениям. Для этого необходимо мысленно разбить двоичное число на группы по четыре разряда и поставить каждой группе соответствующее шестнадцатеричное число из табл. 1.1.
Примеры:
1111 1111 = F F;
0101 1100 = 5 C;
00 1001 0111 1001 = 0 9 7 9.
Аналогично переход из шестнадцатеричной системы в двоичную можно осуществить просто, подставляя вместо разрядов шестнадцатеричного числа соответствующие им по табл. 1.1 двоичные представления (1F = 0001 1111).
Переход от десятичной системы к двоичной или шестнадцатеричной более сложен. Для того чтобы его осуществить необходимо разделить десятичное число на соответствующее основание (два или шестнадцать) так, как это показано на примере числа 758.
 или
или 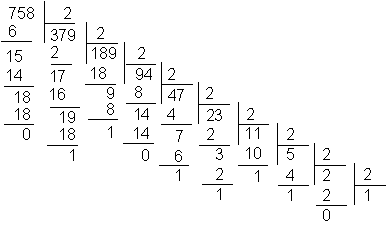
В результате получаем шестнадцатеричное число 2f6 и двоичное число 1011110110. Если применить описанное выше правило перехода от двоичной системы к шестнадцатеричной, то можно увидеть, что результаты совпали.
Чтобы перейти от двоичной или шестнадцатеричной системы к десятичной необходимо воспользоваться выражением (1.1). В случае с числом 758 переход будет выглядеть следующим образом:
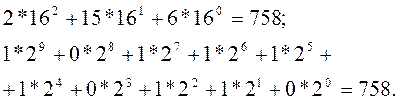
Одну и ту же константу в языке Си++ можно записать в шестнадцатеричном, десятичном и восьмеричном виде. Возможность записать константу в двоичном виде в языке Си++ отсутствует.
2. ЛЕКСИЧЕСКИЕ ОСНОВЫ ЯЗЫКА Си++
Дата добавления: 2020-12-11; просмотров: 658;











