Уравнение Шредингера для электрона в атоме водорода.

Результаты, достигнутые теорией Бора в решении задачи о значениях энергии электрона в водородоподобной системе, были получены в квантовой механике с помощью решения уравнения Шредингера.

Рассмотрим систему, состоящую из неподвижного ядра с зарядом Ze и движущегося вокруг него электрона. Потенциальная энергия электрона

,

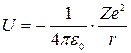где r – расстояние между электроном и ядром. Следовательно, стационарное уравнение Шредингера принимает вид

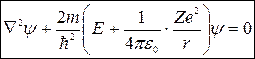
Поле, в котором движется электрон, является центрально-симметричным. Поэтому целесообразно воспользоваться сферической системой координат: r, θ, φ (Рис.1). Это приведет к преобразованию оператора Лапласа

,

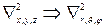Рис.1

Уравнение Шредингера для атома водорода (Z = 1) в сферических координатах примет следующий вид

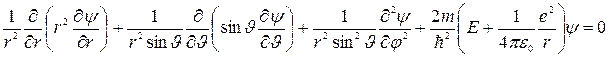
Решение этого уравнения сложно, громоздко и выходит за рамки нашего курса. Отметим только, что решение уравнения Шредингера для атома водорода является точным решением, и это одно из немногих точных решений.