Глава 5. Пространства
В математике пространство определяется как множество однородных объектов (предметов, явлений, состояний, переменных и т. п.), между которыми имеются пространственно подобные отношения. Часто определяют пространство как кортеж 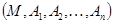 , где
, где  – некоторое множество, а
– некоторое множество, а 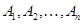 – отношения между его элементами. Иногда о пространстве говорят просто как о множестве
– отношения между его элементами. Иногда о пространстве говорят просто как о множестве  , между элементами которого подразумеваются некоторые отношения.
, между элементами которого подразумеваются некоторые отношения.
Столь широкое понятие пространства сформировалось в результате абстрагирования и обобщения трехмерной эвклидовой геометрии.
Положение точки обычного трехмерного пространства в некоторой системе координат определяется тройкой чисел 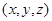 , называемых ее координатами (рис. 6).
Каждой точке соотносится пространственный вектор, выходящий из начала координат и оканчивающийся в этой точке. , называемых ее координатами (рис. 6).
Каждой точке соотносится пространственный вектор, выходящий из начала координат и оканчивающийся в этой точке.
| 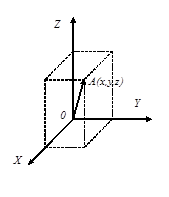
|
| Рис. 6 |
Числа 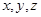 являются проекциями вектора на оси координат и называются компонентами (составляющими) вектора. Как и точка, вектор полностью определяется этой тройкой чисел, если строго соблюдается порядок их следования, т. е.
являются проекциями вектора на оси координат и называются компонентами (составляющими) вектора. Как и точка, вектор полностью определяется этой тройкой чисел, если строго соблюдается порядок их следования, т. е. 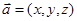 . Итак, между точками и векторами пространства устанавливается взаимнооднозначное соответствие. Поэтому можно говорить о пространстве как о множестве точек или векторов. Так, многие физические величины (силы и скорости, напряженности электрического и магнитного полей и т. д.) представляются векторами, а различные фигуры удобно рассматривать как геометрические места точек, удовлетворяющих соответствующим соотношениям.
. Итак, между точками и векторами пространства устанавливается взаимнооднозначное соответствие. Поэтому можно говорить о пространстве как о множестве точек или векторов. Так, многие физические величины (силы и скорости, напряженности электрического и магнитного полей и т. д.) представляются векторами, а различные фигуры удобно рассматривать как геометрические места точек, удовлетворяющих соответствующим соотношениям.
Действия над векторами сводятся к операциям над тройками чисел. Так, если 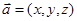 и
и 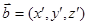 , то
, то 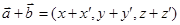 и
и 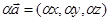 . где
. где 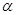 – некоторое число (скаляр). Длина вектора
– некоторое число (скаляр). Длина вектора 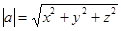 . Расстояние между двумя точками пространства, соответствующими векторам
. Расстояние между двумя точками пространства, соответствующими векторам 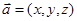 и
и 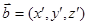 , есть длина вектора
, есть длина вектора 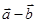 и, следовательно,
и, следовательно, 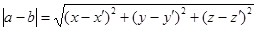 Скалярное произведение двух векторов определяется соотношением
Скалярное произведение двух векторов определяется соотношением 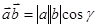 где
где 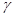 – угол между векторами
– угол между векторами 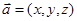 и
и 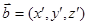 . Отсюда
. Отсюда 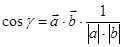 .
.
Единичные векторы (орты), совпадающие по направлению с координатными осями, выражаются соответственно как 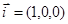 ,
, 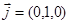 ,
, 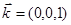 . Каждый вектор однозначно представляется через орты, которые образуют единичный базис в прямоугольной системе координат:
. Каждый вектор однозначно представляется через орты, которые образуют единичный базис в прямоугольной системе координат:
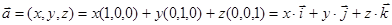 .
.
Формальное обобщение трехмерного пространства состоит в том, что в качестве вектора принимается любая упорядоченная последовательность 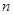 чисел
чисел 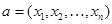 , называемая
, называемая 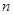 -мерным вектором или точкой многомерного пространства. Числа
-мерным вектором или точкой многомерного пространства. Числа 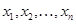 называют компонентами (составляющими, координатами)
называют компонентами (составляющими, координатами) 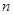 -мерного вектора, а множество таких векторов – числовым или точечным векторным пространством. Определяя соответствующим образом операции над векторами и задавая на множестве векторов отношения, подобные длине, расстоянию, углу и т. п. в обычном пространстве, получают специальные типы пространств.
-мерного вектора, а множество таких векторов – числовым или точечным векторным пространством. Определяя соответствующим образом операции над векторами и задавая на множестве векторов отношения, подобные длине, расстоянию, углу и т. п. в обычном пространстве, получают специальные типы пространств.
До сих пор предполагалось, что количество составляющих вектора конечно и равно 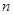 . Ничто не мешает сделать следующий важный шаг на пути расширения понятия пространства: не ограничивать количество составляющих векторов и считать векторами любые (конечные или бесконечные) числовые последовательности
. Ничто не мешает сделать следующий важный шаг на пути расширения понятия пространства: не ограничивать количество составляющих векторов и считать векторами любые (конечные или бесконечные) числовые последовательности 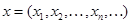 . Такими последовательностями выражаются, например, множество многочленов произвольной степени, ряды, различные разложения функций. Пространство, точки которого определяются бесконечными последовательностями, называется бесконечномерным пространством.
. Такими последовательностями выражаются, например, множество многочленов произвольной степени, ряды, различные разложения функций. Пространство, точки которого определяются бесконечными последовательностями, называется бесконечномерным пространством.
Более того, в качестве элементов пространства можно принять множество непрерывных функций на данном отрезке, совокупность всех решений дифференциального уравнения определенного типа и т. п. В подобных случаях функция 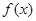 представляется как точка в пространстве, а ее координатами служит бесконечное множество (мощности континуума) значений функции при всевозможных значениях аргумента
представляется как точка в пространстве, а ее координатами служит бесконечное множество (мощности континуума) значений функции при всевозможных значениях аргумента 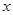 . Пространства, элементами которых являются функции, называются функциональными пространствами.
. Пространства, элементами которых являются функции, называются функциональными пространствами.
Уже отмечалось, что в трехмерном пространстве с понятием вектора связываются различные физические величины, которые характеризуются числовым значением и направлением. Наряду с этим элементы пространства (векторы или точки) могут отождествляться с объектами любой физической природы. Например, в практике широко используется трехмерное цветовое пространство, векторы которого соответствуют цветовым ощущениям и определяются тремя компонентами – интенсивностями красного, зеленого и синего цветов.
Состояние физической системы описывается некоторой совокупностью переменных (токи и напряжения электрической цепи, температуры и концентрации веществ в химическом реакторе и т. п.). Каждое такое состояние можно представить вектором 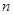 -мерного пространства, называемого пространством переменных состояния. В приведенных примерах объекты пространства характеризуются совокупностью чисел, и эти числа рассматриваются как составляющие соответствующих этим объектам векторов. Можно говорить об отображении множества объектов на множество векторов, но, в конечном счете, отношения между объектами пространства сводятся к отношениям на множестве векторов в числовых пространствах.
-мерного пространства, называемого пространством переменных состояния. В приведенных примерах объекты пространства характеризуются совокупностью чисел, и эти числа рассматриваются как составляющие соответствующих этим объектам векторов. Можно говорить об отображении множества объектов на множество векторов, но, в конечном счете, отношения между объектами пространства сводятся к отношениям на множестве векторов в числовых пространствах.
Но и в случаях, когда объекты характеризуются свойствами, которые не являются числами (форма, цвет, материал), совокупность таких объектов можно также рассматривать как векторное пространство. При этом свойства кодируются с помощью чисел или каких-либо символов, которые можно истолковать как составляющие векторов (объектов) пространства. Подобные коды используют для передачи сообщений, обработки различной информации с помощью вычислительных машин и т. п. В простейших случаях кодирование свойств объектов сводится к простой нумерации, и каждый объект рассматривается как совокупность номеров присущих ему свойств.
Рассмотрим два типа пространств, определяемых как пары ( 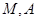 ), где
), где  – множество объектов и
– множество объектов и 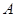 – некоторое отношение на этом множестве.
– некоторое отношение на этом множестве.
Метрическое пространство – это пара ( 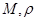 ), где
), где 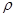 – отношение, называемое метрикой и определяющее расстояние
– отношение, называемое метрикой и определяющее расстояние 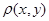 между
между 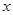 и
и 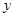 так, что для любых
так, что для любых 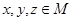 : 1)
: 1) 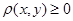 , причем
, причем 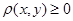 тогда и только тогда, когда
тогда и только тогда, когда 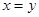 ; 2)
; 2) 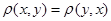 – симметричность; 3)
– симметричность; 3) 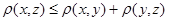 – неравенство треугольника.
– неравенство треугольника.
Расстояние между двумя 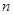 -мерными векторами
-мерными векторами 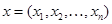 и
и 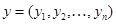 , определенное как
, определенное как 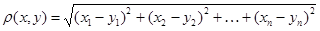 , обобщает понятие расстояния между точками обычного трехмерного пространства.
, обобщает понятие расстояния между точками обычного трехмерного пространства.
Топологическое пространство – это пара ( 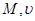 ), где
), где 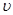 – система подмножеств
– система подмножеств 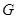 множества
множества  , называемая топологией в
, называемая топологией в  , которая содержит: 1) само множество
, которая содержит: 1) само множество  и пустое множество
и пустое множество 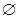 , т. е.
, т. е. 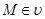 и
и 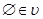 ; 2) пересечение любой пары своих подмножеств, т. е.
; 2) пересечение любой пары своих подмножеств, т. е. 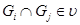 ; 3) объединение любого (конечного или бесконечного) множества своих подмножеств, т. е.
; 3) объединение любого (конечного или бесконечного) множества своих подмножеств, т. е. 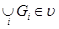 . Из приведенного определения следует, что
. Из приведенного определения следует, что 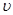 содержит также пересечение любого конечного множества своих подмножеств.
содержит также пересечение любого конечного множества своих подмножеств.
Множества, принадлежащие системе 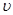 , называются открытыми множествами пространства (
, называются открытыми множествами пространства ( 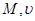 ). Одно и то же множество
). Одно и то же множество  может допускать несколько топологий и при этом получаются различные пространства. Всякое множество
может допускать несколько топологий и при этом получаются различные пространства. Всякое множество  допускает тривиальную топологию, при которой открытыми множествами считаются только
допускает тривиальную топологию, при которой открытыми множествами считаются только  и
и 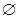 (пространство слипшихся точек), а также дискретную топологию, когда открыто любое подмножество
(пространство слипшихся точек), а также дискретную топологию, когда открыто любое подмножество  .
.
Множества 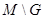 , дополнительные к открытым, называются замкнутыми множествами топологического пространства. Из определения топологического пространства вытекает, что замкнутыми множествами являются: 1)
, дополнительные к открытым, называются замкнутыми множествами топологического пространства. Из определения топологического пространства вытекает, что замкнутыми множествами являются: 1)  и
и 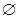 ; 2) объединение конечного числа замкнутых множеств; 3) пересечение любого (конечного или бесконечного) числа замкнутых множеств. Как видно, имеет место дуальность в определении открытых и замкнутых множеств топологического пространства.
; 2) объединение конечного числа замкнутых множеств; 3) пересечение любого (конечного или бесконечного) числа замкнутых множеств. Как видно, имеет место дуальность в определении открытых и замкнутых множеств топологического пространства.
Пусть 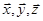 – элементы из множества
– элементы из множества 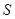 (векторы) и
(векторы) и 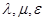 – элементы из поля
– элементы из поля 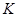 (скаляры). Множество
(скаляры). Множество 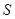 называется линейным пространством над полем
называется линейным пространством над полем 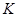 , если на
, если на 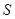 определены два закона композиции:
определены два закона композиции:
1) внутренний (аддитивный) 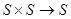 , относительно которого
, относительно которого 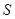 , обладает свойствами: а) коммутативности, т. е.
, обладает свойствами: а) коммутативности, т. е. 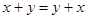 ; б) ассоциативности, т. е.
; б) ассоциативности, т. е. 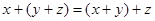 ; в) имеет нейтральный элемент
; в) имеет нейтральный элемент  , такой, что
, такой, что 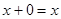 ; г) имеет обратный элемент
; г) имеет обратный элемент 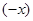 , такой, что
, такой, что 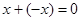 ;
;
2) внешний закон 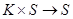 такой, что
такой, что 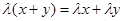 (дистрибутивность относительно внутреннего закона – сложения векторов),
(дистрибутивность относительно внутреннего закона – сложения векторов), 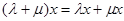 (дистрибутивность относительно аддитивного закона поля
(дистрибутивность относительно аддитивного закона поля 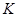 – сложения скаляров),
– сложения скаляров), 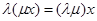 (ассоциативность относительно мультипликативного закона поля
(ассоциативность относительно мультипликативного закона поля 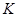 – умножения скаляров),
– умножения скаляров), 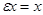 (
( 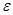 – нейтральный элемент относительно умножения в поле
– нейтральный элемент относительно умножения в поле 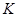 ).
).
Линейное пространство называется действительным (комплексным), если скаляры в его определении берутся из поля действительных (комплексных) чисел. Так, обычные трехмерные векторы образуют действительное линейное пространство. Внутренним законом этого пространства является геометрическое сложение векторов, а внешним законом – умножение вектора на действительное число.
Любое поле 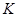 можно интерпретировать как векторное пространство над самим собой (
можно интерпретировать как векторное пространство над самим собой ( 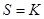 ) со сложением в качестве внутреннего закона и умножением в качестве внешнего закона.
) со сложением в качестве внутреннего закона и умножением в качестве внешнего закона.
Линейное пространство называют также векторным пространством, независимо от природы элементов множества 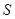 , на котором оно определено.
, на котором оно определено.
В 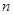 -мерном векторном пространстве внутренней операцией является сумма векторов
-мерном векторном пространстве внутренней операцией является сумма векторов 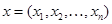 и
и 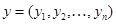 :
:
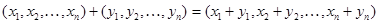 .
.
Нейтральным элементом относительно сложения является нулевой вектор 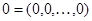 , а обратный к
, а обратный к 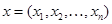 – вектор
– вектор 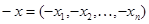 . Внешняя операция – произведение скаляра на вектор определяется как
. Внешняя операция – произведение скаляра на вектор определяется как 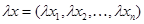 , в результате которой получается вектор той же размерности, что и исходный.
, в результате которой получается вектор той же размерности, что и исходный.
Линейное пространство над числовым (действительным или комплексным) полем называется евклидовым (действительным или комплексным) пространством, если в нем определена операция, называемая скалярным (или внутренним) произведением.
Скалярное произведение, обозначаемое 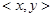 , есть отображение
, есть отображение 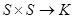 , которое любой паре векторов
, которое любой паре векторов 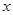 и
и 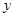 из
из 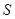 ставит в соответствие число из поля
ставит в соответствие число из поля 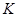 . Оно удовлетворяет следующим аксиомам: 1)
. Оно удовлетворяет следующим аксиомам: 1) 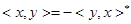 , где
, где 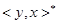 – комплексно сопряженное к
– комплексно сопряженное к 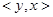 ; 2)
; 2) 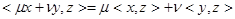 ; 3)
; 3) 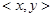 – действительное неотрицательное число, обращающееся в нуль лишь в случае, когда
– действительное неотрицательное число, обращающееся в нуль лишь в случае, когда 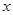 – нулевой элемент.
– нулевой элемент.
Для комплексных 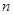 -мерных векторов скалярное произведение определяется как
-мерных векторов скалярное произведение определяется как 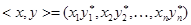 , где
, где 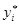 – комплексно сопряженное к
– комплексно сопряженное к 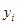 . В случае действительного пространства
. В случае действительного пространства 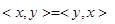 .
.
Через скалярное произведение вводятся: норма (длина) вектора 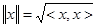 , расстояние между
, расстояние между 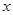 и
и 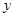 (метрика)
(метрика) 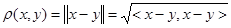 и угол между двумя векторами
и угол между двумя векторами 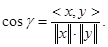
Норму вектора 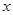 можно рассматривать как частный случай метрики при
можно рассматривать как частный случай метрики при 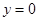 . В общем случае норма, приведенная к внешнему закону линейного пространства, определяется следующими условиями: 1)
. В общем случае норма, приведенная к внешнему закону линейного пространства, определяется следующими условиями: 1) 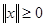 , причем
, причем 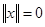 только и если только
только и если только 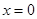 ; 2)
; 2) 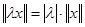 , где
, где 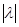 – абсолютное значение из поля
– абсолютное значение из поля 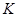 ; 3)
; 3) 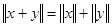 (неравенство треугольника).
(неравенство треугольника).
Пространство, для всех векторов которого определена некоторая норма, называется нормированным пространством.
Вектор, норма (длина) которого равна единице, называется единичным. Два вектора 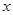 и
и 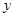 ортогональны
ортогональны 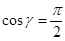 , если
, если 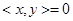 , причем для таких векторов
, причем для таких векторов 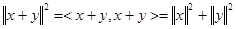 (теорема Пифагора).
(теорема Пифагора).
Конечная совокупность векторов 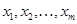 называется линейно-независимой, если соотношение
называется линейно-независимой, если соотношение 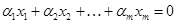 , где
, где 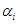 скаляры из поля
скаляры из поля 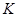 , имеет место только при
, имеет место только при 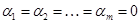 . В случае, когда можно найти такую совокупность скаляров
. В случае, когда можно найти такую совокупность скаляров 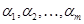 , что хотя бы при одном из них, не равном нулю, справедливо соотношение
, что хотя бы при одном из них, не равном нулю, справедливо соотношение 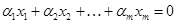 , векторы
, векторы 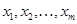 являются линейно-зависимыми (любой
являются линейно-зависимыми (любой 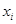 , для которого
, для которого 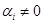 , выражается через другие). Так, четырехмерные векторы
, выражается через другие). Так, четырехмерные векторы 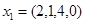 ;
; 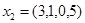 ;
; 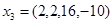 линейно-зависимы, так как при
линейно-зависимы, так как при 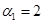 ,
, 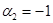 и
и 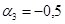 имеем
имеем
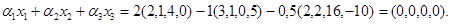
Совокупность независимых векторов 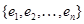 , через которую выражается любой вектор
, через которую выражается любой вектор 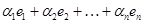 , называется базисом линейного пространства. При этом говорят, что пространство
, называется базисом линейного пространства. При этом говорят, что пространство 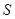 порождено этим базисом, а его размерность (ранг) равна
порождено этим базисом, а его размерность (ранг) равна 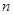 , что записывается как
, что записывается как 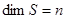 . Базис определяет в
. Базис определяет в 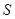 систему координат (систему отсчета). При этом числа (
систему координат (систему отсчета). При этом числа ( 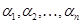 ) являются координатами вектора (точки пространства). Разумеется, координаты одного и того же вектора в различных базисах могут быть различными.
) являются координатами вектора (точки пространства). Разумеется, координаты одного и того же вектора в различных базисах могут быть различными.
Совокупность попарно-ортогональных единичных векторов 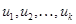 таких, что
таких, что 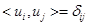 (символ Кронекера
(символ Кронекера 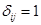 при
при 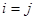 и
и 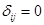 при
при 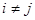 ), образует ортонормированную систему векторов. Число векторов в такой системе не может превышать размерности пространства (
), образует ортонормированную систему векторов. Число векторов в такой системе не может превышать размерности пространства ( 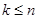 ). Каждая ортонормированная система
). Каждая ортонормированная система 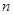 векторов в
векторов в 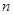 -мерном евклидовом пространстве образует ортонормированный базис.
-мерном евклидовом пространстве образует ортонормированный базис.
Любой вектор 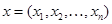 может быть представлен в ортонормированном базисе как
может быть представлен в ортонормированном базисе как 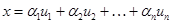 , где
, где 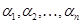 – его координаты в этом базисе. Умножив это равенство скалярно на
– его координаты в этом базисе. Умножив это равенство скалярно на 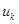 , получим
, получим
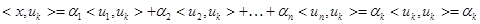 ,
,
так как 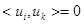 при
при 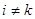 и
и 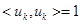 .
.
Следовательно, координаты вектора в ортонормированном базисе выражаются соотношением 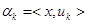 при
при 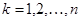 .
.
В 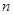 -мерном пространстве существует ортогональный базис, состоящий из единичных векторов
-мерном пространстве существует ортогональный базис, состоящий из единичных векторов 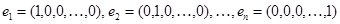 . Компоненты каждого вектора являются одновременно и координатами в системе координат, определяемой этим базисом, так как
. Компоненты каждого вектора являются одновременно и координатами в системе координат, определяемой этим базисом, так как 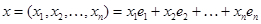 .
.
Дата добавления: 2016-09-06; просмотров: 1955;










