Эквивалентность автоматов-распознавателей

Первый шаг в изложении теории минимизации – понятие эквивалентности состояний.

Два автомата-распознавателя следует считать эквивалентными, если они распознают один и тот же язык.

Теорема.Два автомата-распознавателя будут эквивалентны тогда и только тогда, когда при их синхронном функционировании, под воздействием одних и тех же входных символов, они на каждом шаге всегда одновременно попадают либо оба в заключительные, либо оба в незаключительные состояния.

Справедливость этой теоремы легко доказывается с помощью построения их синхронной композиции и ее анализа. Продемонстрируем это на следующем примере. Пусть два конечных автомата-распознавателя имеют один входной алфавит X, т.е.:

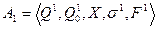и

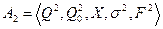
Тогда прямым (декартовым) произведением этих автоматов называется следующий автомат:

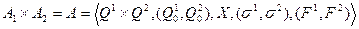
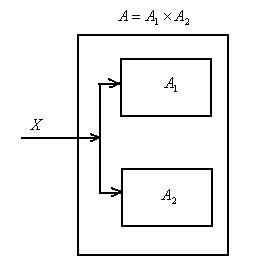
Рис. - Общая структура синхронной композиции двух конечных автоматов

Пересечение двух автоматных языков пусто, если в синхронной композиции конечных автоматов, распознающих заданные языки, из начального состояния не достижимо ни одно состояние, в котором обе компоненты являются заключительными состояниями соответствующих автоматов.

Ни одна цепочка над алфавитом Х, распознаваемая автоматом 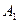, не распознается автоматом 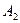и наоборот, что означает, что язык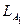и и 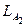в этом примере не пересекаются: .

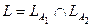Финальное состояние – те состояния, в которых обе компоненты являются одновременно финальными.

Пример. Дано:

Алфавит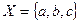

Автоматы 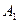и 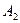работают синхронно под воздействием одних и тех же входных сигналов Х.

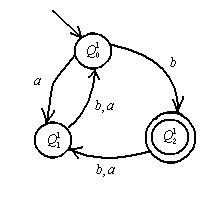
Рис. - Граф переходов автомата-распознавателя

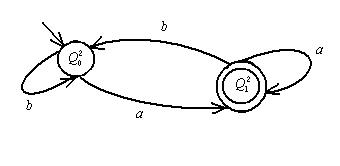
Рис. - Граф переходов автомата-распознавателя

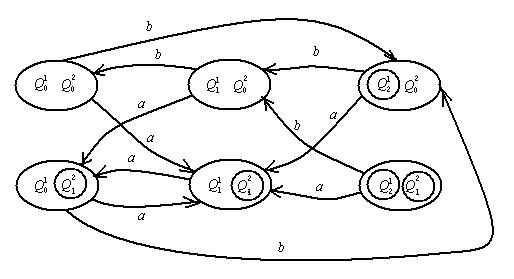
Рис. – Синхронная композиция, граф переходов автомата-распознавателя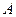

Из графа переходов последнего рисунка видно, что эти два автомата не эквивалентны: например, цепочка ba допускается автоматом 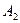и не допускается автоматом 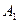(она переводит автомат 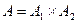из начального состояния 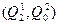в состояние 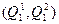, в котором 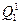- незаключительное состояние автомат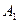а , а 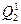- заключительное состояние автомата 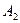. Вообще два конечных автомата-распознавателя будут эквивалентны, если среди достижимых состояний в их синхронной композиции будут только такие пары состояний, в которых обе составляющие либо одновременно заключительные, либо одновременно незаключительные состояния. Тогда любая входная цепочка, допустимая первым автоматом, будет допускаться вторым, и наоборот.

В последнем примере можно видеть, что в синхронной композиции 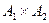из начального состояния не достижимо состояние 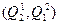- единственное состояние, в котором обе компонентные состояния являются заключительными.

Пример. Дано:

Алфавит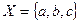

Формальный язык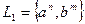

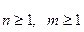
Формальный язык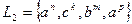

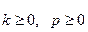
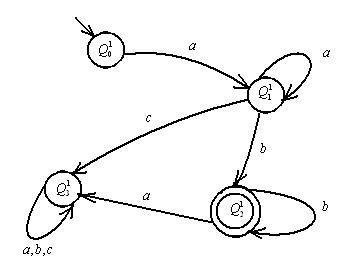
Графы состояний для каждого автомата-распознавателя следующие: