Минимизация автоматов-распознавателей
Перейдем теперь к задаче минимизации конечных автоматов, т.е. к проблеме построения минимального автомата, распознающего тот же язык, что и заданный конечный автомат.
Под минимизацией автомата-распознавателя подразумевается построение минимального автомата кого, что:
1) он обладает минимальным числом состояний;
2) является эквивалентным исходному автомату, т.е. распознает один и тот же язык.
Описание алгоритма минимизации конечного автомата:
1.Находим и удаляем в начальном КА все недостижимые и непродуктивные состояния.
Пример: В следующем КА состояние q3 – недостижимое.

Пример: В следующем КА состояние q3 – непродуктивное.
2.Затем необходимо найти такое разбиение множества всех оставшиехся состояний автомата, чтобы каждое подмножество содержало неразличимые состояния. То есть множества состояний автомата разделяются на классы эквивалентности:
a) В I-й класс относим все конечные/финальные состояния (то есть состояния из множества F);
b) Во II-й класс относим все остальные состояния (то есть Q\F).
Назовем эти состояния 0-эквивалентными.
3. Строим новое одно-эквивалентное разбиение, выделив те состояния, которые по одинаковым символам переходят в 0-эквивалентные состояния.
4. Повторяется шаг 3, последовательно создавая (n+1)-эквивалентные состояния по n-эквивалентным, увеличивая так число классов эквивалентности.
5. Алгоритм заканчивается, когда (n+1)-эквивалентные состояния совпадают с n-эквивалентными.
Каждый полученный класс эквивалентности будет новым состоянием в новом минимизированном автомате.
В множество F' автомата внесём те состояния, которые содержат хотя бы одно финальное состояние из начального.
Полученный, минимизированный КА должен быть эквивалентен начальному КА.
Если на некотором шаге при нахождении k-эквивалентных состояний, состояния 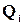 и
и 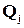 попадают в разные классы эквивалентности
попадают в разные классы эквивалентности 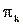 , то на шаге k+1 данные состояния не могут войти в один класс
, то на шаге k+1 данные состояния не могут войти в один класс 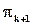 разбиения.
разбиения.
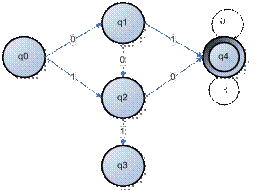
Пример.Пусть задан конечный автомат-распознаватель 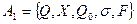 , где
, где 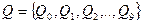 ,
, 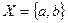 ,
, 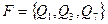 , а функция переходов
, а функция переходов 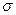 задана графом переходов и расширенной таблицей переходов:
задана графом переходов и расширенной таблицей переходов:
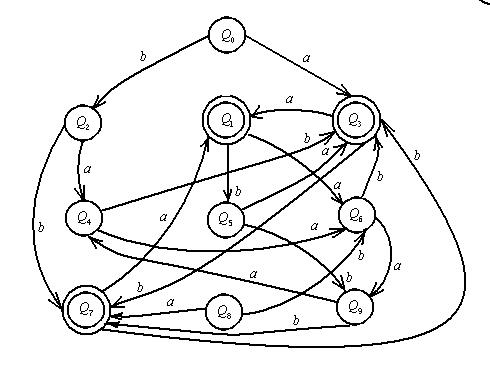
Рис. 1 Граф переходов
| 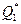
| 
| 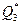
| 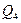
| 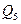
| 
| 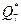
| 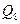
| 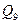
| |
| a | 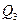
| 
| 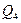
| 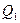
| 
| 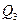
| 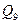
| 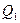
| 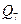
| 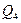
|
| b | 
| 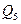
| 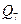
| 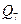
| 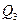
| 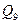
| 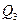
| 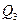
| 
| 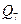
|
Первый шаг. 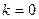
Исходное разбиение  содержит два класса:
содержит два класса:
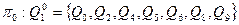
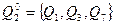
Далее, разбиение 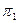 в один блок объединяет те состояния, которые нельзя различить при подаче цепочек длиной 1, т.е. те, которые под воздействием одного и того же входного сигнала переходят в один и тот же блок разбиения
в один блок объединяет те состояния, которые нельзя различить при подаче цепочек длиной 1, т.е. те, которые под воздействием одного и того же входного сигнала переходят в один и тот же блок разбиения  .
.
Поэтому:
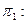
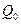
| 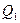
| 
| 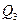
| 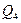
| 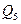
| 
| 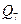
| 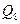
| 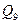
| |
| a | 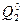
| 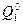
| 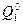
| 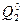
| 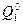
| 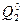
| 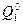
| 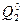
| 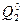
| 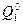
|
| b | 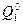
| 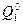
| 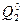
| 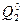
| 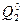
| 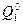
| 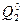
| 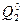
| 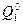
| 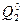
|
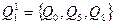
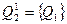
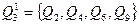
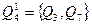
| a | Х | |||||||||
| b | Х |
Следующее разбиение 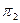 в один блок объединяет те состояния, которые нельзя различить при подаче цепочек длиной 2, т.е. те, которые под воздействием одного и того же входного сигнала переходят в один и тот же блок предыдущего разбиения
в один блок объединяет те состояния, которые нельзя различить при подаче цепочек длиной 2, т.е. те, которые под воздействием одного и того же входного сигнала переходят в один и тот же блок предыдущего разбиения 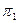 . Итак:
. Итак:

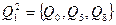
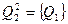
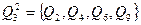
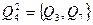
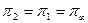
Разбиение 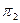 совпадает с разбиением
совпадает с разбиением 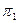 . На основании теоремы искомое разбиение
. На основании теоремы искомое разбиение 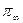 совпадает с
совпадает с 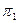 . Таким образом, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих блоки разбиения
. Таким образом, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих блоки разбиения 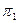 .
.
Введем следующие переобозначения: 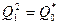 ,
, 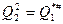 ,
, 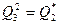 ,
, 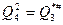 .
.
Тогда таблица переходов этого минимизированного автомата представлена в таблице:
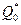
| 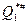
| 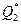
| 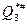
| |
| a | 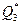
| 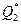
| 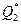
| 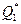
|
| b | 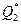
| 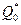
| 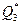
| 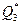
|
Начальным состоянием здесь является состояние 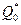 , заключительными - два состояния
, заключительными - два состояния 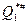 и
и 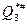 .
.
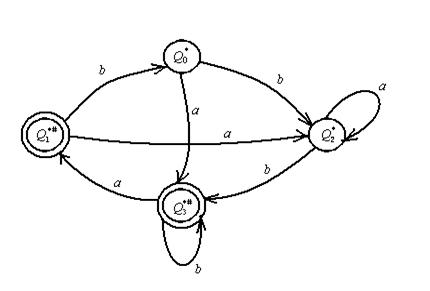
Рис. 1 Граф переходов минимизированного автомата
Дата добавления: 2020-12-11; просмотров: 743;











