Линеаризованное уравнение устойчивости
УСТОЙЧИВОСТЬ ТОНКИХ ИЗОТРОПНЫХ ПЛАСТИН
Лекция 13
Постановка задачи
Расположим оси декартовых координат 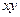 в срединной плоскости изотропной пластины. Будем считать, что пластина нагружена только в срединной плоскости распределенной нагрузкой
в срединной плоскости изотропной пластины. Будем считать, что пластина нагружена только в срединной плоскости распределенной нагрузкой 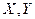 и контурной
и контурной 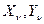 . Поперечная нагрузка отсутствует.
. Поперечная нагрузка отсутствует.
Примем следующие допущения.
I. Нагрузки и опорные реакции действуют строго в срединной плоскости.
2. Изменением размеров в докритическом состоянии можно пренебречь.
3. Все действующие нагрузки “мертвые”.
4. При изгибе пластины справедливы все гипотезы линейной теории изгиба
тонких пластин.
В силу гипотезы I докритическое состояние (индекс “0”) - плоское, т.е. 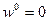 .
.
В силу гипотезы 2 соотношения Коши линейные
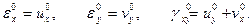 . (13.1)
. (13.1)
Докритическое состояние целиком описывается плоской задачей теории упругости.
Уравнения равновесия
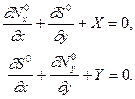 (13.2)
(13.2)
Закон Гука
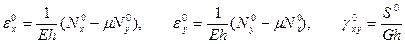 (13.3)
(13.3)
или в обращенной форме
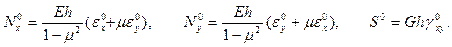 (13.4)
(13.4)
В докритическом состоянии граничные условия на контуре могут быть на разных участках как кинематическими
 , (13.5)
, (13.5)
так и статическими
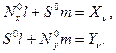 (13.6)
(13.6)
Внешние нагрузки и, следовательно, все докритическое состояние изменяется однопараметрически
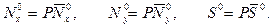 (13.7)
(13.7)
Постановка задачи устойчивости пластин идентична устойчивости стержней: найти наименьшее значение параметра нагрузки 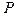 , при котором наряду с устойчивым исходным состоянием плоского равновесия становятся возможны искривленные состояния равновесия.
, при котором наряду с устойчивым исходным состоянием плоского равновесия становятся возможны искривленные состояния равновесия.
Для отыскания таких значений (точек бифуркации) необходимо рассмотреть изогнутое состояние равновесия, бесконечно близкое к исходному
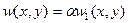 ,
,
где 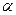 - малый параметр.
- малый параметр.
Для изогнутого состояния в силу гипотезы 4 справедливы соотношения линейной теории изгиба, т.е. выражения для моментов
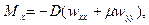
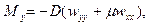
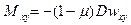 , (13.8)
, (13.8)
где 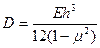 - цилиндрическая жесткость изотропной пластины.
- цилиндрическая жесткость изотропной пластины.
Напомним, что для неизотропных, а для ортотропных пластин, симметричных относительно их плоскости приведения xy, обладающих разными жесткостями по осям x и y, имеем жесткости


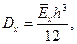
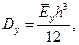
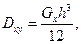
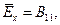
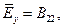
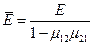
Отметим, что соотношения (13.8) пригодны для записи только линеаризованного уравнения устойчивости. Для исследования закритического поведения пластины этих соотношений недостаточно. Там будут нужны соотношения для “гибких” пластин.
Линеаризованное уравнение устойчивости
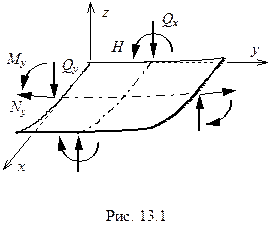 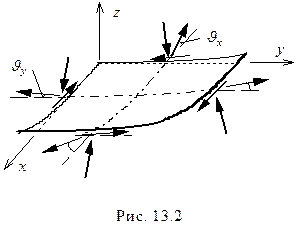
|
Рассмотрим равновесие элемента пластины в изогнутом состоянии, но в осях, связанных с недеформированной срединной плоскостью.
Условия равновесия в плоскости 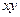 дадут нам уравнения плоской задачи. Это означает, что усилия
дадут нам уравнения плоской задачи. Это означает, что усилия 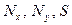 в изогнутом состоянии не отличаются от начальных
в изогнутом состоянии не отличаются от начальных 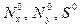 .
.
Запишем сумму моментов всех сил относительно оси 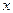 (рис.13.1) . С точностью до б.м. высших порядков это уравнение не будет отличаться от аналогичного в теории изгиба
(рис.13.1) . С точностью до б.м. высших порядков это уравнение не будет отличаться от аналогичного в теории изгиба
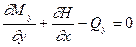 . (13.9)
. (13.9)
Аналогично
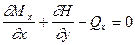 . (13.10)
. (13.10)
В уравнении равновесия проекций всех сил на нормаль в отличие от линейной теории изгиба учтем проекции усилий 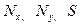 (рис.13.2), наклоненных к осям
(рис.13.2), наклоненных к осям 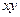 под углами
под углами
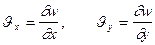 . (13.11)
. (13.11)
Проекция результирующей усилий 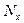 :
:
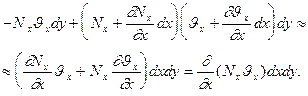
Проекция результирующей усилий 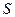 по кромкам с нормалью
по кромкам с нормалью 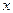 :
:
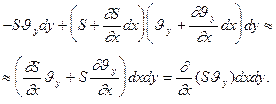
В итоге суммарная проекция всех сил на нормаль:
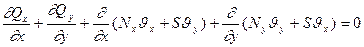 . (13.12)
. (13.12)
Внося в (13.12) выражения для 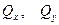 из (9), (10), получаем
из (9), (10), получаем
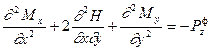
или с учетом (13.8)
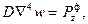 (13.13)
(13.13)
где
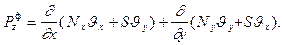 (13.14)
(13.14)
Уравнение (13.13) не отличается от уравнения Софи Жермен, что дает основание называть 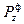
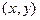 - фиктивной поперечной нагрузкой. Это соображение позволяет получать уравнения устойчивости не только стержней и пластин, но и оболочек из уравнений изгиба путем замены поперечной нагрузки на фиктивную, порожденную проекцией тангенциальных сил.
- фиктивной поперечной нагрузкой. Это соображение позволяет получать уравнения устойчивости не только стержней и пластин, но и оболочек из уравнений изгиба путем замены поперечной нагрузки на фиктивную, порожденную проекцией тангенциальных сил.
Перепишем (13.14) с учетом (13.11) в виде
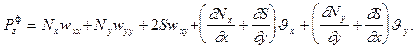 (13.15)
(13.15)
Поскольку 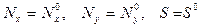 , то из (13.15) с учетом (13.2) следует, что при отсутствии распределенной нагрузки
, то из (13.15) с учетом (13.2) следует, что при отсутствии распределенной нагрузки 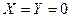
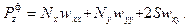 . (13.16)
. (13.16)
Таким образом, для пластины, нагруженной только по контуру, линеаризованное уравнение устойчивости имеет вид
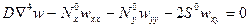 . (13.17)
. (13.17)
В силу первого допущения граничные условия, которым должно удовлетворять решение уравнения (13.17), всегда однородны. Таким образом, при однопараметрической нагрузке (13.7) мы имеем дело с задачей на собственные значения для уравнения
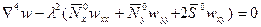 , (13.18)
, (13.18)
где 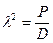 .
.
Требуется найти собственные значения параметра 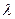 - такие, при которых возможно нетривиальное решение уравнения (13.18), отвечающее однородным граничным условиям. Эти граничные условия формируются так же, как и в теории изгиба пластин. Однако, тут есть некоторые тонкости.
- такие, при которых возможно нетривиальное решение уравнения (13.18), отвечающее однородным граничным условиям. Эти граничные условия формируются так же, как и в теории изгиба пластин. Однако, тут есть некоторые тонкости.
Геометрические (кинематические) граничные условия обычны. Они обнуляют прогиб на контуре 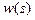 или нормальную производную
или нормальную производную 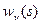 .
.
Статические граничные условия выражают условия равновесия граничных элементов под действием внутренних и контурных сил. Для свободно (шарнирно) опертого или полностью свободного от закрепления и нагрузки края эти граничные условия также имеют обычный вид.
В первом случае
 . (13.19)
. (13.19)
Во втором
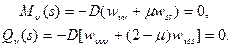 (13.20)
(13.20)
Если же край нагружен “мертвыми”контурными погонными усилиями и при этом свободен от закрепления или закреплен упруго, то контурные нагрузки войдут в граничные условия, однако условия останутся при этом однородными подобно тому, как это было для стержней.
Например, для свободного края 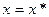 (рис.13.3)
(рис.13.3)
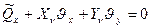 .
.
Обозначив для наглядности 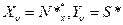 и развернув
и развернув 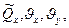 имеем
имеем
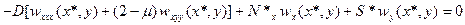 . (13.21)
. (13.21)
Для упруго закрепленного и упруго защемленного края при отсутствии краевой нагрузки условия не отличаются от аналогичных при изгибе:
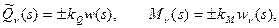 (13.22)
(13.22)
где 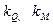 - коэффициенты упругости закрепления.
- коэффициенты упругости закрепления.
Рассмотрим случай, когда край 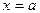 подкреплен упругим стержнем. Мысленно отделим стержень от пластины и приложим усилия взаимодействия.
подкреплен упругим стержнем. Мысленно отделим стержень от пластины и приложим усилия взаимодействия.
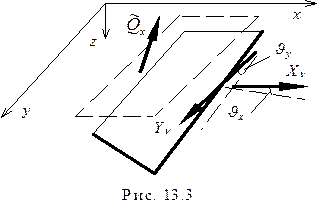 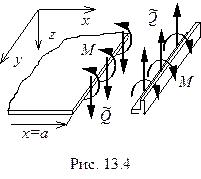
|
Если считать, что стержень работает только на изгиб и не сопротивляется кручению, то для пластины
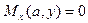 . (13.23)
. (13.23)
Второе условие представляет собой уравнение упругой оси стержня под нагрузкой 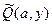
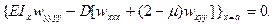 (13.24)
(13.24)
Если сжимающая нагрузка, приложенная к пластине, действует вдоль стержня, и при этом сам стержень загружен продольной нагрузкой 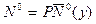 , в условии (13.24) появляется добавочный член от проекции
, в условии (13.24) появляется добавочный член от проекции 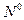 на нормаль к стержню
на нормаль к стержню
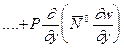 .
.
Знак “+” соответствует 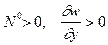 . Если к стержню приложена только сжимающая сила
. Если к стержню приложена только сжимающая сила 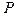 на торце, то
на торце, то 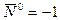 .
.
Наконец, если учесть работу стержня не только на изгиб, но и на кручение под действием контактного момента, который для пластины является изгибающим, а для стержня крутящим, то второе граничное условие для пластины вместо (13.23) примет вид уравнения кручения стержня:
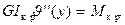
где
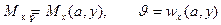 ,
,
или с учетом правила знаков для пластины

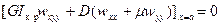 . (13.25)
. (13.25)
(знак “+” соответствует положительному для пластины моменту, который при положительной производной по 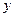 , закручивает стержень в направлении, соответствующем в пластине
, закручивает стержень в направлении, соответствующем в пластине 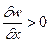 ).
).
Линеаризованное уравнение устойчивости круглых пластин может быть получено либо аналитическим путем, либо непосредственным переходом в (13.13) к полярным координатам. Тогда для основного случая (13.16)
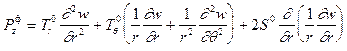 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| в постановке В.З. Власова | | | Тонких прямоугольных изотропных пластин |
Дата добавления: 2016-09-06; просмотров: 1347;










