Параметры Лященко и их использование
Для определения вида частной формулы, параметры которые необходимо прим. В том или ином случае н/знать число Re, которое в свою очередь зависит от скор. 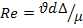
Во избежании этого затруднения Лященко предложил исп-ть безразмерные параметры:
1. A=Re2 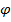
2. B= 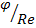 , где
, где 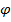 - коэф. сопротив.
- коэф. сопротив.
Найдем 1-ый пар-р Лященко: 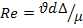 ; Rг/а=
; Rг/а= 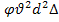 ,
, 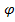 =
= 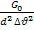 ; Re2
; Re2 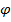 =
= 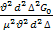 =
= 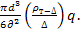
2-ой параметр Лященко: 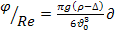
Параметры исп-ся д/отнесения ч-ц к опред-му диапазону по крупности, что позволю прим-ть ту или иную частную формулу д/расчета кон. ск-ти своб. падения.
Ск-ть свободного падения правил. несферичной формы.
Для тел прав-й геом. формы (куб, парал-д, тетраэдр) имеется опред. завис-ть м/у хар-ым размером тела, коэф. сферичности 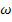 и ск-тью своб. падения. За хар-ый размер таких тел приним. Или диаметр равновеликого по объему шара dэ или d шара поверх-ть кот. равна d тела ds. Коэф-т сферичности:
и ск-тью своб. падения. За хар-ый размер таких тел приним. Или диаметр равновеликого по объему шара dэ или d шара поверх-ть кот. равна d тела ds. Коэф-т сферичности: 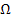 =
= 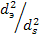 -коэф. сферичности, его легко опред-ть, поскольку объем и пов-ть тела легко вычислить. д/опред
-коэф. сферичности, его легко опред-ть, поскольку объем и пов-ть тела легко вычислить. д/опред 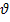 (конечн.)частиц прав. Геом. формы:
(конечн.)частиц прав. Геом. формы: 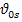 =P
=P 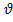 0 (по поверх-ти) P- коэф-т, зав-ый от формы,
0 (по поверх-ти) P- коэф-т, зав-ый от формы, 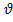 0-ск-ть паден. шара экв-го телу по объему.
0-ск-ть паден. шара экв-го телу по объему.
Если 0,25< 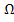 <1;то коэф-т P=
<1;то коэф-т P= 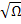 , что хар-но для чисел
, что хар-но для чисел 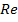 s<20. При числах
s<20. При числах 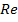 >500, коэф-т: P=1,245
>500, коэф-т: P=1,245 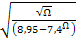 ,
, 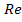 s>500. Зав-ть коэф-та
s>500. Зав-ть коэф-та 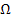 можно опред. по графику, табл.
можно опред. по графику, табл.
Дата добавления: 2020-12-11; просмотров: 581;











