Задачи на прокладку пути судна с учетом постоянного течения
Абсолютной (относительно земной поверхности) скоростью судна при плавании с учетом течения является результат геометрического сложения скорости перемещения судна относительно водной среды и вектора скорости течения.
При плавании с учетом постоянного течения решаются прямая и обратная задачи на прокладку пути судна.
Прямая задача. Найти линию пути ПУb, если известны ИК (КК), Vл, направление течения (Кт) и его скорость (Vт).
Решение:
1. От начальной точки (рис. 4.1) по линии ИК отложим в масштабе карты вектор скорости судна Vл.
2. От конца этого отрезка отложим в том же масштабе вектор скорости течения Vт.
3. Прямая, проведенная между начальной и конечной точками вектора течения, называется линией пути ПУb.
Угол между направлением истинного меридиана и линией пути называется путевым углом на течении ПУb, а угол между линией ИК и линией пути – углом сноса течением b (поправка на течение):
ПУb = ИК + b.
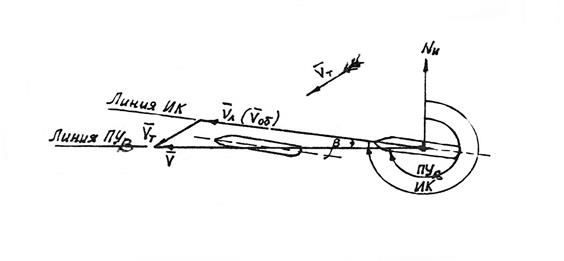
Рис. 4.1
Обратная задача. Найти КК (ИК), когда задан ПУb и известны Vл, Кт, Vт (рис. 4.2).
Решение:
1. От начальной точки проведем линию пути ПУb.
2. От этой же точки отложим вектор скорости течения Vт.
3. От конечной точки вектора скорости течения раствором измерителя, равным скорости судна Vл, сделаем засечку на линии пути ПУb
4. Проведем из начальной точки 0 прямую, параллельную прямой АВ, и получим линию ИК.
5. Рассчитаем КК = ИК – DK.
6. Угол сноса течением (поправка на течение) определим по формуле
b = ПУb – ИК.
Формулы алгебраические, поэтому знак угла b определяется следующим образом: если течение направлено в левый борт, то величина угла записывается со знаком "+", если в правый – со знаком "–".
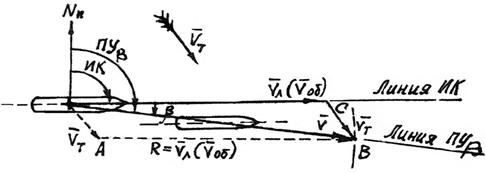
Рис. 4.2
При оценке точности счислимого места судна при плавании на постоянном течении погрешности в элементах течения будут такими же, как погрешности счисления на отдельном курсе. Применяем следующую формулу:
 ,
,
где Мт – погрешность счисления из-за погрешностей в элементах течения.
Величина погрешности счисления Мт из-за погрешностей в элементах течения будет легко определена, если мы условно сделаем замену: Кт = К, Vт = V0. Тогда
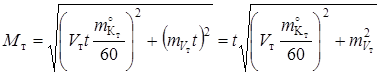 .
.
Таким образом, погрешность счисления прямо пропорциональна времени плавания, она увеличивается также и при увеличении скорости течения.
Если плавание на постоянном течении осуществляется по одному курсу, то погрешность счисления определяется по формуле
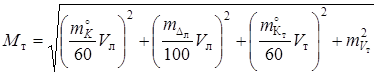 .
.
Можно указать ориентировочные максимальные значения погрешностей для течений в открытом море: скорости – до 0,5 уз, направления – до 30°.
Пример решения задачи.Исходные данные указаны в таблице.
| Номер п/п | Судно по счислению прошло | Расстояние |
| за 2 ч 07 мин по ИК1 = 305,0° | S1 = 27 миль | |
| за 3 ч 48 мин по ИК2 = 253,0º | S2 = 54 мили | |
| за 1 ч 55 мин по ИК3 = 90,0º | S3 = 18 миль |
При переходе учитывалось действие постоянного течения на SE, Vт = 2,2 уз.
Вычислить радиус круга погрешностей конечной счислимой точки, если mк = ±1,5°, mDл = ±1,8 %, mКт = ±18º, mVт = ±0,3 уз.
Решение:
1. Используя табл. 4.1, по аргументам mк и mDл определяем Мn'= 0,308 мили на каждые 10 миль плавания, а затем рассчитываем радиусы погрешности:
М1 = 0,308 · 2,7 = 0,833 мили,
М2 = 0,308 · 5,4 = 1,663 мили,
М3 = 0,308 · 1,8 = 0,555 мили.
2. Рассчитываем Мт:
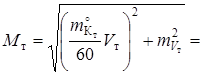 (02h07m + 03h48m + 01h55m) ×
(02h07m + 03h48m + 01h55m) ×
× 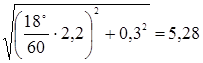 миль.
миль.
3. Определяем Мс
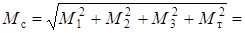
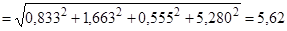 миль.
миль.
Это и будет радиус круга погрешностей счислимой точки. Внутри такого круга с вероятностью 63 ¸ 68 % находится судно. Образец заполнения расчетной таблицы и оформления прокладки графического счисления пути судна с учетом течения приведен в приложении 10.
Дата добавления: 2019-05-21; просмотров: 720;











