Задачи на счисление пути судна с помощью меркаторской карты
С помощью меркаторской карты решаются следующие задачи:
· определение координат любой точки, нанесенной на карте;
· нанесение точки на карту по заданным координатам;
· определение направлений движения судна и прокладка на карте заданных направлений;
· измерение расстояния между двумя заданными точками, нанесение на карту по заданному направлению известного расстояния;
· приведение магнитного склонения к году плавания.
Приведение магнитного склонения к году плавания выполняется в следующем порядке:
а) определяем по карте элементы склонения, расположенные в непосредственной близости от места судна. Если место судна находится между двумя картушками (надписями), то выборка склонения осуществляется путем общей интерполяции;
б) находим на той же карте значение годового изменения магнитного склонения, указанное в ее названии, и год приведения, с их учетом рассчитываем величину склонения на текущий год;
в) добавив рассчитанное изменение склонения к выбранной на карте величине магнитного склонения, получаем значение склонения на год плавания.
Примеры решения задач: 1. Магнитное склонение, выбранное на карте, изданной
в 1983 г., равно 4,0°E. Годовое увеличение – 0,1°. Определить магнитное склонение в 2005 г.
Решение: Определим промежуток времени: 2005 – 1983 = 22 года.
Найдем Dd = 0,1º · 22 = 2,2º.
Магнитное склонение в 2005 г. d = 4,0º + 2,2º = 6,2ºЕ.
2. В районе плавания (в 2005 г.) выберем склонение 15,2ºW. В заголовке карты указано, что склонение приведено к 1995 г. и ежегодное его уменьшение равно 9,0'. Определить склонение в данном районе на год плавания.
Решение: За 10 лет (2005 – 1995 = 10) склонение уменьшится:
Dd = 9,0' · 10 = 90,0' = 1,5º.
Следовательно, в 2005 г.:
d05 = 15,2º – 1,5º = 13,7ºW.
3. Магнитное склонение, выбранное на карте, изданной в 1976 г., равно 1,2ºW. Годовое уменьшение равно 0,17º. Определить магнитное склонение в 2005 г.
Решение: Определим промежуток времени: 2005 – 1976 = 29 лет.
Найдем Dd = 0,17º · 29 = 4,9º.
Магнитное склонение в 2005 г. равно
d05 = –1,2º + 4,9º = 3,7ºE.
Таким образом, вестовое склонение, уменьшаясь, стало равно нулю, а затем, когда магнитный меридиан перешел к востоку от истинного меридиана, начало возрастать остовое склонение и к 2005 г. достигнет значения 3,7º.
Задачи на прокладку пути судна с учетом склонения и девиации,
без учета дрейфа и течения.
Расчет моментов открытия и скрытия огней.
Момент прихода на траверз ориентира
Основные формулы и определения.При графическом счислении с использованием карты решаются следующие задачи:
· перевод и исправление направлений;
· учет магнитного склонения и девиации;
· определение дальности видимости предметов;
· нахождение счислимого места на данный момент. Счисление – это учет движения судна с целью определения его места на любой заданный момент по известному предыдущему месту и элементам движения судна (курсу и скорости). Для нахождения счислимой точки на данный момент, необходимо знать время Т1 и ОЛ1 начальной точки и время Т2 и ОЛ2 в точке прихода.
Рассчитываем разность отсчетов лага РОЛ1:
РОЛ1 = ОЛ2 – ОЛ1.
Зная РОЛ1 и Dл % (или Кл), находим пройденное расстояние Sл, которое откладываем от исходной точки по линии ИК;
· нахождение счислимого места на момент прихода ориентира на траверз или заданный курсовой угол (КУ). Для этого используем формулы:
ИП = ИК ± 90º,
ИП = ИК ± КУ (+пр/б, –л/б).
Затем находим ОИП = ИП ± 180º. Это направление откладываем от ориентира до пересечения с линией ИК;
· нахождение счислимого места на момент открытия (скрытия) маяка. Выбрав по карте значение дальности видимости маяка Дк и зная высоту глаза наблюдателя е, рассчитываем дальность видимости огня Дпр. На графике из точки расположения маяка проводится окружность радиусом, равным величине Дпр, и делается засечка на линии истинного курса, которая и будет являться счислимым местом на момент открытия (скрытия) огня маяка.
Образец заполнения расчетной таблицы и ведения графического счисления указаны в приложении 4, учебные таблицы девиации – в приложении 5, пройденное по лагу расстояние – в приложениях 6, 7, таблицы скоростной девиации – в приложении 8.
Прокладка пути судна с учетом поправки компаса,
лага и дрейфа. Определение радиальной погрешности счислимого места
Основные формулы и определения.Лаг служит для измерения скорости и пройденного расстояния. Чтобы избежать погрешности в измерении данных параметров, каждый лаг имеет поправку Dл, которая выражается в процентах. Поправка лага может быть учтена в виде коэффициента Кл.
Поправку лага Dл рассчитываем по формулам:
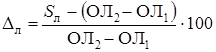 ,
,
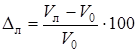 ,
,
где Sл – истинное расстояние, пройденное судном за время t; ОЛ2 – ОЛ1 – разность показаний лага за то же время; Vл – истинная скорость судна относительно воды (Dл учтена); V0 – средняя скорость судна по показателям лага (РОЛ за 1 час).
Учитывать поправку лага можно в виде коэффициента лага:
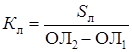 ,
,
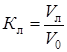 ,
,
 .
.
В МТ-75 содержатся специальные таблицы-вкладыши. Аргументами для входа в таблицы служат:
– разность отсчетов лага ОЛ2 – ОЛ1;
– поправка лага со знаком "+" (при Кл > 1) (приложение 6) или со знаком "–" (при Кл < 1) (приложение 7).
По этим аргументам выбирается расстояние, пройденное судном относительно воды.
Эти же таблицы могут быть использованы для расчетов поправки лага, которая выбирается из таблицы обратным входом по аргументам ОЛ2 – ОЛ1 и Sл.
Точность получения счислимого места при графическом счислении пути судна без учета влияния дрейфа и течения зависит от определения:
1) средней квадратической погрешности mк, характеризующей точность курсоуказания компаса и состоящей из квадратической суммы средней квадратической погрешности отсчета курса mкк и средней квадратической погрешности поправки компаса mDк;
2) средней квадратической погрешности пройденного судном расстояния ms. Для определения расстояния по лагу используется формула
 ,
,
где mDл – средняя квадратическая погрешность поправки лага; Sл – пройденное судном расстояние.
Величина ms полностью зависит от погрешности в поправке лага mDл.
3) погрешностей графических построений на карте, которые при соответствующих масштабах используемых карт практического значения для судовождения не имеют, так как очень малы, поэтому ими можно пренебречь.
Для практических целей точность счислимого места оценивается кругом погрешностей, имеющим радиус Мс, величина которого определяется по формуле
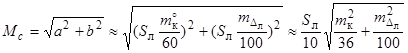 .
.
Для облегчения расчета радиуса круга погрешностей Мс при различных mк и mDл на каждые 10 миль плавания одним курсом (неизменным) можно воспользоваться заранее составленной табл. 4.1.
Таблица 4.1
| mк | mDл,% | |||
| 1º | 0,202 | 0,226 | 0,346 | 0,437 |
| 2º | 0,364 | 0,403 | 0,461 | 0,532 |
| 3º | 0,533 | 0,561 | 0,604 | 0,659 |
| 4º | 0,706 | 0,728 | 0,760 | 0,805 |
Если плавание совершалось по нескольким курсам, то радиус круга погрешностей Мс счислимого места вычисляется по формуле
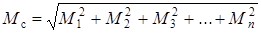 ,
,
где Мn – радиусы кругов погрешностей счислимых мест, вычисленные для каждого отдельного курса.
Линия, по которой фактически перемещается судно под влиянием ветра, называется линией пути при дрейфе (ПУa). Угол между линией истинного курса и линией пути при дрейфе называется углом дрейфа a, или поправкой на дрейф.
ПУ = ИК + a,
ИК = ПУ – a.
Формулы алгебраические, поэтому знак угла дрейфа определяется следующим образом:
а) если ветер дует в левый борт, угол дрейфа считается положительным и записывается со знаком "+";
б) если ветер дует в правый борт, угол дрейфа считается отрицательным и записывается со знаком "–".
При ведении прокладки пути судна с учетом дрейфа на карте указывается только линия пути при дрейфе, на которой откладывается пройденное расстояние Sл.
Для оценки точности счисления при плавании с учетом дрейфа применяются те же формулы и приемы, что и для плавания без учета дрейфа. Различие состоит лишь в том, что вместо погрешности курса mк, в основном равной ошибке в поправке компаса, должна учитываться погрешность путевого угла
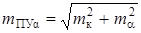 ,
,
где ma – средняя квадратическая погрешность в учитываемом угле дрейфа.
Примеры решения задач: 1. Дано: ОЛ2 – ОЛ1 = 25 миль, DЛ = +5 %. Рассчитать Sл.
Решение. В таблицах приложения 8 с учетом аргументов РОЛ и Dл выбираем величину Sл = 26,2 мили.
2. Дано: ОЛ2 – ОЛ1 = 20 миль; Sл = 19 миль. Рассчитать поправку лага Dл.
Решение: Показания лага больше истинного расстояния, знак поправки должен быть "–" (приложение 9). Учитывая аргументы РОЛ и Sл (обратным входом), находим, что Dл = –5 %.
3. На участке перехода плавание судна осуществлялось по курсам, указанным в таблице.
| ИК1 = 120,0º | Sл1 = 25 миль | mк1 = 1,2º | mDл1 = 1,5 % |
| ИК2 = 210,0º | Sл2 = 18 миль | mк2 = 2,3° | mDл2 = 1,9 % |
Вычислить среднюю квадратическую (радиальную) погрешность конечного счислимого места.
Решение.
1. Рассчитаем радиусы кругов погрешностей Мn счислимых мест плавания по каждому отдельному курсу:
а) по ИК1 = 120,0º: используем табл. 4.1, по аргументам mк1 = 1,2º
и mDл1 = 1,5 % находим путем простой интерполяции значение радиуса круговой погрешности на 10 миль плавания М1; судно прошло 25 миль, рассчитываем М1 = 0,247 · 2,5 = 0,617 мили;
в) по ИК2 = 210,0º: из табл. 4.1 по аргументам mк2 = 2,3º и mDл2 = 1,9 % находим путем простой интерполяции значение радиуса круговой погрешности на 10 миль плавания М2; судно прошло 18 миль, рассчитываем М2 = 0,442 · 1,8 = 0,794 мили.
2. Определяем радиальную погрешность счислимого места при плавании по нескольким курсам:
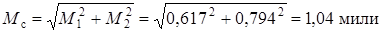 .
.
С помощью циркуля в конечной счислимой точке очерчиваем окружность радиусом 10,4 кб, в пределах которой с вероятностью 63–68 % находится счислимое место судна при условии, что погрешность исходной точки счисления равна нулю.
4. От исходной точки, средняя квадратическая погрешность М0 которой равна 6 кб, ведется графическое счисление с учетом дрейфа; ИК1 = 128,0º, S1 = 25 миль, a = 6,0º, mк1 = ±1,5º, mDл1 = ±2,0%, ma1 = +1,0% ; ИК2 = 285,0º, S2 = 15 миль, d2 = 4,0º, mк2 = ± 2,0º, mDл2 = ±1,5%, ma2 = ±0,8º. Оценить точность конечного счислимого места.
Решение.
1. Определяем погрешности пути
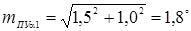 ,
,
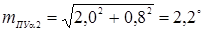 .
.
2. Используя табл. 4.1, рассчитываем средние квадратические погрешности счислимых мест Мn' через каждые 10 миль плавания, а затем определяем Мn на все курсы плавания. Входными аргументами в табл. 4.1 являются mПУa и mDл; M1' = 0,368; М1 = 0,368 · 2,5 = 0,92 мили = 9,2 кб; М'2 = 0,416; М2 = 0,416 · 1,5 = 0,624 мили = 6,2 кб.
3. Вычисляем радиус круга погрешности Мс конечного счислимого места (необходимо учесть и точность начальной точки счисления, так как по условию М0 не равно нулю):
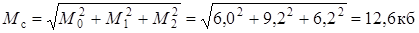 .
.
4. С помощью циркуля очерчиваем окружность радиусом 12,6 кб
(1,3 мили), в пределах которой с вероятностью 63 ¸ 68 % находится место судна.
Образец заполнения расчетной таблицы и оформления прокладки при ведении графического счисления с учетом дрейфа указаны в приложении 9.
Дата добавления: 2019-05-21; просмотров: 952;











