ПРИЛОЖЕНИЕ И. Лобовое столкновение тяжелой частицы с электроном

Рассмотрим лобовое столкновение быстрой (но нерелятивистской) тяжелой частицы с массой m_a и кинетической энергией T₀ c покоящимся (в лабораторной системе координат) электроном. Обозначив как p₀ импульс тяжелой частицы до столкновения, запишем законы сохранения энергии и импульса в рассматриваемой системе в общем виде:

,

,

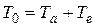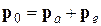где индексы а и е относятся к тяжелой частице и электрону после столкновения соответственно. Так как после столкновения обе частицы будут двигаться в направлении движения тяжелой частицы, последнее равенство можно записать в скалярной форме как

.

Предположим, что энергия T_e, преданная электрону, мала по сравнению с его энергией покоя. В этом случае классическая связь между кинетической энергией и импульсом дает

,

или, после алгебраических преобразований,

.

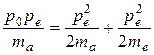Так как масса электрона много меньше массы тяжелой частицы, то первым слагаемым правой части по сравнению со вторым можно пренебречь. Тогда после сокращения на p_e получим

.

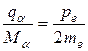Выразив импульс тяжелой частицы через ее скорость v_a, найдем, что импульс электрона

,

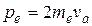а его кинетическая энергия

.

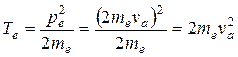Определим теперь условие, при котором характер движения электрона можно считать классическим. Для этого выразим кинетическую энергию электрона через начальную кинетическую энергию тяжелой частицы:

,

откуда

.

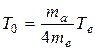Релятивистские эффекты становятся существенными, если кинетическая энергия электрона составляет ~10% от его энергии покоя m_ec² = 0,511 МэВ. Так как электрон легче нуклона примерно в 1820 раз, движение электрона будет подчиняться законам классической механики, если тяжелая частица представляет собой протон с кинетической энергией T₀ < 23 МэВ, ядро ⁴Не с энергией < 93 МэВ, и т.д.