Модель окисления кремния Дила-Гроува

Методом радиоактивного маркера показано, что рост SiO₂ происходит за счет диффузии кислорода к поверхности кремния. Выход SiO₂ за границы начального объема, занимаемого кремнием, обусловлен их разными плотностями.

Для теоретического обоснования было предложено множество моделей, основанных на объемной диффузии заряженных частиц или нейтральных пар, а также эффектах туннелирования электронов, кинетике адсорбции, образования пространственного заряда, изменении граничных концентраций диффундирующих частиц в зависимости от толщины пленки и многих других.

К сожалению, ни один из указанных механизмов не способен полностью объяснить обширный класс имеющихся к настоящему времени экспериментальных данных. Что касается получения пленок двуокиси кремния, то кинетику ее роста в широком диапазоне толщин SiO₂ можно объяснить, исходя из достаточно простой модели Дила-Гроува(см. рис).

Процесс окисления происходит на границе Si - SiO₂, поэтому молекулы окислителя диффундируют через все предварительно сформированные слои окисла и лишь затем вступают в реакцию с кремнием на его границе. Согласно закону Генри, равновесная концентрация твердой фазы прямо пропорциональна парциальному давлению газа P:

C* = HP, где

• C* - максимальная концентрация окислителя в газе для данного значения давления P,
  H - постоянный коэффициент Генри.

В неравновесном случае концентрация окислителя на поверхности твердого тела меньше, чем C*.

Поток F1 определяется разностью между максимальной и реальной поверхностной концентраций окислителя:

F1 = h(C* - C0), где

• C₀ - поверхностная концентрация окислителя,
  h - коэффициент переноса.

Значение концентрации окислителя C0 зависит от температуры, скорости газового потока и растворимости окислителя в SiO₂.

Для того чтобы определить скорость роста окисла, рассмотрим потоки окислителя в объеме окисла F2 и на его границе с кремнием F3. Согласно закону Фика, поток через объем окисла определяется градиентом концентрации окислителя:

F2 = - D(dC/dz) = D(C0 - Ci)/z₀, (1)

• где C_i - концентрация окислителя в молекулах на кубический сантиметр при z = z₀,
  D - коэффициент диффузии при данной температуре,
  z₀ - толщина окисла.

Величина потока F3 на границе окисла с полупроводником зависит от постоянной K скорости поверхностной реакции и определяется как:

F₃= kCi (2)

При стационарных условиях эти потоки равны, так что F3 = F2 = F1 = F.Следовательно, приравняв соотношения (1) и (2), можно выразить величины Ci и C0 через C*:

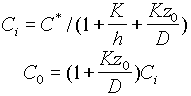(3)

Для того чтобы определить скорость роста окисла, представим поток F3 как изменение числа молекул в слое dz₀ за время dt. Тогда уравнение потока на границе SiO₂ - Si будет иметь следующий вид:

(4)

Скорость роста окисла определяется потоком F3 и количеством молекул окислителя Ni, входящих в единичный объем окисла. Поскольку концентрация молекул SiO₂ в окисле равна 2.2·10²² см^-3, то для получения двуокиси кремния требуется такая же концентрация молекул кислорода или в два раза большая концентрация молекул воды.

Соотношение между величинами z₀ и t определяется интегралом вида

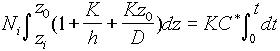(5)

В результате интегрирования получаем

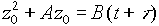(6)

где 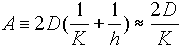(т.к. обычно h >> D), ,

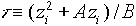, z_i=20 нм для сухого O₂, z_i=0 нм для влажного O₂,

z_i - начальное значение толщины окисла при t=0.

Решая уравнение (6) для значения толщины окисла z₀, получаем

(7)

Уравнение (7) упрощается и приводится к виду